车站是奇数个，两边的车才会同时到达

为了便于分析，我们做一些合理的假设。

汽车走过一站路时间相同。

汽车间隔相同的时间同时从两个终点站开出。

首先考虑最简单的情况，即汽车每走过一站，两个终点就发车。不难想象在这种情况下，公交系统开始运行一段时间后，每次只要有一辆车停站，所有车都会停站。

如此一来，当你在站台看到对面的汽车缓缓进站时，也就意味着这边反向的车也同时到达了。

然而，实际情况并非如此。不堵车时公交走过一站的平均时间大约是2.5分钟，而发车间隔时间最少为5分钟。那此时的情况又会是什么样呢？

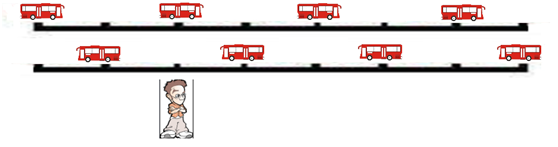
很显然，对面的2路汽车进站后，这边的车在2.5分钟后才能到来。

可是，如果站总数是奇数，情况又不一样。

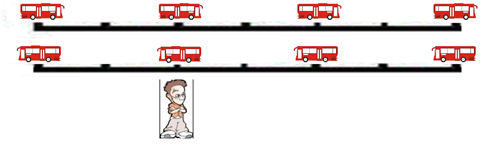
也就是说，车站是奇数个时，那个说法仍然成立。可如果是偶数，当对面的公交车到来时，你还得等两分半钟。

汽车运行时间不同，等待时间也不同

但如果发车间隔和车走一站的时间不是简单的2倍关系，又会发生什么呢？这里用Matlab编了一个小程序，得到了下面的图。

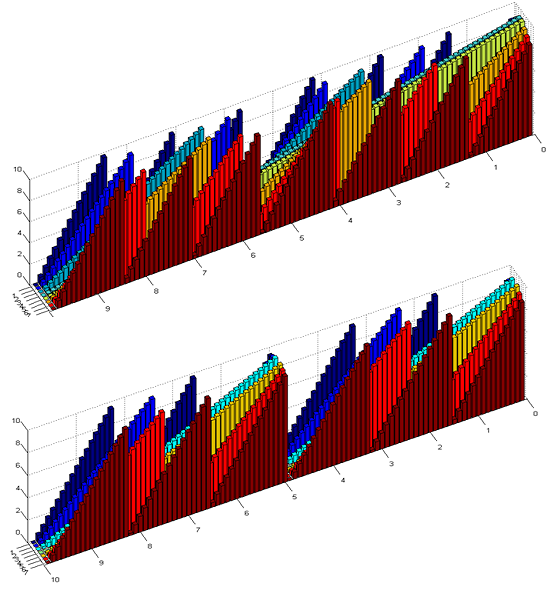
上面两个图表示的是车站(不包括起点和终点)分别为偶数个(8个)和奇数个(7个)，发车间隔10分钟时，车走完一站时间(下文用t表示)不同(从 0.1 分钟到 9.9 分钟)情况下，对面车来了之后仍需要的等待时间。

可以看出，除了车站为奇数正中的那个站之外，任何一个车站在t变化时，等车时间都会经历从0到接近10分钟的震荡变化，且越靠近始发和终点站，这种变化越明显。比如对于上面的图，第一站的等待时间变化一个周期，需要车走完一站时间t变化接近2分钟，而第二站则需要 3.5 分钟，第三站则是 5 分钟。换句话说，越靠近两边，车站等候时间对车走完一站的时间的变化就越敏感。

现实中，对面车来了：和你没关系

现实情况中，车站总数往往超过 20 个，此时两边的车站上看见对面来车后等到车所需的时间随车走一站的时间变化会更敏感。下面这个图表示了 20 个(红线)和 8 个(蓝线)车站(不算始发站和终点站)的情况下，第 1 个车站那里对面来车后需要等待的时间随t的变化趋势。默认终点站的公交车车对开间隔10分钟。在车站数到达 20 个时，t只要变化 0.5 分钟，等待时间就从将近十分钟变为几乎同时开来。而只有 8 个车站时，经历这样的1个周期则t就变化了1分40秒。

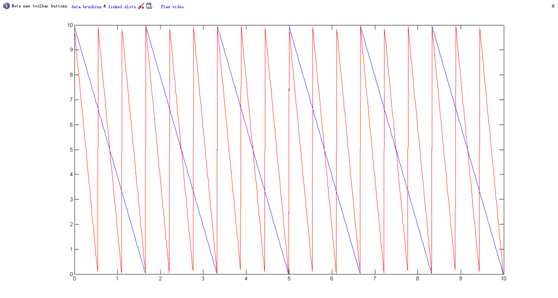
很自然的，你会问：在这种情况下，如果车走过一站的时间不确定，那么会不会对面开过来车以后需要等的时间的分布更倾向于比较小的数字呢？

为此，我们假设这样的情景：总共 19 个(或 20 个)车站(不包括始发和终点)，每隔十分钟发一趟车，车走过一站的时间满足正态分布(均值为 2.5 , 标准差 0.5 )。利用 Matlab 生成 1000 个满足正态分布的伪随机数用来代表t，再根据上文的那个小程序，就能得到对应于每一站的对面来车后需要等待的时间。结果如下。

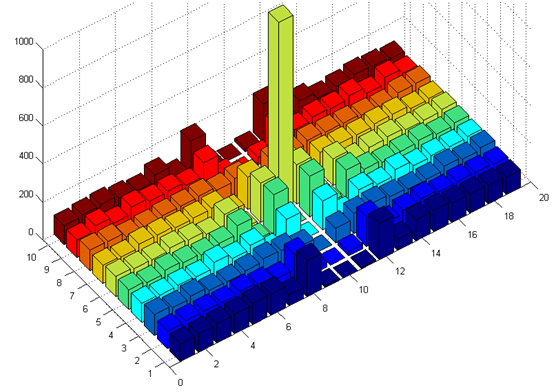
总车站为19时对应于每个车站等车时间的概率分布

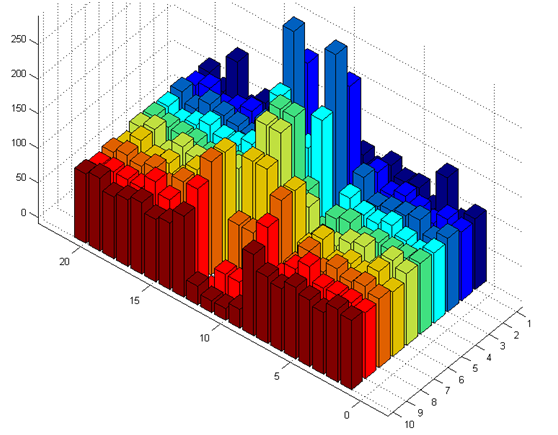
总车站为20时对应于每个车站等车时间的概率分布

可见，对于以上两种情况，除了最中间部分的车站外，在其他每个车站的等待时间都是 0 到 10 的均匀分布。也就是说，认为等待时间不存在或者很小的说法是错的。当然，注意到第 2 种情况下离中间两个车站最近的 2 个站上，确实出现了 3 分钟之内来车概率更高的现象(约 60% )，但这只是一个特例。

总而言之，下次再在车站等车时，可以忽略对面是否来车，因为它根本不能表明这边的车也快来了。