折纸几何公理

1991 年，日裔意大利数学家藤田文章（Humiaki Huzita） 指出了折纸过程中的 6 种基本操作，也叫做折纸几何公理。假定所有折纸操作均在理想的平面上进行，并且所有折痕都是直线，那么这些公理描述了通过折纸可能达成的所有数学操作：

1. 已知 A 、 B 两点，可以折出一条经过 A 、 B 的折痕

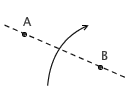
2. 已知 A 、 B 两点，可以把点 A 折到点 B 上去

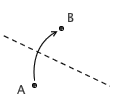
3. 已知 a 、 b 两条直线，可以把直线 a 折到直线 b 上去

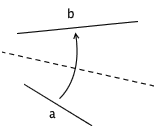
4. 已知点 A 和直线 a ，可以沿着一条过 A 点的折痕，把 a 折到自身上

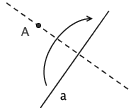
5. 已知 A 、 B 两点和直线 a ，可以沿着一条过 B 点的折痕，把 A 折到 a 上

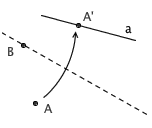
6. 已知 A 、 B 两点和 a 、 b 两直线，可以把 A 、 B 分别折到 a 、 b 上

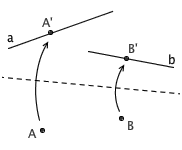
容易看出，它们实际上对应着不同的几何作图操作。例如，操作 1 实际上相当于连接已知两点，操作 2 实际上相当于作出已知两点的连线的垂直平分线，操作 3 则相当于作出已知线段的夹角的角平分线，操作 4 则相当于过已知点作已知线的垂线。真正强大的则是后面两项操作，它们确定出来的折痕要满足一系列复杂的特征，不是尺规作图一两下能作出来的（有时甚至是作不出来的）。正是这两个操作，让折纸几何有别于尺规作图，折纸这门学问从此处开始变得有趣起来。

更有趣的是，操作 5 的解很可能不止一个。在大多数情况下，过一个点有两条能把点 A 折到直线 a 上的折痕。

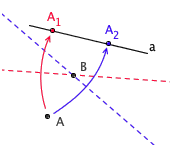
操作 6 则更猛：把已知两点分别折到对应的已知两线上，最多可以有三个解！

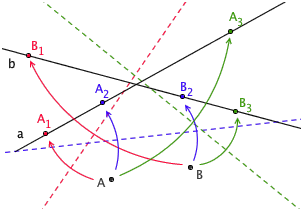
一组限定条件能同时产生三个解，这让操作 6 变得无比灵活，无比强大。利用一些并不太复杂的解析几何分析，我们能得出操作 6 有三种解的根本原因：满足要求的折痕是一个三次方程的解。也就是说，给出两个已知点和两条对应的已知线后，寻找符合要求的折痕的过程，本质上是在解一个三次方程！

尺规作图到底局限在哪里

相比于折纸的几何操作，尺规作图就显得有些不够“强大”了。不妨让我们先来回顾一下尺规作图里的五个基本操作：

过已知两点作直线

给定圆心和圆周上一点作圆

寻找直线与直线的交点

寻找圆与直线的交点

寻找圆与圆的交点

这5项操作看上去变化多端，但前3项操作都是唯一解，后两项操作最多也只能产生两个解。从这个角度来看，尺规作图最多只能解决二次问题，加减乘除和不断开方就已经是尺规作图的极限了。能解决三次问题的折纸规则，势必比尺规作图更加强大。

正因为如此，一些尺规作图无法完成的任务，在折纸几何中却能办到。比如折纸法可以实现作正七边形，而这是无法用尺规作图办到的。

我们有更简单的例子来说明，用折纸法能完成尺规作图办不到的事情。“倍立方体”问题是古希腊三大尺规作图难题之一，它要求把立方体的体积扩大到原来的两倍，本质上是求作 2 的立方根。由于尺规作图最多只能开平方，因而它无法完成“倍立方体”的任务。但是，折纸公理 6 相当于解三次方程，解决“倍立方体”难题似乎是游刃有余。

有意思的是，用纸片折出 2 的立方根比想象中的更加简单。取一张正方形纸片，将它横着划分成三等份（方法有很多，大家不妨自己想想）。然后，将右边界中下面那个三等分点折到正方形内上面那条三等分线上，同时将纸片的右下角顶点折到正方形的左边界。那么，纸片的左边界就被分成了 3√2 : 1 两段。

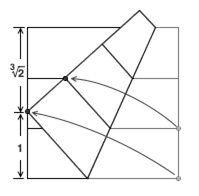
利用勾股定理和相似三角形建立各线段长度的关系，我们不难证明它的正确性。强烈建议大家自己动笔算一算，来看看三次方程是如何产生的。

第7个折纸公理

本文写到这里，大家或许以为故事就结束了吧。 10 年以后也就是 2001 年，事情又有了转折： 数学家羽鳥公士郎（Koshiro Hatori）发现，上述的 6 个折纸公理并不是完整的。 他给出了折纸的第 7 个定理。从形式上看，第 7 公理与已有的公理如出一辙，并不出人意料，很难想象这个公理整整十年里竟然一直没被发现。继续阅读之前，大家不妨先自己想想，这个缺失的操作是什么。这段历史背景无疑让它成为了一个非常有趣的思考题。

补充的公理是：

7. 已知点 A 和 a 、 b 两直线，可以沿着一条垂直于 b 的折痕，把 A 折到 a 上。

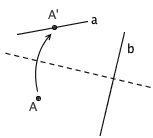
后来，这 7 条公理就合称为了藤田－羽鳥公理（Huzita–Hatori 公理），你可以在 维基百科 上读到这个条目。在 2003 年的一篇文章中，世界顶级折纸 艺术家 罗伯特•朗 （Robert J. Lang ）对这些公理进行了一番整理和分析，证明了这 7 条公理已经包含折纸几何中的全部操作了。

看，艺术家都是先搞数学的！

罗伯特•朗注意到，上述 7 项基本操作其实是由一些更基本的操作要素组合而成的，例如“把已知点折到已知线上”、“折痕经过已知点”等等。说得更贴切一些，这些更加基本的操作要素其实是对折痕的“限制条件”。在平面直角坐标系中，折痕完全由斜率和截距确定，它等价于一个包含两个变量的方程。不同的折叠要素对折痕的限制力是不同的，例如“把已知点折到已知点上”就同时要求 x1' = x2 并且 y1' = y2 ，可以建立出两个等量关系，一下子就把折痕的两个变量都限制住了。而“折痕经过已知点”则只能列出一个方程，只能确定一个变量（形式上通常表示为与另一个变量的关系），把折痕的活动范围限制在一个维度里。

不难总结出，基本的折叠限制要素共有 5 个：

(1) 把已知点折到已知点上，确定 2 个变量

(2) 把已知点折到已知线上，确定 1 个变量

(3) 把已知线折到已知线上，确定 2 个变量

(4) 把已知线折到自身上，确定 1 个变量

(5) 折痕经过已知点，确定 1 个变量

而折痕本身有 2 个待确定的变量，因此符合要求的折纸操作只有这么几种： (1) ， (2) + (2) ， (3) ， (4) + (4) ， (5) + (5) ， (2)+(4) ， (2) + (5) ， (4) + (5) 。但是，这里面有一种组合需要排除掉： (4) + (4) 。在绝大多数情况下， (4) + (4) 实际上都是不可能实现的。如果给出的两条直线不平行，我们无法折叠纸张使得它们都与自身重合，因为没有同时垂直于它们的直线。

另外 7 种则正好对应了前面 7 个公理，既无重合，又无遗漏。折纸几何至此便有了一套完整的公理。

不过，折纸的学问远远没有到此结束。如果允许单次操作同时包含多处折叠，折纸公理将会更复杂，更强大。折纸的极限究竟在哪里，这无疑是一个非常激动人心的话题。

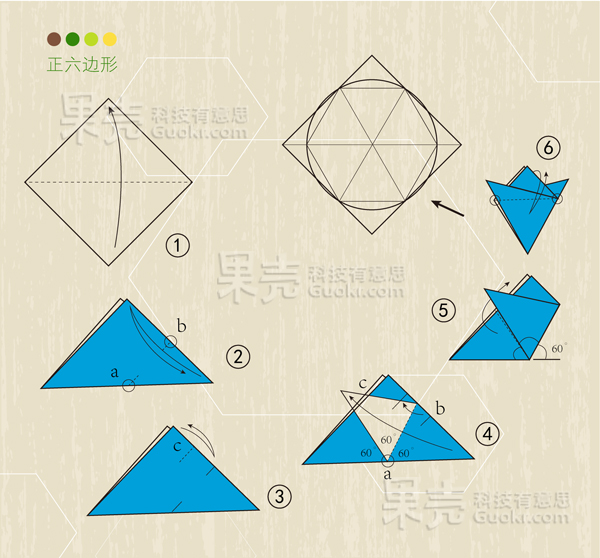
在这里，简单展示几个折纸几何学的例子，分别是三等分角、黄金比例和正六边形。图片由果壳美术设计师 V晶V 制作

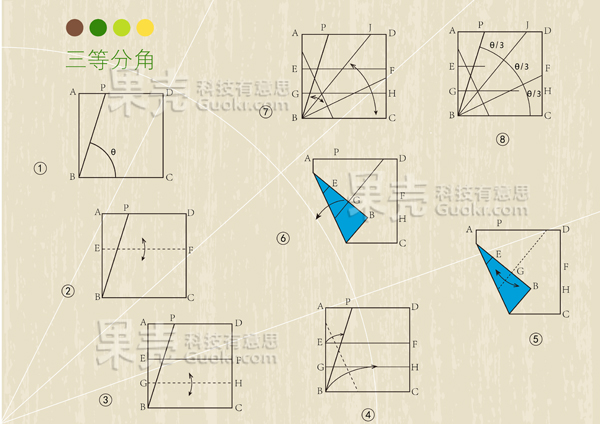
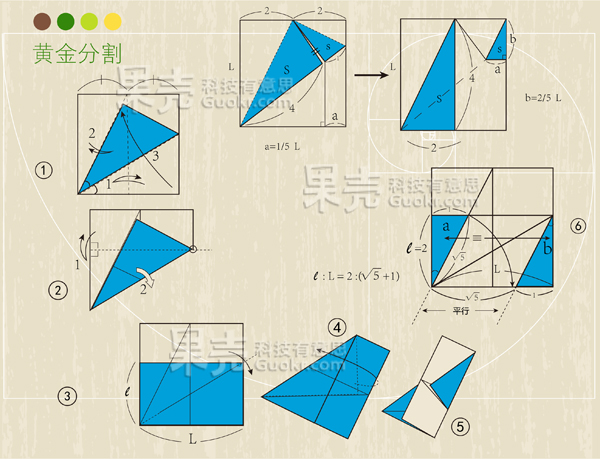
相关阅读：

“叹为观纸”第一期：现代折纸介绍

折纸戢戢然，算法苏苏然

折纸又见折纸