关联规则的常用解法
Apriori 算法
Apriori算法是一种最有影响的挖掘 0-1 布尔关联规则频繁项集的算法。这种算法利用了频繁项集性质的先验知识(因此叫做priori)。Apriori使用了自底向上的实现方式(如果集合 I 不是频繁项集,那么包含 I 的更大的集合也不可能是频繁项集),k - 1 项集用于探索 k 项集。首先,找出频繁 1 项集的集合($L_1$),$L_1$用于找频繁 2 项集的集合 $L_2$,而 $L_2$ 用于找 $L_3$,如此下去,直到不能找到满足条件的频繁 k 项集。搜索每个 $L_k$ 需要一次全表数据库扫描。
我们假设一个很小的交易库:{1,2,3,4}, {1,2}, {2,3,4}, {2,3}, {1,2,4}, {3,4}, {2,4}
首先我们先要计算发生频数(或者叫做support)
| item | support | |
|---|---|---|
| {1} | 3| | |
| {2} | 6| | |
| {3} | 4| | |
| {4} | 5| |
1项集的最低频数是3,我们姑且认为他们都是频繁的。因此我们找到1项集所有可能组合的pairs:
| item | support | |
|---|---|---|
| {1,2} | 3| | |
| {1,3} | 1| | |
| {1,4} | 2| | |
| {2,3} | 3| | |
| {2,4} | 4| | |
| {3,4} | 3| |
在这里,{1,3}, {1,4} 不满足support大于3的设定(一般support是3/(3 + 6 + 4 + 5)),因此还剩下的频繁项集是:
| item | support | |
|---|---|---|
| {1,2} | 3| | |
| {2,3} | 3| | |
| {2,4} | 4| | |
| {3,4} | 3| |
也就是说,包含{1,3}, {1,4}的项集也不可能是频繁的,这两条规则被prune掉了;只有{2,3,4} 是可能频繁的,但它的频数只有2,也不满足support条件,因此迭代停止。
但我们可以想象,这种算法虽然比遍历的方法要好很多,但其空间复杂度还是非常高的,尤其是 $L_1$ 比较大时,$L_2$ 的数量会暴增。而且每次Apriori都要全表扫描数据库,开销也非常大。
即便如此apriori算法在很多场景下也足够用。在R语言中使用arules包来实现此算法(封装的是C实现,速度很快噢)
FP growth
前文提到了用apriori需要全表扫描,对于超大型数据会出现一些问题。如果有一种方法,可以不每次全表扫描,而是用一个简洁的数据结构(条件数据库)把整个数据库的信息都包含进去,通过对数据结构的递归就完成整个频繁模式的挖掘,并保证最低的搜索消耗。这种方法就是FP growth算法。这个算法因为数据结构的 size 远远小于原始的数据库,所有的数据操作可以完全在内存中计算,挖掘速度就可以大大提高。
FP growth 算法包含两部分:存储的FP tree 和对应的FP 算法:
FP-tree 的结构
J. Han 对 FP-tree 的定义如下:
- 根节点被标记为 root,item 按照一定的顺序连接为子树。以及一个frequent-item-header 表(其实就是item按照出现频率排序的表格,下图中左侧的表格)
- 每个子树上包含如下信息:
- item 的名称(比如下图中I2, I3, I5等)
- 计数(support count):到达这个节点的路径深度
- 节点的连接情况(node-link,和哪个节点有关系)
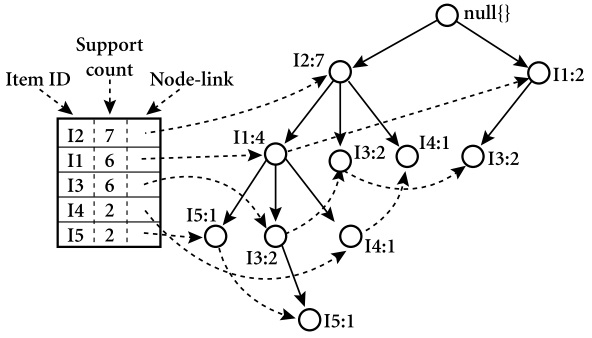
FP-tee 的算法
我们拿一个例子来说明问题。假如我们数据库中记录的交易信息如下(最低support为3):
| No. | transactions | Sort | |
|---|---|---|---|
| 1 | ABDE | BEAD| | |
| 2 | BCE | BEC| | |
| 3 | ABDE | BEAD| | |
| 4 | ABCE | BEAC| | |
| 5 | ABCDE | BEACD| | |
| 6 | BCD | BCD| |
首先我们先要了解所有的一项集出现的频率(support,重新排序的结果见上图的Sort部分):B(6), E(5), A(4), C(4), D(4)。
对于排序后的每条记录的迭代后 FP-tree 结构变化过程为(也就是一条一条计数的增加):
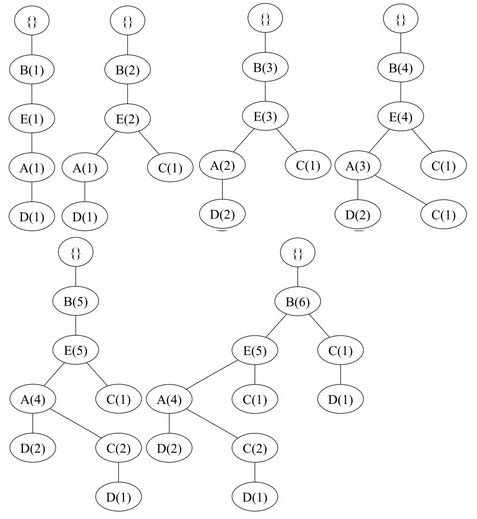
也就是说,原始数据被压缩到和最后那张图一样的结构上。
接着是比较关键的 FP-tree 的挖掘,过程见下图:
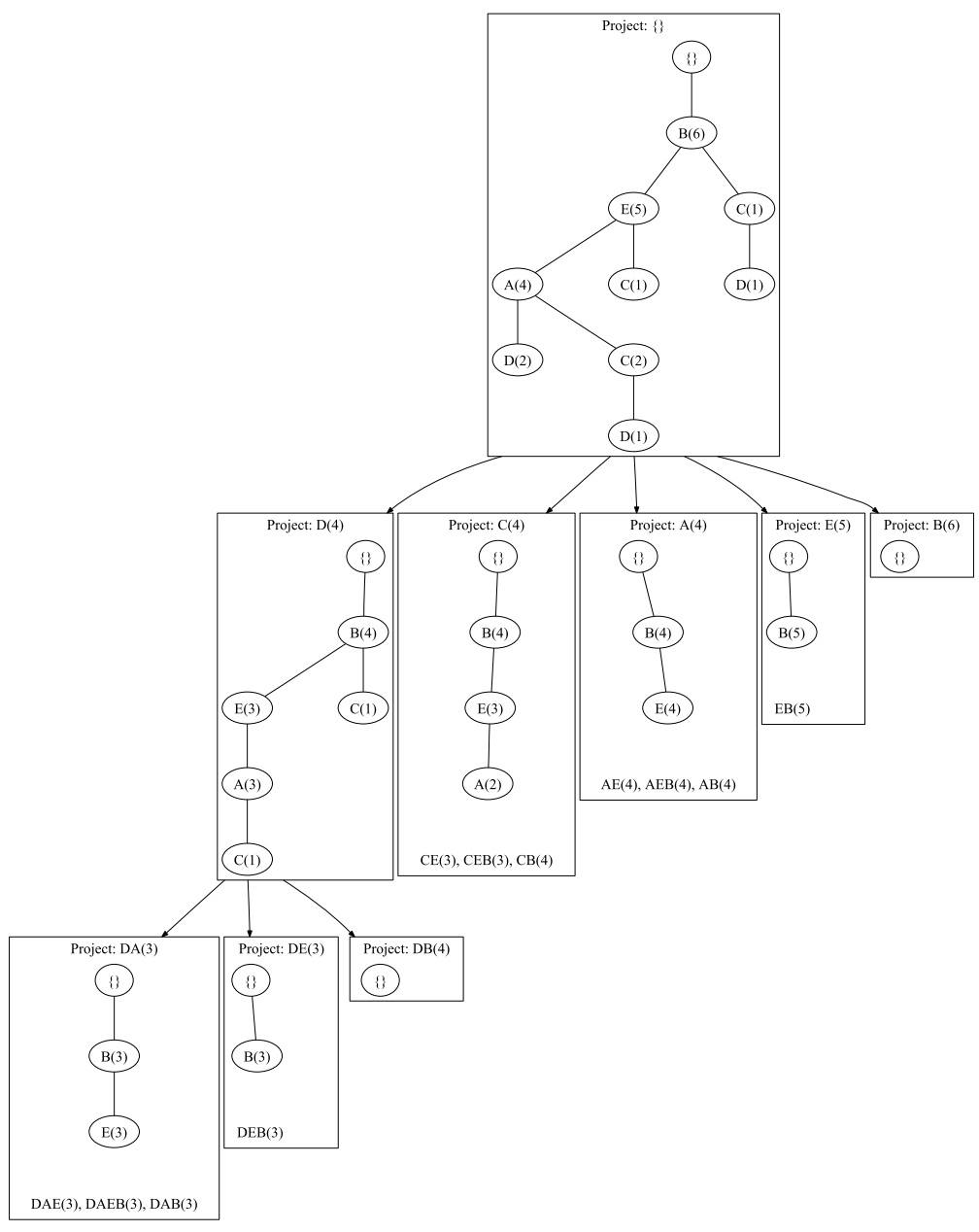
对于D这个节点来说,首先它的频繁项集是 $D(4)$,它包含在三条链路里:
$ ( B(6),E(5),A(4) ), ( B(6),E(5),A(4),C(2) ), ( B(6),C(1) ) $
第一条链路里D有两次出现,而其他两个链路在D的条件下各出现了一次。因此我们说D有3个前缀路径
$ (BEA:2),(BEAC:1),(BC:1) $
根据这个信息我们重构D条件下的 FP-tee,则如下图中 $Project:D(4)$ 的结构。当然还没有完,还要继续搜索可能的规则,因为我们的 support 为3,因此 $Project:D(4)$ 中,最末端的两个 $C(1)$ 则应该减枝掉。而A、E、B的频数依然可以被使用,即 $DA(3)、DE(3)、DB(4)$。
- 对于 $DA(3)$ 的前缀路径是 $Project:DA(3)$ 的树形结构,因此这条线的最终结果是 $DAE(3),DAEB(3),DAB(3)$。
- 对于 $DE(3)$ 的前缀路径是 $Project:DE(3)$ 的属性结构,最终结果是 $DEB(3)$
- 对于 $DB(4)$ 只有一个根,没有结果
对于C这个节点来说,同样可以找到它的前缀路径 $(BEA:2),(BE:1),(B:1)$,因此得到 $Project:C(4)$ 的结构,A被减枝掉,则最后剩余了 $CE(3),CEB(3),CB(4)$。
再向上,找A节点;找E节点;找B节点;这样一步一步搜索所有可能的结果。最终满足support大于3条件的频繁项集即为 $ DAE, DAEB, DAB, DEB, CE, CEB, CB, AE, AEB, AB, EB $
当然,上面只是简单的把 FP-tree 的原理说明了一下,里面的一些trick并没有提及,感兴趣的读者可以找一找相关paper。
FP-tree 算法在R中的实现
在R中没有现成的包来做这个事情,但有意思的是arules包的作者也写了 FP-tree 算法,只是没有封装而已。当然只要有算法的C代码,嵌入到R环境中也是不难的。
先到作者的主页下载相关的 源代码,我选择是的fpgrowth.zip的C代码编译通过。
cd /home/liusizhe/download/fpgrowth/fpgrowth/src/
make
make install
./fpgrowth -m2 -n5 -s0.075 /home/liusizhe/experiment/census.dat frequent
参数的话,可以直接参考fpgrowth的帮助,比如上面m对应的是最小项集,n对应的最大项集,s是support值