ComSec概念概述
ComSec总结
这学期选修了bintou老师的ComSec计算机安全课,上课期间觉得自己学的马马虎虎的,学习了一些计算机安全中的密码学算法和安全概念,但对这些概念都不是特别清晰,期末复习的过程中,对其中的一些算法和概念更理解了一些,趁着刚考完还没忘记,总结一波挂在博客,不当之处,欢迎指正。
公钥密码学概述
公钥密码学也称为 非对称密码学,与传统的对称密码学区别在于,加密和解密使用 不同的密钥,也就是所说的 key,其中公开出来的密钥是 公钥,另一个是私钥,由持有者 严格保密。且 公钥密码是基于数学函数而不是基于替换和置换。
公钥密码学提出的解决的基本问题包括有
- 密钥交换
- 数字签名
公钥密码的六个组成成分分别是 明文, 密文, 公钥, 私钥, 加密算法, 解密算法。
公钥密码的重要特点是
- 仅根据密码算法和加密密钥,确定解密密钥在 计算上不可行,所谓计算上不可行即是
解决一个问题所需要的时间比输入规模的多项式增长更快,如输入长度为n位,计算复杂度是2n2^{n}2n。 - 两个密钥中的任意一个都可用来加密,另一个用来解密,也就是说,存在两个方式,一种是
公钥加密,私钥解密,一种是私钥加密,公钥解密。根据这两种方式,公钥密码体制分成了两个模式,一个是 加密模式,一个是 认证模式。
加密模式
所谓 加密模式,也就是用 公钥加密,私钥解密的模式。
加密模式的运行过程如下,A向B发消息X,已知B的公钥为KUbK_{Ub}KUb,私钥为KRbK_{Rb}KRb,加密算法为E,解密算法为D,则加密过程为Y=EKUb(X)Y=E_{K_{Ub}}(X)Y=EKUb(X),解密过程X=DKRb(Y)X=D_{K_{Rb}}(Y)X=DKRb(Y)。之所以能够保证 传递消息是保密的,是因为只有 私钥才可以解密,而私钥只有B持有。所以所有想给B发消息的人,只需要用B的公钥和对应的加密算法对消息进行加密即可,而加密的消息只有B能解,保证了 消息的保密性。
认证模式
所谓 认证模式,也就是用 私钥加密,公钥解密的模式。
认证模式的运行过程如下,A向B发消息,已经A的公钥为KUaK_{Ua}KUa,A的私钥为KRaK_{Ra}KRa,加密算法为E,解密算法为D,则加密过程为Y=EKRa(X)Y=E_{K_{Ra}}(X)Y=EKRa(X),解密过程为X=DKUa(Y)X=D_{K_{Ua}}(Y)X=DKUa(Y),注意这里虽然说的是加密算法和解密算法,但是 认证模式下并不能保证消息的保密性,因为只要知道A的公钥的人就可以解出明文,而公钥又是公开的,所以并不能提供消息的保密性,那么认证模式是来干嘛的呢?认证模式 只有私钥能加密,借助这个 唯一加密的特性,可以实现数字签名,私钥就相当于你的 字迹,别人无法模仿的,别人一看到这个字迹就知道是你写的,就相当于别人用公钥验证私钥,验证成功,知道消息是你发的,提供了 认证性。
同时具有保密与认证的公钥体质
那么如果我们传送消息时,想要同时有 加密和 认证两种需求,如何做呢?很简单,就是用两对公私钥对,一对采用 加密模式,一对才用 认证模式。
假定A向B发消息,A的密钥对为{KUaK_{Ua}KUa,KRaK_{Ra}KRa},B的密钥对为{KUbK_{Ub}KUb,KRaK_{Ra}KRa},A要求发的消息同时具有 加密性和 认证性,怎么做呢?
首先是加密性,加密性需要用 公钥加密,私钥解密,用谁的公钥呢?B的,因为B要查看消息,所以B要用自己的私钥去解密消息,所以A就用B的公钥去加密要传送的消息。 认证需要用私钥加密,用谁的私钥呢?A的,因为B要确认消息是A所发出的,所以用A的私钥对消息进行加密,B收到消息后用解密算法进行验证,实现认证。
整个过程如下:假定发送的 明文为X
首先用B的公钥对消息进行加密Z=EKUb(X)Z=E_{K_{Ub}}(X)Z=EKUb(X),这一步实现的是 加密,然后再执行Y=EKRa(Z)Y=E_{K_{Ra}}(Z)Y=EKRa(Z),这一步实现的是 认证,然后将密文Y传送给B,B收到Y后首先做Z=DKUa(Y)Z=D_{K_{Ua}}(Y)Z=DKUa(Y)解出Z,然后执行X=DKRb(Z)X=D_{K_{Rb}}(Z)X=DKRb(Z)解出明文X,实现了 加密和 认证。
公钥密码体制应满足的要求
公钥密文体制的运行也需要一些要求
一般要求:
- 加密解密算法相同,但使用密钥不同
- 发送方拥有加密或解密密钥,而接收方拥有另一个密钥。
安全性要求:
- 两个密钥之一必须保密, 作为私钥
- 无解密密钥,解密不可行
- 知道算法和其中一个密钥,以及若干个密文不能确定另一个密文。
关于公钥密码的几种误解
-
公钥密码比传统密码更安全?
任何加密算法的 安全性依赖于 密钥的长度和 破译密文所需要的计算量。从抗密码分析的角度来看,原则上不能说传统密码优于公钥密码,而不能说公钥密码优于传统密码。
-
公钥密码是通用方法,所以传统密码已经过时?
其实恰恰相反,由于现有的公钥密码方法所需的 计算量大,取缔传统密码似乎不太可能,仅限用在 密钥管理和 签名这类应用上。
-
公钥密码实现密钥分配非常简单?
事实上,使用公钥密码也需要某种形式的 协议,该协议通常包含一个 中心代理,并且它的处理过程也不比传统密码中的那些过程简单和有效。
RSA
RSA公开密钥密码体制是最著名且被广泛使用的公开密钥密码体制。
RSA算法的基本过程
首先,明文和密文是0~n-1之间的整数,通常n的大小为1024位或309位十进制。
RSA算法描述
加密:C=Me mod NC=M^{e} \ mod \ NC=Me mod N where 0<= M < N
解密:$M=C^{d} mod \ N \ $
公钥为(e,N),私钥为(d,N)。
必须满足的以下条件
-
Med≡M mod NM^{ed} ≡ M \ mod \ NMed≡M mod N
-
计算MeM^{e}Me和CdC^{d}Cd是比较容易的( 效率)。
-
由e和n确定d是不可行的( 安全)。
密钥产生过程
-
随机选择两个不等的 大素数p,q
-
计算N=p*q,对应有ϕ(N)=(p−1)×(q−1)\phi(N)=(p-1)×(q-1)ϕ(N)=(p−1)×(q−1)
-
选择e使得 1<e<ϕ(N)1<e<\phi(N)1<e<ϕ(N),且$gcd(e,\phi(N)) = 1 (使得e在(使得e在(使得e在\phi(N)$下存在 逆元,也就是后面我们要求的d)
-
解下列方程求出d
ed≡1 mod ϕ(N)ed ≡ 1 \ mod \ \phi(N)ed≡1 mod ϕ(N) 且 0<= d <= N
-
公布公钥KU={e,N}
-
保存私钥KR={d,N}
RSA的使用
- 发送方加密明文M
- 获取接收方的公钥KU={e,N}
- 计算$C=M^{e} \ mod \ N $ where 0<= M < N
- 接收方解密密文C
用自己的私钥KR={d,N},计算 M=Cd mod NM=C^{d} \ mod \ NM=Cd mod N
为什么RSA可以加解密?
由 欧拉定理:
欧拉定理:设n和a为正整数,且gcd(a,n) = 1,则 aϕ(n)≡1 (mod n)a^{\phi(n)} ≡ 1\ (mod \ n)aϕ(n)≡1 (mod n)
又在RSA :ed≡1 mod ϕ(N)ed ≡ 1 \ mod \ \phi(N)ed≡1 mod ϕ(N),等价于ed=kϕ(N)+1ed=k\phi(N)+1ed=kϕ(N)+1
所以$M^{ed} ≡ M \ mod \ N $
等价于 Mkϕ(N)+1≡M mod NM^{k\phi(N)+1} ≡ M \ mod \ NMkϕ(N)+1≡M mod N
在RSA中 N=p×q,p,q为素数,所以有ϕ(N)=(p−1)×(q−1)\phi(N)=(p-1)×(q-1)ϕ(N)=(p−1)×(q−1)
且 ed≡1 mod ϕ(N)ed ≡ 1 \ mod \ \phi(N)ed≡1 mod ϕ(N)
因此,有Cd≡(Me)d=Med≡M mod N=MC^{d}≡ (M^{e})^{d}=M^{ed} ≡ M \ mod \ N = MCd≡(Me)d=Med≡M mod N=M
RSA密钥key的选择
从安全性考虑,key的选择需要以下规则
- p和q不能太接近
- p-1 和 q-1必须包含大的素因子
- gcd(q-1,p-1)必须小
- e和d不能太小,e可选65537
- d不能小于n1/4n^{1/4}n1/4
RSA的安全性
-
强力穷举攻击: 穷举所有可能的私钥
-
数学攻击:实质是对两个素数的乘积N的分解,由N求得ϕ(N)\phi(N)ϕ(N)是困难的,因此要将N分解为p和q两个质数,然后利用ϕ(N)=(p−1)∗(q−1)\phi(N)=(p-1)*(q-1)ϕ(N)=(p−1)∗(q−1)
-
时间攻击 :不懂
-
选择密文攻击CCA
三种数学攻击方法
-
分解N=p*q,由此可算出ϕ(N)\phi(N)ϕ(N),从而确定d
-
直接确定ϕ(N)\phi(N)ϕ(N),然后找到d
-
直接确定d
本质上都是要找到ϕ(N)\phi(N)ϕ(N)或直接找到d,由
N确定$\phi(N)$可等价于因子分解。
RSA公钥体质的安全性是建立在哪种事实之上?
因子分解具有大素数因子的数仍然是一个难题。
选择密文CCA
选择密文攻击是假定攻击者有一台 解密机,除了待解的密文,攻击者可以输入任意的密文,然后解密机就会给出对应的明文,因此攻击者可以构造特殊的密文,去求解出 待解的密文。
给定待解密文C∗C^{*}C∗,求对应的明文M∗M^{*}M∗,并给出一个解密机O
攻击过程:
构造密文C=2eC∗C=2^{e}C^{*}C=2eC∗
将C输入到解密机O,得到对应的明文M
M=(Cd mod N)=(2eC∗)d mod N=2edC∗d mod N=2∗m∗ mod N=2m∗M=(C^{d} \ mod \ N)=(2^{e}C^{*})^{d} \ mod \ N = 2^{ed}C^{*d} \ mod \ N = 2* m^{*} \ mod \ N = 2m^{*}M=(Cd mod N)=(2eC∗)d mod N=2edC∗d mod N=2∗m∗ mod N=2m∗
于是便可以求得m∗m^{*}m∗
Diffie-Hellman 密钥交换协议
Diffie-Hellman需要原根(生成元)的定义
原根:如果a是素数p的原根,则数 a mod p,a2 mod pa^{2} \ mod \ pa2 mod p … ap−1 mod pa^{p-1} \ mod \ pap−1 mod p是不同的并且包含1到p-1的整数的 某种排列。原根是数论的概念。
生成元:p为素数,g是Zp∗Z_{p}^{*}Zp∗的生成元,当且仅当g的阶是p-1. 生成元是 群论的概念。
Diffie-Hellman公钥体制
目标:Alice和Bob试图在公开网络上通过交互建立一个 秘密
Diffie-Hellman 密钥交换算法
全局公开量:
- 大素数:p
- 选g为Zp∗Z_{p}^{*}Zp∗的生成元
Alice密钥的产生:
选择随机数x<p
计算公开量 X=gx mod pX=g^{x} \ mod \ pX=gx mod p
Bob密钥的产生:
选择随机数y<p
计算公开量Y=gy mod pY=g^{y}\ mod \ pY=gy mod p
协议过程:
Alice -----> Bob:X
Bob -------> Alice:Y
产生密钥:
Alice接受到了Y,计算KAB=Yx mod qK_{AB}=Y^{x} \ mod \ qKAB=Yx mod q
Bob接受到了X,计算KAB=Xy mod qK_{AB}=X^{y}\ mod \ qKAB=Xy mod q
KAB=gxy mod qK_{AB}=g^{xy}\ mod \ qKAB=gxy mod q
这样双方就都计算出了密钥KABK_{AB}KAB,成功完成了密钥的交换,且 各自的私钥x和y没有暴露。
为什么没有暴露呢?因为传递的是X和Y,而Diffie-Hellman密钥的安全性正是建立在如下的事实上: 求关于素数的模幂运算相对容易,而计算离散对数问题却非常困难,对于大素数,求离散对数问题被认为是计算上不可行的
离散对数问题:给定y=gx mod py=g^{x} \ mod \ py=gx mod p,知道y,g,p,求x在计算上是不可行的,如果p是一个大素数
正因如此,双方才能在各自私钥不暴露的情况下完成密钥(KABK_{AB}KAB)的交换。
Diffie-Hellman算法中存在的问题
Diffie-Hellman算法中存在的问题就是 不能对抗中间人攻击。
中间人攻击原理如下:
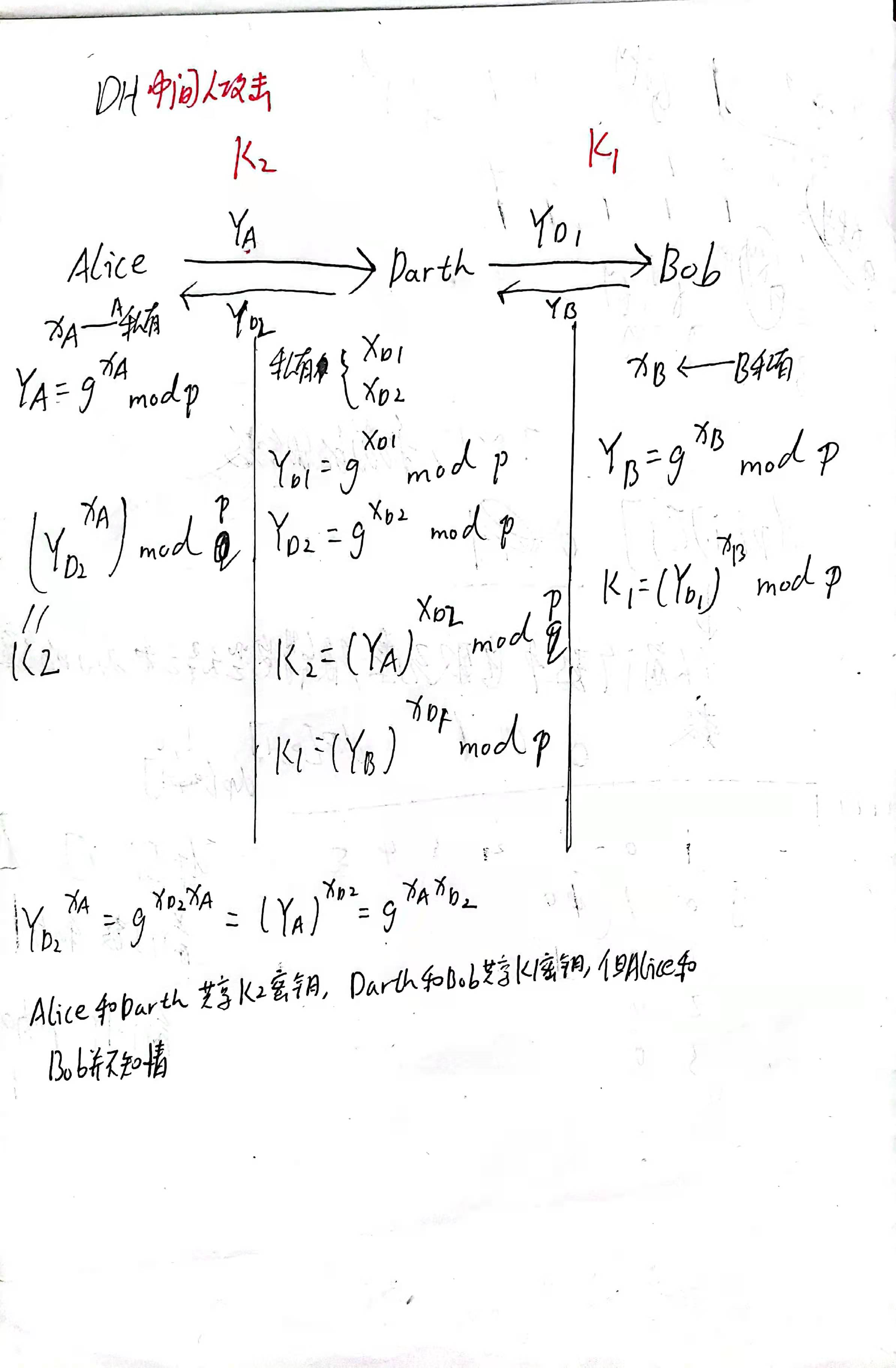
那么如何对抗中间人攻击呢?之所以存在中间人攻击,是因为Diffie-Hellman没有对通信的参与方 进行认证,所以引入 认证机制可以抵抗中间人攻击,如何引入 认证机制?就要用到我们前面提到的公钥密码的认证模式,具体的应用为 数字签名,通过添加 数字签名对通信的参与方进行认证,从而对抗中间人攻击。
ECC椭圆计算
只是一个只会在ZpZ_{p}Zp上计算的做题家罢了。
Hash与MAC部分
Hash函数:Hash函数不是加密解密函数,只是 保证消息的完整性,在密码学中具有重要的理论和应用价值。
Hash函数的定义
- Hash函数是将 任意长度的报文 映射成一个 较短的定长输出报文的函数。
- 如下形式 h=H(M),M是边长的报文,h是定长的Hash值。
- Hash函数的目的是为文件,报文或其他的分组数据产生 数字指纹,通过检查“数字指纹”判断消息有没有被篡改过,从而判断 消息的完整性。
对Hash函数的要求:
- 能用于任何大小的数据分组
- H产生定长输出
- 对任意给定的x,H(x)要相对 易于计算,使得软硬件实现都变得可行。
安全性需求:
-
单向性:对任意给定的码y,寻求x使得H(x)=y 在计算上不可行
-
弱抗碰撞性:任意分组x,寻求不等于x的x’,使得H(x)=H(x’) 在计算上不可行
-
强抗碰撞性:寻求任何的(x,x’),使得H(x)=H(x’) 在计算上不可行
密码学Hash函数的应用
-
消息认证:验证消息 完整性的一种机制或服务。确保收到的数据确实和发送时一样,即没有发生第三方截获了消息,进行修改,插入,删除或重放。此外,通常还要求消息认证机制确保" 发送方声称的身份是真实有效的",Hash函数用于提供消息认证功能时,Hash值也称为 消息摘要。更一般地,消息认证是通过 消息认证码MAC实现的,MAC即 带密钥的Hash。通信双方基于 共享的同一密钥来认证彼此交互的消息,就会使用MAC。
总体来看 MAC是 Hash函数和加密函数的集合,对Hash值保密,防止中间人篡改后轻松地 伪造Hash值。
-
数字签名:
Hash函数另一个重要的应用是 数字签名。数字签名的操作与MAC相似,但MAC防止是第三方的截获和篡改,而数字签名防止的是通信双方自己之间的欺骗( …全得防着,太可怕了)。在进行数字签名的过程中,使用用户的 私钥加密消息的Hash值,其他任何知道该用户 公钥的人都能够通过数字签名来 验证消息的完整性。
认证技术
认证是防止 主动攻击的重要技术,对开放系统的安全性起到重要作用。
认证的主要目的是:
一 实体认证( 发送者非冒充)
二 报文认证(验证消息的完整性)
报文认证MAC
报文认证,简单而言,就是要求接收方可以确保发送方发来的数据具有 真实性,没有被篡改或是伪造数据。
报文认证实例
- 在电子商务系统中,在电子政务系统中,我们需要确认某些电子文档不是伪造的。
- 在实际应用中,我们考虑如何把非法软件与合法软件区分开来。
特点:第三方可仲裁,离线或者非实时。
实体认证 – 用户认证
- 确保正在参与通信者是一个非冒充用户,比如QQ,MSN等即时通信系统,邮件系统等
- 实例:安全登录
- 特性:实时,在线,多方参与…
报文认证
Ailice与Bob共同拥有一个秘密sk,Alice用sk加密M给Bob,Bob解密,立即可知此报文是真假是假。但是这种方法无法防止Alice和Bob之间的相互欺骗,例如Alice否认自己发送过消息,因为Bob也可以伪造Alice给自己发消息,同时Bob也可以否认自己收过某条消息,问题的症状在于Alice与Bob共同拥有 私钥sk,而后的数字签名就是来解决这个问题的。
MAC的安全性需求
- 某个报文M的 MAC必须要短小
- 要有 认证性,发送接收双方必须共享 秘密,看了有些博客,好像也叫 初始信任,有了初始信任才能有认证。
- Hash不足以保证安全
- 避免“加密运算”
数字签名
签名提到了MAC报文认证,MAC理论的遗留问题:要求通信双方首先要共享 秘密,也称为初始信任,之后才能有认证,双方共享sk,似乎是个很强的要求,但有了 公钥密码体制(PKC),这个问题可以得到解决。
数字签名是认证的重要工具。
为什么需要数字签名:
前面提到了报文认证是用来保护双方之间的数据交换不被第三方侵扰,但它并不能保证 双方自身的相互欺骗。
实例:
假定A发送一个认证的信息给B,双方之间的争议可能有:
- B伪造一个不同的消息( 因为B也有sk),但声称是从A收到的
- A可以否认发过该消息( 因为A可以说是B自己给自己发的),B无法证明A确实发了该消息
问题的症状在于双方都有 sk,都可以进行发消息和验证消息,问题在于发送和验证职责的分离。
数字签名的直观定义:
目标:防止报文被伪造,用于保证数据的完整性
操作:签名者对报文产生一串 公开且他人无法伪造的数据串,公开是为了给他人验证,无法伪造是保证发送方无法否认发过该消息。
方法:PKC+Hash PKC用私钥加密,公钥解密,提供认证性,Hash提供消息的完整性。
数字签名应具有的性质
- 必须能够验证签名者以及签名的日期,时间等
- 必须能够认证签名的报文内容
- 签名能够由第三方验证,以解决收发双发的争议
认证系统
证书
证书的定义: 公钥 <------> 用户
通俗将:数字证书就是把 公钥与其所有者的身份进行 绑定的文档。
而绑定的方法就是: 权威机构(证书颁布机构)CA的数字签名。
两个实体:
- 证书用户:使用证书的实体
- 证书所有者:证书中的主体,证书中公钥的持有者
证书的格式
-
版本号 Version:区分证书的不同版本
-
证书序列号 Serial number 一个证书,在CA中 唯一标识证书
-
签名算法标识:带参数的,用于给证书签名的算法
-
发行商名字 Issuer name 创建签名证书的签证机构CA的名字
-
有效期 生效日期和终止日期
-
证书主体名 获得证书的用户名,证明拥有相应密钥的主体是公钥的所有者
-
发行商唯一标识
-
证书主体唯一标识
-
… 拓展
-
签名:用CA私钥对证书的 所有域及这些域的Hash的值一起加密( 用私钥)
PKI Public Key Infrastructure 公钥基础设施
用来提供可靠易用的 公钥密码操作的 系统的总称。
主要目标:保障大型开放式网络环境下的网络和信息安全
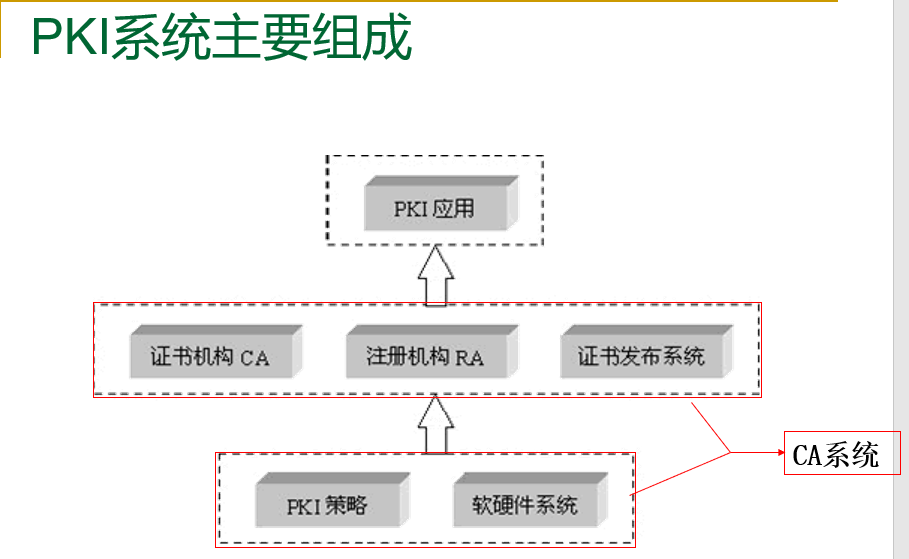
PKI系统的主要组成:

PKI系统主要组成:
- PKI策略 定义和建立了一个组织信息安全方面的指导方针,同时也定义了密码系统使用的处理方法和原则
- 认证机构CA(Certificate Authority)系统
PKI的信任基础,它管理了 公钥的整个生命周期,其作用包括:审计用户身份的RA,发放证书,规定证书的有效期和通过发布证书废除列表确保必要时可以废除证书。 - PKI应用
为各种应用提供访问PKI的方式
认证机构CA系统
PKI的 核心是认证机构CA系统。
CA系统:
- 权威的,可信任的,公正的第三方机构
- 认证中心
- PKI的核心
- 数字证书的 签发机构
- 负责证书的产生,存档,发放,查询,恢复以及作废管理
- 一个典型的CA系统包括安全服务器, 注册机构RA,CA服务器,LDAP目录服务器和数据库服务器等。
注册机构RA:
-
RA是数字证书 注册审批机构
-
RA提供用户和CA之间的一个接口,它获取并认证用户的身份,向CA 提出证书请求,它主要完成 收集用户信息和 确认用户身份的功能
-
它接受用户的注册申请,审查用户的申请资格,并决定是否同意CA给其签发数字证书。
-
注:
注册机构并不给用户签发证书,而只是对用户进行资格审查。
CA的任务:
- 验证并标识证书申请者的身份
- 签发证书
- 证书资料信息的管理( 公钥证书序列号,CA标识)
- 产生和发布撤销证书列表
- 证书的归档
- 密钥归档与恢复
- 历史数据归档
CA的职责:
- 确保CA用于签名证书的非对称密钥的质量
- 确保整个签证过程的安全性, 确保签名私钥的安全性
- 确保证书主体标识的唯一性,防止重名
CA的密钥:
- 是整个证书机制得以运行的基础
- CA私钥由CA保管,必须确保 CA私钥的高度机密性
- CA公钥在网上公开,必须保证 CA公钥的完整性
为什么需要PKI?
身份认证的目的是要确定对方的身份是否是 真实或 合法的,为了达到这一目的,需要建立初始信任(双方已经共享了的 秘密),但在网络环境下,建立初始信任需要建立一条 安全通道,这一任务在公钥密码提出之前是非常困难的,代价也很高。而公钥密码提出后,可以用公钥密码手段( 一个公钥,一个私钥,用公钥传递私钥)传递 秘密,如Diffie-Hellman。但 公钥的真实性又难以保证,如何确定一个人和他所持有的公钥的关系,已经公钥是否在有效期内,签名算法是什么?所以 可信的第三方系统被提了出来,如A与B想建立一条安全路径时,可以寻找共同信任的第三方,在可信第三方的帮助下实现A对B所拥有的 公钥的鉴别,从而建立初始信任。
而PKI就是这样一个 第三方系统,可以让可信第三方( CA)对用户的公钥 签署证书,只要验证证书的合法性,就可以相信 公钥证书中所描述的 关于公钥的信息,如证书主体,有效期等证书域是可信的。
认证协议
实体认证的两种方式
弱认证:基于口令的认证
强认证:质询-应答协议
弱认证
用户提供一个口令,计算机验证该口令,如果输入的口令和该用户相对应的口令( 可能存放在数据库中)对比不一致,则用户的身份得到认证,否则拒绝该口令,认证失败。
口令的脆弱性:
-
字典攻击( 在线,离线):攻击者可以 穷举字典的口令,猜测出特定用户的口令,但需要有两个条件:
- 口令在字典中
- 可以判断选用的口令是否正确
因此要尽量避免 口令泄露
口令又是如何泄露的呢?-
网络明文传输
-
口令文件非法访问
解决的办法:使用一个单向的hash函数将口令hash成 伪随机数。对口令进行散列( 加盐)
-
工作站劫持
-
用户误用
-
搭线窃听
强认证
这部分协议主要就是发送一个数,用 密钥进行验证或解密,我个人还不是很熟悉。
安全策略,访问控制
安全策略
安全策略 为系统定义安全
安全策略将系统状态划分为两类
- 授权状态 Authorized 系统允许进入的状态,安全的
- 非授权状态 Unauthorized 不安全的,如果系统进入这些状态,则违反了安全规定
安全系统
定义一
安全系统是一种 始于已授权状态,但不能进入未授权状态的系统。
定义二
如果系统进入了一个未授权状态,则称发生了一次安全破坏
定义三
保密性:设X是实体的集合,并设I是信息,如果X中成员不能获取信息I,那么I关于X具有 保密性。
定义四
完整性:设X是实体的集合,并设I是某些信息或某种资源,如果X中所有成员都信任I,那么I关于X具有 完整性。
定义五
可用性:设X是实体的集合,并设I是一种资源,如果X中所有的成员都可以访问I,那么I关于X是具有 可用性的。
以上 保密性, 完整性, 可用性的定义都用到了集合的方法来表达,小结
- 不可获取信息(保密)
- 信任(完整性)
- 访问的服务质量(可用性)
与ISO的CIA定义的区别是: 此处没有攻击者
定义六
安全机制是实施安全策略的某些部分的实体或规程。
定义七
安全模型是表达特定策略或策略集合的模型。
两个结论
- 计算机系统的安全性是不可判定问题
- 判断一个程序是否为病毒是不可判定问题
访问控制
"防止未经授权使用资源,包括防止以非授权方式使用资源",是计算机安全的 核心元素
访问控制策略
-
自主访问控制 DAC
- 基于请求者的身份和访问规则
- 实体可授权
-
强制访问控制 MAC
-
基于安全许可( 实体的能力)和安全标记( 资源的敏感度)
-
实体不可对另一实体授权
-
-
基于角色的访问控制 RBAC
访问控制的基本元素
- 主体 - entity that can access objects
- 进程
- 三类:owner,group,world
- 客体 access controlled resource
- 资源
- 访问权 way in which subject accessed an object
- e.g read,write,execute,delete,create
自主访问控制
- 访问控制矩阵
- 主体: 行
- 客体: 列
- 矩阵元素: 权限(访问权)
但在一个系统中,访问控制矩阵会显得很大,因为其中有许多的矩阵元素是0(也就是主体和客体毫无关系的),改进思路: 稀疏矩阵, 可分解
访问控制列表ACL
- 概念上,ACL就像访问控制矩阵的列。
- 针对每一个客体,列出 用户和权限
- 特点:简化,高效
能力表:又称能力权证,C-List
- 概念上能力表就像访问控制矩阵的行。
- 针对用户,指示用户所能访问的 客体及其权限
ACL与C-List比较
给定主题,确定它能访问哪些客体,访问的权限是?
- 使用能力表更简单
给定客体,确定有哪些主体能够访问,访问的权限是?
- 使用访问控制表回答简单
强制性访问控制
- 基于安全许可( 实体的能力)和安全标记( 资源的敏感度)
- 实体不可对另一实体授权
BLP模型
按线性排列定义 安全许可(clearance),对应于军事安全中的安全许可
- Top Secret (TS):最高
- Secret (S)
- Confidential ©
- Unclassified (UC):最低
主体有安全许可,客体有安全密级,有时候统称为 安全密级
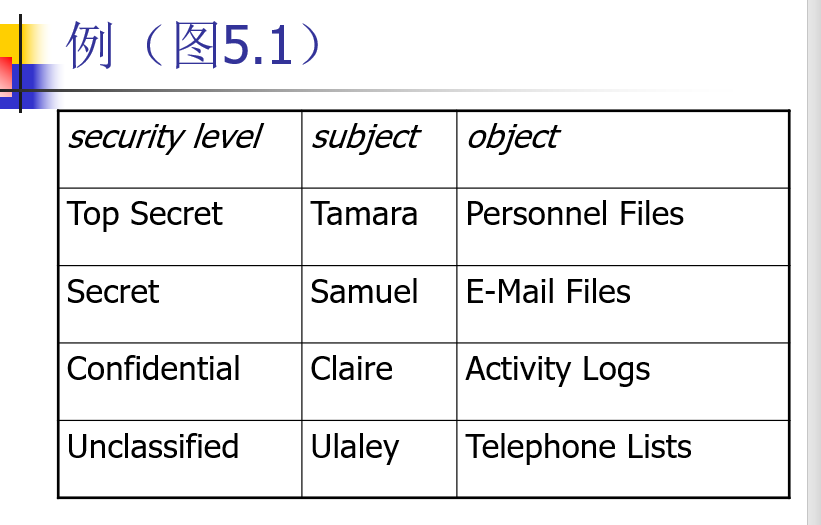
BLP模型:
-
防止主体读取安全密级比它的安全许可更高的客体。
-
简单安全条件,预备版本:S可以读O,当且仅当lo<=ls,且S对O具有自主性读权限 -
具有自主型读权限,意味着与自主访问控制部分相对应的S和O的访问控制矩阵条目中包含 一项读的权限。
-
*-属性( 星号属性),预备版本:S可以写O,当且仅当ls<=lo,且S对O具有自主型写权限。
-
基本安全定理,预备版本:设系统的的某一个 初始安全状态为σ0\sigma_{0}σ0,T是状态转换的集合。如果T的每个元素都遵守 简单安全条件(预备版)和*-属性(预备版),那么对于每个i>=0,状态σi\sigma_{i}σi都是安全的。
小结Bell-LaPadula模型:
- 简单安全条件: 不向上读(no reads up)
- *-属性: 不向下写(no writes down)
- 基本安全定理,如果初始状态为安全的系统,且所有状态转换都满足简单安全条件和星号属性,则系统中的所有状态都是安全的。
- 本质是 强制型访问控制,但结合了自主型访问控制的内容。
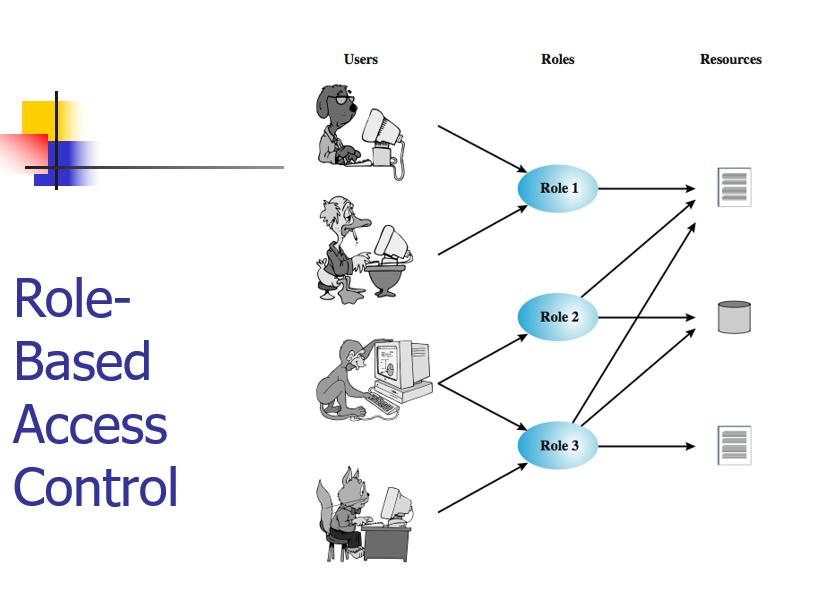
基于角色的访问控制
- 基于角色而非身份的控制
- 基于角色授权,而不是单独给用户授权
参考资料:
-
bintou老师课件
-
《密码与编码学与网络安全》第七版