If you have some education in Machine Learning, the name Nearest Neighbor probably reminds you of the k-nearest neighborsalgorithm. It is a very simple algorithm with seemingly no “learning” actually involved: The kNN rule simply classifies each unlabeled example by the majority label among its k-nearest neighbors in the training set.
This seems like a very naive, even “silly”, classification rule. Is it? Well, depends on what you take as your distance metric, i.e: how do you choose to measure the similarity between examples. Yes, the naive choice — using simple Euclidean distance in the “raw” features — often usually leads to very poor results in practical applications. For example, here are two examples (images) whose pixel-values are close in Euclidean distance; but arguably, one would be crazy to classify the left image as a flower, solely based on it being a neighbor of the right image.
But, as it turns out, coupling the kNN rule with the proper choice of a distance metric can actually be extremely powerful. The field of “metric learning” demonstrated that when machine learning is applied to learning the metric prior to using the kNN rule, results can improve significantly.
The great thing about our current “Deep Learning era” is the abundance of available pre-trained networks. These networks solve certain classification tasks (predicting an image category, or the text surrounding a word), but the interesting thing is not so much their success on those tasks, but actually the extremely useful by-product they provide us with: dense vector representations, for which simple Euclidean distance actually corresponds to high-level, “semantic” similarity.
The point is that for many tasks (but namely, general-purpose images and text), we already have a good distance metric, so now we actually can just use the simple kNN rule. I’ve talked about this point a lot in the past — e.g, in a previous post I attempted to use such searches to verify the claim that generative models are really learning the underlying distributionand not just memorizing examples from the training set.
This leaves us with the task of actually findingthe nearest neighbors (I will refer to this as a NN query). This problem — now a building block in literally anyML pipeline — has received a lot of traction, both in the CS-theory literature and from companies that need highly optimized solutions for production environments. Here again, the community benefits, because a couple of the big players in this field have actually open-sourced their solutions. These tools use carefully crafted data structures and optimized computation (e.g on GPUs) to efficiently implement NN queries. Two of my favorites are Facbook’s FAISSand Spotify’s Annoy. This post should hopefully bring you up to speed on what happens “behind the hood” of these libraries.
A first distinction when we talk about nearest neighbors queries is between exactand approximatesolutions.
Exact algorithmsneed to return the k nearest neighbors of a given query point in a dataset. Here, the naive solution is to simply compare the query element to each element in the dataset, and choose the k that had the shortest distances. This algorithm takes O(dN), where N is the size of the dataset and d is the dimensionality of the instances. At first glance this might actually seem satisfactory, but think about it: 1) this is only for a single query! 2) while true that d is fixed, it can often be very large, and most importantly 3) in the “big data” paradigm, when datasets can be huge, being linear in the dataset size is no longer satisfactory (even if you’re Google or Facebook!). Other approaches for exact queries use tree structures and can achieve better average complexity but their worst-case complexity still approaches something that’s linear in N.
Approximate algorithmsare given some leeway. There are a couple of different formulations, but the main idea is that they only need to return instances whose distance to the query point is almostthat of the real nearest neighbors (where ‘almost’ is the algorithm’s approximation factor). Allowing for approximate solutions opens the door to randomized algorithms, that can perform an ANN (approximate NN) query in sublineartime.
Part 3: Locality Sensitive Hashing
Generally-speaking, a common and basic building block for implementing sublinear time algorithms are hash functions. A hash function is any function that maps input into data of fixed size (usually of lower dimension). The most famous example, which you might have encountered by simply downloading files off the internet, is that of checksumhashes. The idea behind them is to generate a “finger-print” — i.e, some number that is hopefully unique for a particular chunk of data — that can be used to verify that the data was not corrupted or tampered with when it was transferred from one place to another.
These hash functions were designed with this sole purpose in mind. This means that they are actually very sensitive to small changes in the input data; even a single bit that’s changed will completely change the hash value. While this is really what we need for exact duplicate detection(e.g, flagging when two files are really the same), it’s actually the opposite of what we need for near duplicatedetection.
This is precisely what Locality Sensitive Hashing (LSH) attempts to address. As it’s name suggest, LSH depends on the spatiality of the data; in particular, data items that are similar in high-dimension will have a larger chance of receiving the same hash value. This is the goal; there are numerous algorithms that construct hash functions with this property. I will describe one approach, that is amazingly simple and demonstrates the incredibly surprising power of random projections (for another example, see the beautiful Johnson-Lindenstrauss lemma).
The basic idea is that we generate a hash (or signature) of size k using the following procedure: we generate k random hyperplanes; the i-th coordinate of the hash value for an item x is binary: it is equal to 1 if and only if x is above the i-th hyperplane.
The entire algorithms is just repeating this procedure L times:
Let’s understand how LSH can be used to perform ANN queries. The intuition is as follows: If similar items have (with high probability) similar hashes, then given a query item, we can replace the “naive” comparison against all the items in the dataset, with a comparison only against items with similar hashes(in the common jargon, we refer to this as items that landed “in the same bucket”). Here we see that the fact that we were willing to settle for accuracy is precisely what allows for sublinear time.
Since inside the bucket we compute exact comparisons, the FP probability (i.e, saying that an item is a NN when it truly isn’t) is zero, so the algorithm always has perfect precision; however, we will only return items from that bucket, so if the true NN was not originally hashed to the bucket, we have no way of returning it. This means that in the context of LSH, when we talk about accuracy we really mean recall.
Formally, an ANN query using LSH is performed as follows: 1) Find the “bucket” (hash value) of the query item 2) Compare against every other item in the bucket.
Let’s analyze the computational complexity of this algorithm. It will be quick and easy, I promise!
Stage 1) costs dk; Stage 2) costs N/2^kin expectation (because there are N points in the dataset and 2^K regions in our partitioned space). Since the entire procedure is repeated L times, the total cost is, on average, LDK+LDN/2^k. When k and L are taken to be about logN, we get the desired O(logN).
Part 4: LSH Hyperparameters, or the accuracy-time tradeoff
We’ve seen the basic algorithm for LSH. It has two parameters, k (size of each hash) and L (the number of hash-tables) — different setting of the values for k,L correspond to different LSH configurations, each with its own time complexity and accuracy.
Analyzing these formally is a little tricky and requires much more math, but the general take-away is this:
By careful setting of these parameters, you can get a system that is arbitrarily accurate (what-ever you definition of a “near duplicate” is), BUT some of these can come at a cost of a very large L , i.e a large computational cost.
Generally a good approach for settling such trade-offs empiricallyis to quantify them on a well-defined task, which you can hopefully design using minimal manual labor. In this case, I used the Caltech101dataset (yes, it’s old; yes, there were image datasets that predated ImageNet!), with images of 101 simple objects. As input to my LSH scheme, I used the 4096-dimensional feature-vectors obtained by passing each image through a pre-trained VGG network. To keep things simple, I assumed that the other images from the same category are true NN in the feature space.
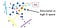
With a “ground truth” at hand, we can try out different hyperparameter combinations and measure their accuracy (recall) and runnning time. Plotting the results gives a nice feel for the accuracy-time trade-off:
We clearly see that better recall comes at the cost of longer run-time. Note that the actual results are task-dependent: generally speaking, the more similar (in high-dimension) the items you consider “near” are, the easier the task will be. Finding distantneighbors efficientlyis a hard task, beware!
Part 5: Putting it all together for an example application
I wanted to piece together this pipeline for a personal project, which is to more efficiently browse my personal photo collection. Returning from a trip, I often have photos from several devices, and many of them are so similar — my appreciation for the views usually leaves me with tens of photos of pretty much the same things. Semantic similarity to the rescue! Here are some of the results.
Each row represents a single query; on the left is the query image, and on the right are the images that were hashed to the same bucket, with their actual distance in green. Pretty cool stuff!
Summary (TL;DR).
We reviewed two really useful ideas:
Finally, we saw how the combination of these two ideas — namely, applying LSH not on the raw data (image, text) but on the deep representation — can be used to perform fast similarity search in huge collections.