[原]异常检测--综述

标签： | 发表时间：2018-12-04 20:00 | 作者：App_12062011
出处：https://blog.csdn.net/App_12062011

异常点检测，有时也叫离群点检测，英文一般叫做Novelty Detection或者Outlier Detection，这里就对异常点检测算法做一个总结。

1. 异常点检测算法使用场景

　　　　什么时候我们需要异常点检测算法呢？常见的有三种情况。一是在做特征工程的时候需要对异常的数据做过滤，防止对归一化等处理的结果产生影响。二是对没有标记输出的特征数据做筛选，找出异常的数据。三是对有标记输出的特征数据做二分类时，由于某些类别的训练样本非常少，类别严重不平衡，此时也可以考虑用非监督的异常点检测算法来做。

              具体应用场景有，欺诈检测，入侵检测，生态系统失调，公共卫生，医疗等。

2. 异常点检测算法常见类别

　　　　异常点检测的目的是找出数据集中和大多数数据不同的数据，常用的异常点检测算法一般分为三类。

　　　　第一类是基于统计学的方法来处理异常数据，这种方法一般会构建一个概率分布模型，并计算对象符合该模型的概率，把具有低概率的对象视为异常点。比如特征工程中的 RobustScaler方法，在做数据特征值缩放的时候，它会利用数据特征的分位数分布，将数据根据分位数划分为多段，只取中间段来做缩放，比如只取25%分位数到75%分位数的数据做缩放。这样减小了异常数据的影响。

　　　　第二类是基于聚类的方法来做异常点检测。这个很好理解，由于大部分聚类算法是基于数据特征的分布来做的，通常如果我们聚类后发现某些聚类簇的数据样本量比其他簇少很多，而且这个簇里数据的特征均值分布之类的值和其他簇也差异很大，这些簇里的样本点大部分时候都是异常点。比如 BIRCH聚类算法原理和 DBSCAN密度聚类算法都可以在聚类的同时做异常点的检测。

　　　　第三类是基于专门的异常点检测算法来做。这些算法不像聚类算法，检测异常点只是一个赠品，它们的目的就是专门检测异常点的，这类算法的代表是One Class SVM和Isolation Forest.

3.基于统计学的异常检测

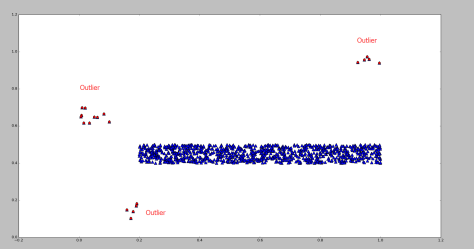
异常点（outlier）是一个数据对象，它明显不同于其他的数据对象，就好像它是被不同的机制产生的一样。例如下图红色的点，就明显区别于蓝色的点。相对于蓝色的点而言，红色的点就是异常点。

outlier

 

（一）基于正态分布的一元离群点检测方法

假设有 n 个点  (x_{1},...,x_{n})，那么可以计算出这 n 个点的均值 \mu 和方差 \sigma。均值和方差分别被定义为：

\mu=\sum_{i=1}^{n}x_{i}/n,

\sigma^{2}=\sum_{i=1}^{n}(x_{i}-\mu)^{2}/n.

在正态分布的假设下，区域  \mu\pm 3\sigma 包含了99.7% 的数据，如果某个值距离分布的均值 \mu 超过了 3\sigma，那么这个值就可以被简单的标记为一个异常点（outlier）。

（二）多元离群点的检测方法

涉及两个或者两个以上变量的数据称为多元数据，很多一元离群点的检测方法都可以扩展到高维空间中，从而处理多元数据。

（1）基于一元正态分布的离群点检测方法

假设 n 维的数据集合形如  \vec{x}_{i}=(x_{i,1},...,x_{i,n}), i\in \{1,...,m\}，那么可以计算每个维度的均值和方差 \mu_{j},\sigma_{j}, j\in\{1,...,n\}. 具体来说，对于 j\in \{1,...,n\}，可以计算

\mu_{j}=\sum_{i=1}^{m}x_{i,j}/m

\sigma_{j}^{2}=\sum_{i=1}^{m}(x_{i,j}-\mu_{j})^{2}/m

在正态分布的假设下，如果有一个新的数据  \vec{x}，可以计算概率 p(\vec{x}) 如下：

p(\vec{x})=\prod_{j=1}^{n} p(x_{j};\mu_{j},\sigma_{j}^{2})=\prod_{j=1}^{n}\frac{1}{\sqrt{2\pi}\sigma_{j}}\exp(-\frac{(x_{j}-\mu_{j})^{2}}{2\sigma_{j}^{2}})

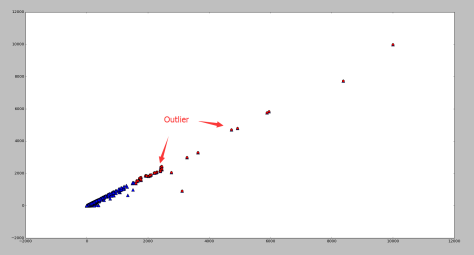
根据概率值的大小就可以判断 x 是否属于异常值。运用该方法检测到的异常点如图，红色标记为异常点，蓝色表示原始的数据点。

Gauss

（2）多元高斯分布的异常点检测

假设 n 维的数据集合  \vec{x}=(x_{1},...,x_{n}),，可以计算 n 维的均值向量

\vec{\mu}=(E(x_{1}),...,E(x_{n}))

和  n\times n 的协方差矩阵：

\Sigma=[Cov(x_{i},x_{j})], i,j \in \{1,...,n\}

如果有一个新的数据  \vec{x}，可以计算

p(\vec{x})=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}} \exp(-\frac{1}{2}(\vec{x}-\vec{\mu})^{T}\Sigma^{-1}(\vec{x}-\vec{\mu}))

根据概率值的大小就可以判断  \vec{x} 是否属于异常值。

（3）使用 Mahalanobis 距离检测多元离群点

对于一个多维的数据集合 D，假设  \overline{a} 是均值向量，那么对于数据集 D 中的其他对象 a，从 a 到 \overline{a} 的 Mahalanobis 距离是

MDist(a,\overline{a})=\sqrt{(a-\overline{a})^{T}S^{-1}(a-\overline{a})},

其中  S 是协方差矩阵。

在这里， MDist(a,\overline{a}) 是数值，可以对这个数值进行排序，如果数值过大，那么就可以认为点 a 是离群点。或者对一元实数集合 \{MDist(a,\overline{a})|a\in D\} 进行离群点检测，如果 MDist(a,\overline{a}) 被检测为异常点，那么就认为 a 在多维的数据集合 D 中就是离群点。

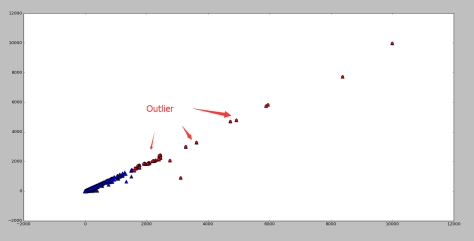
运用 Mahalanobis 距离方法检测到的异常点如图，红色标记为异常点，蓝色表示原始的数据点。

Mahalanobis

（4）使用  \chi^{2} 统计量检测多元离群点

在正态分布的假设下， \chi^{2} 统计量可以用来检测多元离群点。对于某个对象 \bold{a}， \chi^{2} 统计量是

\chi^{2}=\sum_{i=1}^{n}(a_{i}-E_{i})^{2}/E_{i}.

其中， a_{i} 是 \bold{a} 在第 i 维上的取值， E_{i} 是所有对象在第 i 维的均值，n 是维度。如果对象  \bold{a} 的 \chi^{2} 统计量很大，那么该对象就可以认为是离群点。

运用  \chi^{2} 统计量检测到的异常点如图，红色标记为异常点，蓝色表示原始的数据点。

ChiSquare

4.基于矩阵分解的异常检测

在介绍这种方法之前，先回顾一下主成分分析（Principle Component Analysis）这一基本的降维方法。

（一）主成分分析（Principle Component Analysis）

对高维数据集合的简化有各种各样的原因，例如：

（1）使得数据集合更容易使用；

（2）降低很多算法的计算开销；

（3）去除噪声；

（4）更加容易的描述结果。

在主成分分析（PCA）这种降维方法中，数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据集本身所决定的。第一个新坐标轴的方向选择的是原始数据集中方差最大的方向，第二个新坐标轴的选择是和第一个坐标轴正交并且具有最大方差的方向。该过程一直重复，重复的次数就是原始数据中特征的数目。如此操作下去，将会发现，大部分方差都包含在最前面的几个新坐标轴之中。因此，我们可以忽略余下的坐标轴，也就是对数据进行了降维的处理。

为了提取到第一个主成分（数据差异性最大）的方向，进而提取到第二个主成分（数据差异性次大）的方向，并且该方向需要和第一个主成分方向正交，那么我们就需要对数据集的协方差矩阵进行特征值的分析，从而获得这些主成分的方向。一旦我们计算出了协方差矩阵的特征向量，我们就可以保留最大的 N 个值。正是这 N 个值反映了 N 个最重要特征的真实信息，可以把原始数据集合映射到 N 维的低维空间。

提取 N 个主成分的伪代码如下：

去除平均值

计算协方差矩阵

计算协方差矩阵的特征值和特征向量

将特征值从大到小排序

保留最大的N个特征值以及它们的特征向量

将数据映射到上述N个特征向量构造的新空间中

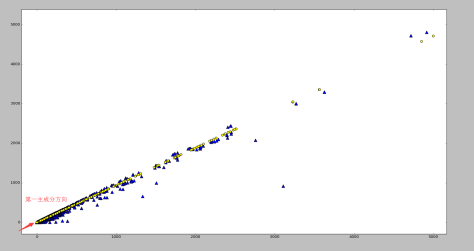
通过 Python 的 numpy 库和 matplotlib 库可以计算出某个二维数据集合的第一主成分如下：原始数据集使用蓝色的三角形表示，第一主成分使用黄色的圆点表示。

PCA

Principle Component Analysis 的基本性质：

Principle component analysis provides a set of eigenvectors satisfying the following properties:

（1）If the top-k eigenvectors are picked (by largest eigenvalue), then the k-dimensional hyperplane defined by these eigenvectors, and passing through the mean of the data, is a plane for which the mean square distance of all data points to it is as small as possible among all hyperplanes of dimensionality k.

（2）If the data is transformed to the axis-system corresponding to the orthogonal eigenvectors, the variance of the transformed data along each eigenvector dimension is equal to the corresponding eigenvalue. The covariances of the transformed data in this new representation are 0.

（3）Since the variances of the transformed data along the eigenvectors with small eigenvalues are low, significant deviations of the transformed data from the mean values along these directions may representoutliers.

（二）基于矩阵分解的异常点检测方法

基于矩阵分解的异常点检测方法的关键思想是利用主成分分析去寻找那些违背了数据之间相关性的异常点。为了发现这些异常点，基于主成分分析（PCA）的算法会把原始数据从原始的空间投影到主成分空间，然后再把投影拉回到原始的空间。如果只使用第一主成分来进行投影和重构，对于大多数的数据而言，重构之后的误差是小的；但是对于异常点而言，重构之后的误差依然相对大。这是因为第一主成分反映了正常值的方差，最后一个主成分反映了异常点的方差。

假设 dataMat 是一个 p 维的数据集合，有 N 个样本，它的协方差矩阵是 X。那么协方差矩阵就通过奇异值分解写成：

X=PDP^{T},

其中 P 是一个 (p,p) 维的正交矩阵，它的每一列都是 X 的特征向量。D 是一个 (p,p) 维的对角矩阵，包含了特征值  \lambda_{1},...,\lambda_{p}。从图像上看，一个特征向量可以看成 2 维平面上面的一条线，或者高维空间里面的一个超平面。特征向量所对应的特征值反映了这批数据在这个方向上的拉伸程度。通常情况下，可以把对角矩阵 D 中的特征值进行从大到小的排序，矩阵 P 的每一列也进行相应的调整，保证 P 的第 i 列对应的是 D 的第 i 个对角值。

这个数据集 dataMat 在主成分空间的投影可以写成

Y=dataMat\times P.

需要注意的是做投影可以只在部分的维度上进行，如果使用 top-j 的主成分的话，那么投影之后的数据集是

Y^{j}=dataMat \times P^{j},

其中  P^{j} 是矩阵 P 的前 j 列，也就是说 P^{j} 是一个 (p,j) 维的矩阵， Y^{j} 是一个 (N,j) 维的矩阵。如果考虑拉回映射的话（也就是从主成分空间映射到原始空间），重构之后的数据集合是

R^{j}=(P^{j}\times (Y^{j})^{T})^{T}=Y^{j}\times (P^{j})^{T},

其中  R^{j} 是使用 top-j 的主成分进行重构之后形成的数据集，是一个 (N,p) 维的矩阵。

下面可以定义数据  dataMat_{i}=(dataMat_{i,1},...,dataMat_{i,p}) 的异常值分数（outlier score）如下：

score(dataMat_{i})=\sum_{j=1}^{p}(|dataMat_{i}-R_{i}^{j}|)\times ev(j)

ev(j)=\sum_{k=1}^{j}\lambda_{k}/\sum_{k=1}^{p}\lambda_{k}

注意到  |dataMat_{i}-R_{i}^{j}| 指的是 Euclidean 范数， ev(j) 表示的是 top-j 的主成分在所有主成分中所占的比例，并且特征值是按照从大到小的顺序排列的。因此，ev(j) 是递增的序列，这就表示 j 越高，越多的方差就会被考虑在 ev(j) 中，因为是从 1 到 j 的求和。在这个定义下，偏差最大的第一个主成分获得最小的权重，偏差最小的最后一个主成分获得了最大的权重 1。根据 PCA 的性质，异常点在最后一个主成分上有着较大的偏差，因此可以获得更高的分数。

整个算法的结构如图所示：

PCC

 

（三）效果展示

下面两幅图使用了同一批数据集，分别采用了基于矩阵分解的异常点检测算法和基于高斯分布的概率模型的异常点算法。

PCC2

基于矩阵分解的异常点检测

 

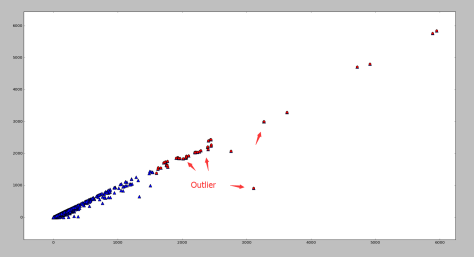
Gauss

基于高斯分布的概率模型的异常点检测

根据图像可以看出，如果使用基于矩阵分解的异常点检测算法的话，偏离第一主成分较多的点都被标记为异常点，其中包括部分左下角的点。需要注意的是如果使用基于高斯分布的概率模型的话，是不太可能标记出左下角的点的，两者形成鲜明对比。

5.基于神经网络Replicator Neural Networks

RNN 算法的主要思想

在这篇文章中，我们将会介绍一个多层的前馈神经网络，该神经网络可以用来进行异常值的检测。这个神经网络模拟的是一个恒等映射，输入层的神经元个数和输出层的神经元个数是一样的。这类的神经网络被称为 Replicator Neural Networks (RNNs)，请注意这里的 RNN 算法指的并不是 Recurrent Neural Networks（RNNs），而是 Replicator Neural Networks，尽管它们拥有着同样的缩写名字 RNNs。具体来说， Replicator Neural Networks (RNNs)，或者说自编码器，是一个多层前馈的神经网络 (multi-layer feed-forward neural networks)。在 Replicator Neural Networks 中，输入的变量也是输出的变量，模型中间层节点的个数少于输入层和输出层节点的个数。这样的话，模型就起到了压缩数据和恢复数据的作用。

rnn1

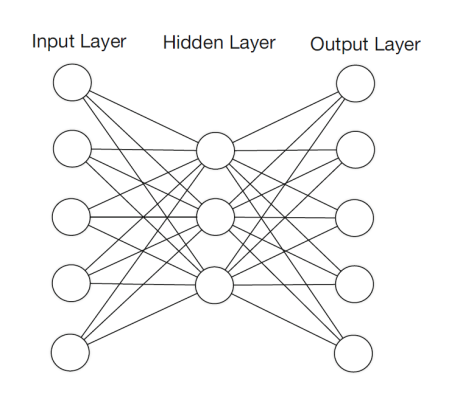
如图所示，这里的 RNNs 有三个隐藏层，输入层和输出层的节点个数都是6，第一个隐藏层和第三个隐藏层的节点个数（图中是4个节点）少于输入层，第二个隐藏层的节点个数是最少的（图中是2个节点）。在神经网络传输的时候，中间使用了 tanh 函数和 sigmoid 函数。这个神经网络是训练一个从输入层到输出层的恒等函数（identity mapping），传输的时候从输入层开始压缩数据，然后到了第二个隐藏层的时候开始解压数据。训练的目标就是使得整体的输出误差足够小，整体的误差是由所有的样本误差之和除以样本的个数得到的。由于图中只画出了6个特征，因此第 i 个样本的误差是

e_{i}=\sum_{j=1}^{6}(x_{i j}-r_{i j})^{2}/6

如果使用已经训练好的 RNN 模型，异常值的分数就可以定义为重构误差（reconstruction error）。

下面简要介绍一下 RNN 模型是如何构建的：

rnn2

根据上图所示，左边的是输入层，右边的输出层。假设第 k 层中第 i 个神经元的输出是  S_{k}(I_{ki})，其中 I_{ki} 表示第 k 层中第 i 个神经元的输入， S_{k} 表示第 k 层使用的激活函数。那么

\theta=I_{ki}=\sum_{j=0}^{L_{k-1}}w_{kij}Z_{(k-1)j}

其中  Z_{kj} 是第 k 层中第 j 个神经元的输出， L_{k} 是第 k 层神经元的个数。对于第二层和第四层而言 (k=2,4)，激活函数选择为

S_{k}(\theta)=tanh(a_{k}\theta)  \text{ for } k=2 \text{ or } 4,

这里的  a_{k} 是一个参数，通常假设为1。对于中间层 (k=3) 而言，激活函数是一个类阶梯 (step-like) 函数。有两个参数 N 和 a_{3}，N 表示阶梯的个数， a_{3} 表示从这一层到下一层的提升率 (transition rate)：

S_{3}(\theta)=\frac{1}{2}+ \frac{1}{4}\sum_{j=1}^{N-1}tanh(a_{3}(\theta-\frac{j}{N})).

在这里可以假设  a_{3}=100， N=4. 那么  S_{3}(\theta) 就如下图所示。

S3

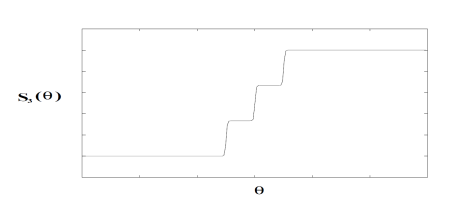
第三层的激活函数的输出就变成了 N 个离散的变量：0, 1/(N-1), 2/(N-1),…,1。这个阶梯型的激活函数是把第三层的连续输入值变成了一批离散的值。也就意味着把样本映射到了 N 个簇，那么 RNN 就可以计算出单个的异常点和一小簇的异常点。

备注：

根据上面的分析，可以看出如果按照以上算法，则不能使用反向传播算法来训练模型，原因是  S_{3}(\theta) 的导数不能够通过它的取值来表示。这一点与 tanh 函数， \sigma 函数是不一致的，因为  tanh^{'}(x) = 1-tanh^{2}(x) 和 \sigma^{'}(x)=\sigma(x)(1-\sigma(x))。因此有学者指出 [1]，使用三个隐藏层是没有必要的，使用1个或者2个隐藏层的神经网络也能够得到类似的结果；同样，没有必要使用 S_{3}(\theta) 这样类型的阶梯函数，使用传统的 \sigma 激活函数也能够得到类似的结果。并且 S_{3}(\theta) 是一个 step-like 函数，很多地方的导数取值都是接近于零的。

后向传播算法：

一般来说，为了训练神经网络模型，需要使用后向传播算法（back propagation），也简称为 BP 算法，或者误差逆传播算法（error back propagation）。在本文中，仅针对最简单的 RNN 模型介绍如何使用 BP 算法进行模型训练，至于多层的神经网络模型或者其他的神经网络模型，方法则是完全类似的。

rnn3

给定训练集合  D=\{(\bold{x}_{1},\bold{y}_{1}),...,(\bold{x}_{m},\bold{y}_{m})\}，其中有 m 个样本，并且输入和输出是一样的值。换句话说，也就是 n 维向量

\bold{x}_{i}=\bold{y}_{i}\in\mathbb{R}^{n} \text{ for all } 1\leq i\leq m.

换句话说，输入样例是由 n 个属性描述，输出的结果也是 n 个属性。隐藏层只有一个，隐藏层的神经元个数是  q=[(n+1)/2]，这里的 [] 表示 Gauss 取整函数。输出层第 j 个神经元的阈值使用 \theta_{j} 表示，隐藏层第 h 个神经元的阈值使用 \gamma_{h} 表示。输入层第 i 个神经元与隐藏层第 h 个神经元之间的连接权重是 v_{i h}, 隐藏层第 h 个神经元与输出层第 j 个神经元之间的连接权重是 w_{h j}, 其中 1\leq i \leq n, 1\leq h \leq q, 1\leq j \leq n.

记隐藏层第 h 个神经元接收到的输入为

\alpha_{h} = \sum_{i=1}^{n}v_{i h}x_{i} \text{ for all } 1\leq h \leq q.

写成矩阵形式就是：

(\alpha_{1},\cdot\cdot\cdot,\alpha_{q})=(x_{1},\cdot\cdot\cdot,x_{n})\begin{bmatrix} v_{11} & ... & v_{1q} \\ ... & ... & ... \\ v_{n1} & ... & v_{nq} \end{bmatrix}.

记输出层第 j 个神经元接收到的输入为

\beta_{j}=\sum_{h=1}^{q}w_{h j}b_{h} \text{ for all } 1\leq j\leq n,

其中  b_{h} 是隐藏层第 h 个神经元的输出， b_{h} = f(\alpha_{h}-\gamma_{h}) \text{ for all } 1\leq h \leq q, f 是激活函数。写成矩阵形式就是：

(\beta_{1},\cdot\cdot\cdot,\beta_{n})=(b_{1},\cdot\cdot\cdot,b_{q})\begin{bmatrix} w_{11} & ... & w_{1n} \\ ... & ... & ... \\ w_{q1} & ... & w_{qn} \end{bmatrix}.

输出层第 j 个神经元的输出是  f(\beta_{j}-\theta_{j}), 其中 1\leq j \leq n.

下面可以假定激活函数都使用  f(x)=1/(1+\exp(-x)), 那么直接通过导数计算可以得到 f^{'}(x)=f(x)(1-f(x)).

对于训练集  (\bold{x}_{k},\bold{y}_{k}), 通过神经网络得到的输出是 \hat{\bold{y}}_{k}=(\hat{y}_{k1},...,\hat{y}_{kn}), 并且  \hat{y}_{kj} = f(\beta_{j}-\theta_{j}) 对于 1\leq j \leq n 都成立。那么神经网络在训练集 (\bold{x}_{k},\bold{y}_{k}) 的均方误差是

E_{k} =\frac{1}{2}\sum_{j=1}^{n}(\hat{y}_{kj}-y_{kj})^{2},

其中  \bold{y}_{k}=(y_{k1},...,y_{kn}). 整体的误差是

E = \frac{1}{m}\sum_{k=1}^{m}E_{k} = \frac{1}{2m}\sum_{k=1}^{m}\sum_{j=1}^{n}(\hat{y}_{kj}-y_{kj})^{2}

标准 BP 算法：

网络中有 个参数需要确定：输入层到隐藏层的 n*q 个权重值，隐藏层到输出层的 n*q 个权重值，q个隐层神经元的阈值，n 个输出层神经元的阈值。BP 算法是一个迭代学习算法，在迭代的每一轮采用了梯度下降法来进行参数的更新。任意参数的更新规则是

v \leftarrow v+ \Delta v.

标准 BP 算法是根据每一个  E_{k} 来获得更新规则，下面来推导每一个参数的更新规则。对于 1\leq h \leq q, 1\leq j \leq n, 计算梯度

\Delta w_{hj} = -\eta \frac{\partial E_{k}}{\partial w_{hj}},

注意到  w_{hj} 先影响到第 j 个输出层神经元的输入值 \beta_{j}, 再影响到第 j 个输出层神经元的输出值 \hat{y}_{kj}，最后影响到 E_{k}，根据高等数学的链式法则可以得到

\frac{\partial E_{k}}{\partial w_{hj}} = \frac{\partial E_{k}}{\partial \hat{y}_{kj}} \cdot \frac{\partial \hat{y}_{kj}}{\partial \beta_{j}} \cdot \frac{\partial \beta_{j}}{\partial w_{hj}}

根据定义  \beta_{j}=\sum_{h=1}^{q}w_{hj}b_{h} 可以得到 \frac{\partial \beta_{j}}{\partial w_{hj}}=b_{h} 对于  1\leq j \leq n 都成立。

根据定义  E_{k}=\frac{1}{2}\sum_{j=1}^{n}(\hat{y}_{kj}-y_{kj})^{2} 可以得到  \frac{\partial E_{k}}{\partial \hat{y}_{kj}}=(\hat{y}_{kj}-y_{kj}).

根据定义  \hat{y}_{kj}=f(\beta_{j}-\theta_{j}) 和 f^{'}(x)=f(x)\cdot(1-f(x)) 可以得到 \frac{\partial \hat{y}_{kj}}{\partial \beta_{j}}=f^{'}(\beta_{j}-\theta_{j})=f(\beta_{j}-\theta_{j})\cdot(1-f(\beta_{j}-\theta_{j}))=\hat{y}_{kj}\cdot (1-\hat{y}_{kj}).

所以可以计算出对于  1\leq h \leq q, 1\leq j \leq n, 有

\frac{\partial E_{k}}{\partial w_{hj}} = (\hat{y}_{kj}-y_{kj})\cdot\hat{y}_{kj}\cdot(1-\hat{y}_{kj})\cdot b_{h}

如果假设

g_{j}=-\frac{\partial E_{k}}{\partial \beta_{j}}=-\frac{\partial E_{k}}{\partial \hat{y}_{kj}}\cdot \frac{\hat{y}_{kj}}{\partial \beta_{j}}

那么可以得到

g_{j}=\hat{y}_{kj}\cdot(1-\hat{y}_{kj})\cdot(y_{kj}-\hat{y}_{kj})

因此对于  1\leq h \leq q, 1\leq j \leq n, 可以得到 \Delta w_{hj}=\eta g_{j}b_{h}.

根据类似的想法，有

\Delta \theta_{j}=-\eta\cdot\frac{\partial E_{k}}{\partial \theta_{j}}, \Delta v_{ih}=-\eta\cdot\frac{\partial E_{k}}{\partial v_{ih}}, \Delta \gamma_{h}=-\eta\cdot\frac{\partial E_{k}}{\partial \gamma_{h}}.

逐个计算：

\frac{\partial E_{k}}{\partial \theta_{j}}=\frac{\partial E_{k}}{\partial \hat{y}_{kj}}\cdot\frac{\partial\hat{y}_{kj}}{\partial\theta_{j}}=(\hat{y}_{kj}-y_{kj})\cdot(-1)\cdot f^{'}(\beta_{j}-\theta_{j})=(y_{kj}-\hat{y}_{kj})\cdot\hat{y}_{kj}\cdot(1-\hat{y}_{kj})=g_{j}

\frac{\partial E_{k}}{\partial v_{ih}}=\frac{\partial E_{k}}{\partial\alpha_{h}}\cdot\frac{\partial\alpha_{h}}{\partial v_{ih}}=\frac{\partial E_{k}}{\partial b_{h}}\cdot\frac{\partial b_{h}}{\partial \alpha_{h}}\cdot\frac{\partial\alpha_{h}}{\partial v_{ih}}

由于

\frac{\partial \alpha_{h}}{\partial v_{ih}}=x_{ki}

\frac{\partial b_{h}}{\partial\alpha_{h}}=f^{'}(\alpha_{h}-\gamma_{h})=f(\alpha_{h}-\gamma_{h})\cdot(1-f(\alpha_{h}-\gamma_{h}))=b_{h}\cdot(1-b_{h})

\frac{\partial E_{k}}{\partial b_{h}}=\sum_{j=1}^{n}\frac{\partial E_{k}}{\partial \beta_{j}}\cdot\frac{\partial \beta_{j}}{\partial b_{h}}=\sum_{j=1}^{n}(-g_{j})\cdot w_{hj}

所以，

\Delta v_{ih}=\eta(\sum_{j=1}^{n}g_{j}w_{hj})\cdot b_{h}\cdot (1-b_{h})x_{ki} = \eta e_{h}x_{ki}, 其中  e_{h}=-\partial E_{k}/\partial\alpha_{h}=(\sum_{j=1}^{n}g_{j}w_{hj})\cdot b_{h}\cdot(1-b_{h}).

\Delta \gamma_{h}=(-\eta)\cdot\frac{\partial E_{k}}{\partial\gamma_{h}}=(-\eta)\cdot\frac{\partial E_{k}}{\partial b_{h}}\cdot\frac{\partial b_{h}}{\partial\gamma_{h}}=\eta\cdot(\sum_{j=1}^{n}g_{j}w_{hj})\cdot(-1)\cdot f^{'}(\alpha_{h}-\gamma_{h})=(-\eta)\cdot(\sum_{j=1}^{n}g_{j}w_{hj})\cdot b_{h}\cdot(1-b_{h})=(-\eta)\cdot e_{h} .

整理之后，任意参数 v 的更新式子是  v\leftarrow v+ \Delta v, 并且更新的规则如下：

\Delta w_{hj}=\eta g_{j}b_{h} \text{ for all } 1\leq j\leq n, 1\leq h \leq q,

\Delta \theta_{j}=-\eta g_{j} \text{ for all } 1\leq j\leq n,

\Delta v_{ih}=\eta e_{h}x_{ki} \text{ for all } 1\leq i\leq n, 1\leq h\leq q,

\Delta \gamma_{h}=-\eta e_{h} \text{ for all } 1\leq h\leq q,

其中学习率  \eta\in(0,1) 控制着算法每一轮迭代中的更新步长，若步长太大则容易振荡，太小则收敛速度过慢，需要人工调整学习率。 对每个训练样例，BP 算法执行下面的步骤：先把输入样例提供给输入层神经元，然后逐层将信号往前传，直到计算出输出层的结果；然后根据输出层的误差，再将误差逆向传播至隐藏层的神经元，根据隐藏层的神经元误差来对连接权和阈值进行迭代（梯度下降法）。该迭代过程循环进行，直到达到某个停止条件为止。

标准 BP 算法的训练流程：
输入：训练集合  D={(\bold{x}_{k},\bold{y}_{k})}_{k=1}^{m} 和学习率  \eta.
过程：
1. 在 (0,1) 范围内随机神经网络中的所有连接权重和阈值
2. repeat
for all  (\bold{x}_{k},\bold{y}_{k}) do
根据当前参数，计算出当前的样本输出  \bold{y}_{k}
计算输出层神经元的梯度项  g_{j}
计算隐藏层神经元的梯度项  e_{h}
更新连接权重  w_{hj}, v_{ih} 与阈值 \theta_{j},\gamma_{h}
end for
3. 达到停止条件
输出：链接权与阈值都确定的神经网络模型

累积 BP 算法：

BP 算法的目的是最小化训练集上的累计误差  E=\sum_{k=1}^{m}E_{k}/m, 其中 m 是训练集合中样本的个数。不过，标准的 BP 算法每次仅针对一个训练样例更新连接权重和阈值，也就是说，标准 BP 算法的更新规则是基于单个的  E_{k} 推导而得到的。通过类似的计算方法可以推导出累计误差的最小化更新规则，那就得到了累计误差逆传播（accumulate error backpropagation）算法。标准 BP 算法需要进行更多次的迭代，并且参数的更新速度快，累积 BP 算法必须扫描一次训练集合才会进行一次参数的更新，而且累计误差下降到一定的程度以后 ，进一步下降就会明显变慢，此时标准 BP 算法往往会更快的得到较好的解，尤其是训练集合大的时候。

训练方法：

（1）把数据集合的每一列都进行归一化；

（2）选择 70% 的数据集合作为训练集合，30% 的数据集合作为验证集合。或者 训练集合 : 验证集合 = 8 : 2，这个需要根据情况而定。

（3）随机生成一个三层的神经网络结构，里面的权重都是随机生成，范围在 [0,1] 内。输入层的数据和输出层的数据保持一致，并且神经网络中间层的节点个数是输入层的一半。

（4）使用后向传播算法（back-propagation）来训练模型。为了防止神经网络的过拟合，通常有两种策略来防止这个问题。（i）第一种策略是“早停”（early stopping）：当训练集合的误差降低，但是验证集合的误差增加时，则停止训练，同时返回具有最小验证集合误差的神经网络；（ii）第二种策略是“正则化”（regularization）：基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分，例如链接权和阀值的平方和。

测试效果：

其中蓝色的点表示正常点，红色的点表示被 RNN 算法标记的异常点。

rnn_result1

rnn_result2

 

作者：App_12062011 发表于 2018/12/04 20:00:04 原文链接 https://blog.csdn.net/App_12062011/article/details/84797641
阅读：0

相关 [异常检测 综述] 推荐：

[原]异常检测--综述

- - 工作笔记
异常点检测，有时也叫离群点检测，英文一般叫做Novelty Detection或者Outlier Detection，这里就对异常点检测算法做一个总结. 1. 异常点检测算法使用场景. 　　　　什么时候我们需要异常点检测算法呢. 一是在做特征工程的时候需要对异常的数据做过滤，防止对归一化等处理的结果产生影响.

异常检测机制

- - 奇虎360-addops
传统的异常检测系统通过设置一个固定的阈值来保证监控项处于正常水平，一旦超过设定的阈值，就会触发报警来提醒人们的注意. 静态阈值法适用于在一定范围内波动的监控项，比如磁盘使用率，CPU使用率等，但是如果遇到网络流量这种不具有明显上限，波动比较剧烈的情况，单纯利用静态阈值法如果设置的阈值比较小，会出现很多误报的情况，增加人工成本；而如果将阈值设置的比较大，又会出现漏报的情况.

异常检测之时间序列的异常检测

- -
其实之前介绍过3倍方差，只是，这里的3倍方差讲的是在时间序列异常检测中的应用. 一个很直接的异常判定思路是，拿最新3个数据点的平均值（tail_avg方法）和整个序列比较，看是否偏离历史总体平均水平太多，如果偏离太多，就报警. 和上述算法基本一致，只是比较对象不是整个序列，而是开始一个小时（其实这种这种思想可以推广，只要是时间序列刚开始的一段时间即可）的以内的数据，求出这段时间的均值和标准差和尾部数据（新产生的数据）用三本方差的方法比较即可.

使用sklearn进行异常检测

- - 标点符
sklearn提供了一些机器学习方法，可用于奇异（Novelty）点或异常（Outlier）点检测，包括OneClassSVM、Isolation Forest、Local Outlier Factor (LOF) 等. 其中OneClassSVM可用于Novelty Detection，而后两者可用于Outlier Detection.

Netflix异常检测工具Surus初探

- - 标点符
Surus是NetFlix开源的UDFs，是基于pig和hive的数据分析工具. Surus中的功能能够解决多种多样的问题，例如评分预测模型、异常检测与模式匹配等. 目前开源的UDF功能主要包括两个，包括ScorePMML和Robust Anomaly Detection (RAD). 预测模型的应用随处可见，然而这些应用都不相同，唯独相同的是模型的创建和部署是相同的.

时间序列异常检测算法梳理

- - 标点符
时间序列的异常检测问题通常表示为相对于某些标准信号或常见信号的离群点. 虽然有很多的异常类型，但是我们只关注业务角度中最重要的类型，比如意外的峰值、下降、趋势变化以及等级转换（level shifts）. 革新性异常：innovational outlier (IO)，造成离群点的干扰不仅作用于$X_T$，而且影响T时刻以后序列的所有观察值.

Libjingle库 综述

- - C++博客_首页
   国内现在很多语音聊天工具都是基于TURN方式实现的，包括YY、AK等等，这种方式对于服务器的性能要求很高，而且在用户量增大的时候，服务器压力也会越来越大，用户的语音质量也会受到很大影响. 而基于P2P方式实现的语聊服务器，就可以极大的避免这种情况的发生，而且用户的语音体验也会非常好.    通过上文( P2P的原理和常见的实现方式(为libjingle开路))我们知道，因为NAT设备没有固定标准的原因，导致并不能100%的实现P2P，但是根据现在通用的ICE&STUN的方式，P2P的成功率可以达到90%多.

RBAC综述(转)

- - 企业架构 - ITeye博客
摘要 基于角色的访问控制（Role-Based Access Control）作为传统访问控制（自主访问，强制访问）的有前景的代替受到广泛的关注. 在RBAC中，权限与角色相关联，用户通过成为适当角色的成员而得到这些角色的权限. 在一个组织中，角色是为了完成各种工作而创造，用户则依据它的责任和资格来被指派相应的角色，用户可以很容易地从一个角色被指派到另一个角色.

如何基于Flink+TensorFlow打造实时智能异常检测平台？只看这一篇就够了

- - zhisheng的博客
本文转自 AI 前线公众号，作者 | 潘国庆 编辑 | Natalie. Flink 已经渐渐成为实时计算引擎的首选之一，从简单的实时 ETL 到复杂的 CEP 场景，Flink 都能够很好地驾驭. 本文整理自携程实时计算负责人潘国庆在 QCon 全球软件开发大会（北京站）2019 的演讲，他介绍了携程如何基于 Flink 与 TensorFlow 构建实时智能异常检测平台，以解决规则告警系统准确率低、时效性低、规则配置复杂与耗费人力等诸多问题，实现了业务指标毫秒级延迟与智能化检测，同时依托 Flink 实现了强大的容错机制.

Big Data技术综述

- Ben - 《程序员》杂志官网
Big Data是近来的一个技术热点，但从名字就能判断它并不是什么新词. 历史上，数据库、数据仓库、数据集市等信息管理领域的技术，很大程度上也是为了解决大规模数据的问题. 被誉为数据仓库之父的Bill Inmon早在20世纪90年代就经常将Big Data挂在嘴边了. 然而，Big Data作为一个专有名词成为热点，主要应归功于近年来互联网、云计算、移动和物联网的迅猛发展.