愤怒的小鸟之死理性派玩法
- 请叫我火矞弟 - 果壳网 guokr.com - 果壳网本文编译自 Rhett Allain 的 Physics of the Yellow Angry Bird. 原文 2011 年 11 月 10 日在《连线》杂志网站上发布. 今天的主角是“愤怒的小鸟”中那只黄色的小鸟（这是早期版本就出现的小鸟之一）. 发射黄鸟之后只要点下屏幕，它就会极速俯冲，击碎障碍物，尤其适合用来对付木桩.
愤怒的小鸟之死理性派玩法
标签：
愤怒
理性
| 发表时间：2011-11-14 22:10 | 作者：莱尼 请叫我火矞弟
出处：http://www.guokr.com/
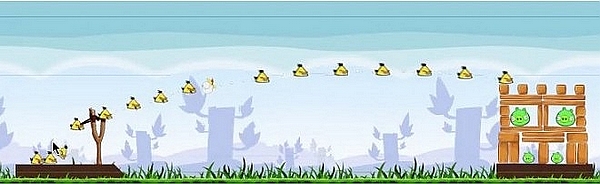
本文编译自 Rhett Allain 的 Physics of the Yellow Angry Bird. 原文 2011 年 11 月 10 日在《连线》杂志网站上发布。
————————————————————————————————————————
今天的主角是“愤怒的小鸟”中那只黄色的小鸟（这是早期版本就出现的小鸟之一）。发射黄鸟之后只要点下屏幕，它就会极速俯冲，击碎障碍物，尤其适合用来对付木桩。要分析黄鸟，可以用 Tracker Video Analysis （一款免费的视频分析和建模软件） 获取“愤怒的小鸟”中黄鸟的飞行数据。现在，我们能直接在 Google Chrome 里面玩儿这款游戏，收集数据只需截屏后用 Tracker Video Analysis 分析就可以了。
要注意的是，游戏里黄鸟真实大小和在屏幕显示的大小有个比例的换算。分析可知，这个游戏中，弹弓的高度大约是 4.9 米。（关于比例尺的详细计算过程，作者 Rhett Allain 在另一篇文章里做了论述， 具体可以看 apple4us 网站上对这篇文章的翻译 Angry Birds 物理学 。）
速度疑云
- 点击过程中的加速情况
点击屏幕前，黄鸟已经有了一定的速度，而点击后速度显然发生了变化。也许点击过程中黄鸟经历了匀加速？下图是 Tracker Video Analysis 生成的图表，显示点击前后小鸟在水平方向（x）和竖直方向（y）分速度的数值变化▼：
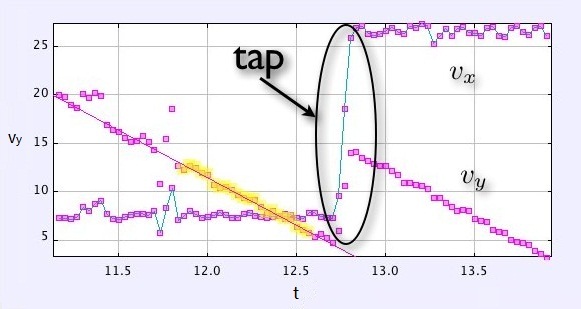
作为验证，我在中比较了点击前小鸟的速度以及点击过程中的加速度（见下图▼）。似乎每次加速都持续了 0.067 秒，当然这很可能跟截屏速度有关。
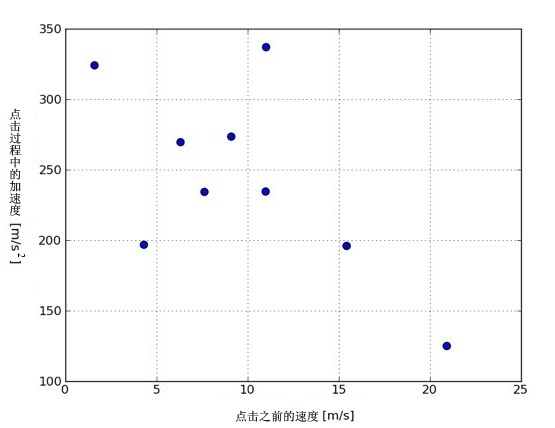
由此可见，完全没有迹象表明点击前小鸟的速度和点击中的加速度之间有简单的关系，加速度也显然不是恒定的，数值上从 124 m/s2 直到 336 m/s2 都有出现。
- 速度的变化
如果比较点击前后瞬间速度的大小呢？虽然前面已经证明了加速度与初速度之间似乎没有关系，但这里还是再来看一下▼：
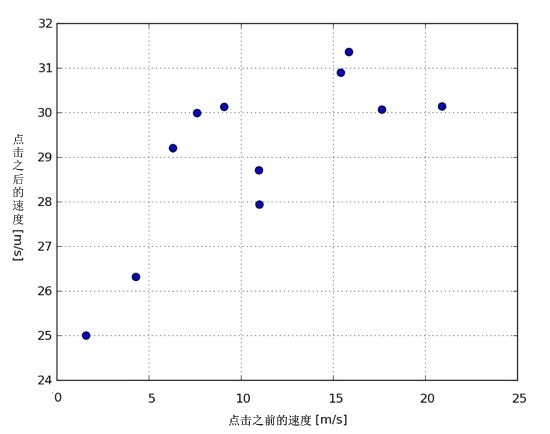
你可能会觉得加速度与初速度之间存在某种关系，但我认为点击之后，黄鸟的速度始终为 30 m/s。不错，的确有一个点在 25 m/s 左右，还有一个在 26 m/s 附近，但绝大多数值都很接近 30 m/s。注意，纵轴不是从 0 开始，而是从 24 m/s 处开始的，这样会使细微的差距会被放大。
下面再来看看末速度的分布图▼：
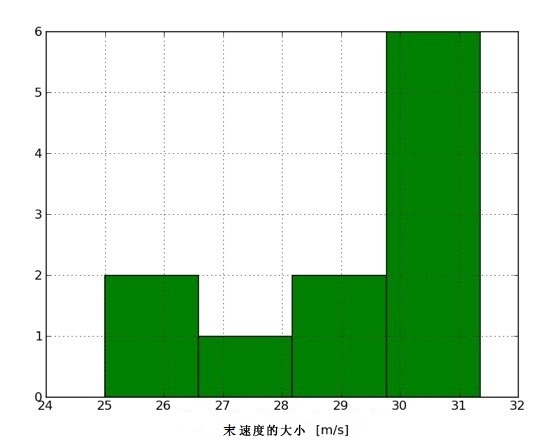
可见，末速度的平均值为 （29.06 ± 1.86）m/s。确实，判断末速度值是否恒定还需要更多的数据。不过，先来看看在点击之前，小鸟在竖直方向上加速度的变化▼。这个值应该在 9.8 m/s2 左右：
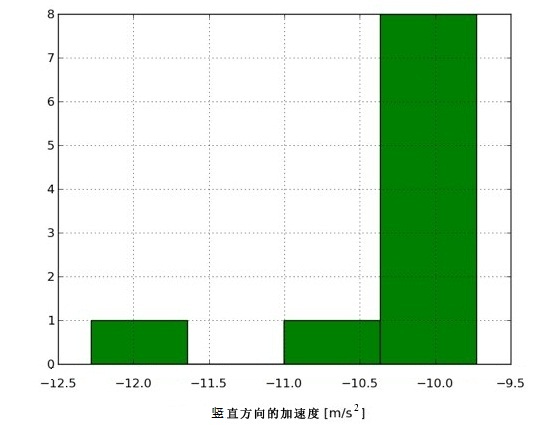
竖直方向的加速度平均值为 （-10.23 ± 0.73）m/s2 。两个分布的标准差与平均值之比很接近，看来，即使是我们确定是恒定的量，在测量中也不一定会有一个恒定的结果。一部分原因在于点击后的运动过程通常太短，很难得到精确的末速度值。
我又做了 5 次黄鸟发射实验，只收集末速度数据。发射时我选择了专门的方位，来确保点击后能有足够长的运动轨迹。下面是所有实验结果绘成的末速度柱状图▼：
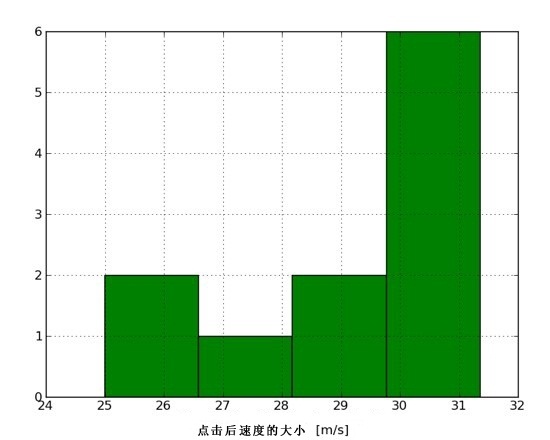
我认为末速度就是 30 m/s，这个数字挺好。真的，你也可以自己试下，把黄鸟竖直向上发射，等它速度接近 0 时点一下——之后的速度会与正常情况中相差无几。
角度疑云
再来看看角度。点击后，黄鸟的速度大小是 30 m/s，角度又如何呢？下面是小鸟运动角度的前后对比图（以地平线为标准）▼，看起来没有任何变化。（真是太好了~）
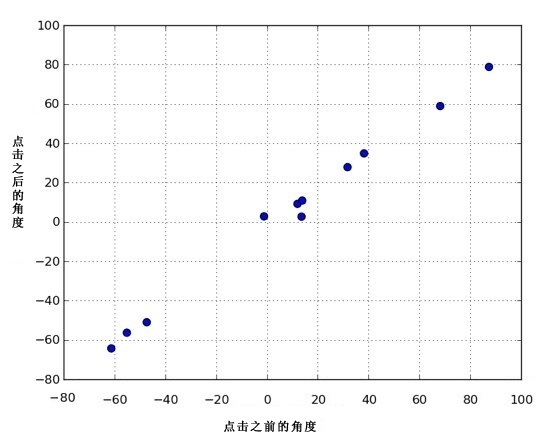
奇怪的加速度乱入
再来看看这张图▼，小鸟在点击后向上飞了，图中显示了黄鸟在水平和竖直方向的运动状况。注意竖直方向上，点击前后都像是抛物线，因为竖直方向上加速度是恒定的。
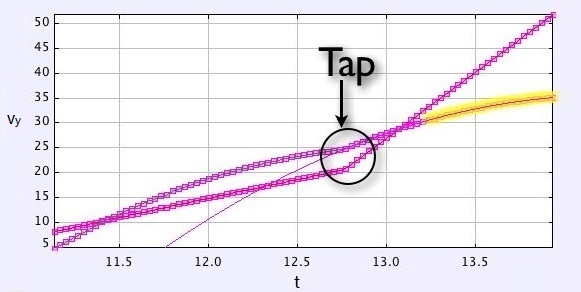
接下来再来看看小鸟向下俯冲时的情况。下图显示了竖直方向上的位移和速度▼。无论分析紫色的、近乎直线的位移图线还是蓝色的速度图线，都可以看出点击后加速度发生了变化。
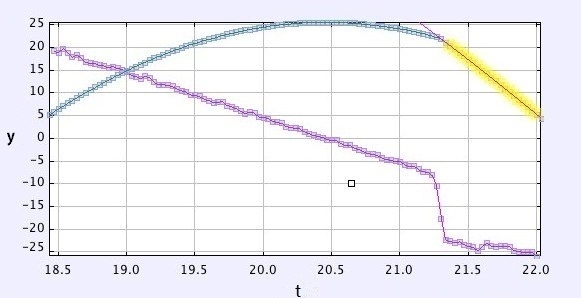
其他情况又如何呢？下图是众多小鸟发射实验所得出的点击后竖直加速度分布▼：
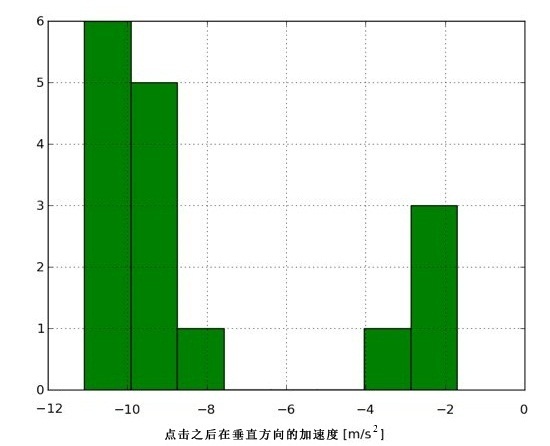
值得注意的是，似乎存在两种不同的加速度。随便玩几次就会发现，如果在黄鸟下降时点击屏幕，加速度会小很多。再上一张竖直加速度与末速度角度的对比图▼：
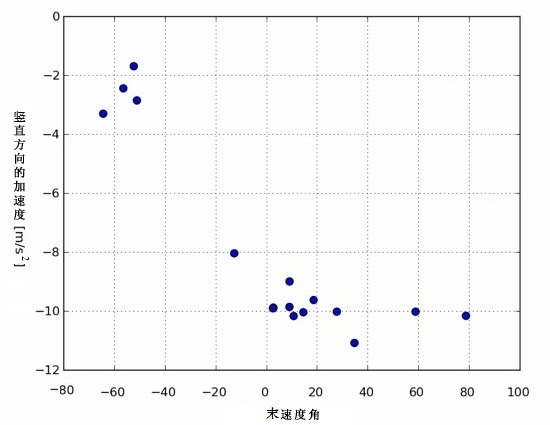
当发射角度小于 -20° 时，竖直加速度的大小为（ -9.8 - -3 ）m/s2 ，也可能加速度为 0，很难分辨。收集更多数据后，我发现加速度的转变看起来没那么急剧。背后也许存在某个函数，留待进一步研究。
综上，我们发现，黄鸟在飞行过程中被加速后，会获得大约 30m/s 的速度，而加速后飞行的方向基本上没有变化。至于点击屏幕那一瞬间加速过程中，其加速度的转变则并没有我们预想中的那么激烈。不过最后要说的是，实践才是最有用的，想玩好愤怒的小鸟，还是多练练才最管用。
相关 [愤怒 理性] 推荐：
2011：愤怒之年？
- coofucoo - FT中文网_英国《金融时报》(Financial Times)存不存在“全球心态”这样一种东西. 我想不出还有什么其它时期，在全球范围内有如此众多的国家被某种形式的街头抗议或民众起义所困扰. 年初的“阿拉伯之春(Arab spring)”为全年定下了基调：在突尼斯和埃及政权垮台后，如今，利比亚的穆阿迈尔•卡扎菲(Muammer Gaddafi)被赶下了台，而叙利亚也爆发了动乱.
理解愤怒情绪并消灭它！
- 小D - 译言-每日精品译文推荐来源Understand Anger and Become Free of It!. It’s important to me; I want to hear about it." An unconscious emotion it may be, an inactive one, it is not!.
愤怒小鸟登陆Chrome Web Store
- Wuvist - Solidotosmsg开源资讯 写道 "wowubuntu消息，在昨天召开的Google I/O大会上，Google正式宣布热门休闲游戏Angry Birds(愤怒的小鸟）已正式进入Chrome Web Store平台，任何 Chrome 用户都可以免费下载安装(或者访问chrome.angrybirds.com)，这也意味着你可以 在 Ubuntu/Linux 平台上来玩这款游戏了.
愤怒一把，小鸟折纸
- maajiaa - 设计｜生活｜发现新鲜好吧，落俗一次，谁让现在小鸟们这么火呢. 如果你不知道angry birds，不好意思，动动手指，这里就不帮您扫盲啦. 现在Adrian Aka(Little Plastic Man)为大家创作了这套逼真的纸模，更伟大的是，他提供了所有图纸供大家下载，大家不用去购买昂贵的周边了，打印下来，准备好剪刀胶水，当个DIY达人，做一套属于你的小鸟们.
愤怒小鸟蛋黄莲蓉月饼
- Zoe - 煎蛋这……中秋节快到了，各种为了圈钱而生出的月饼应运而生. 去年这个时候，我去领了一盒传说中的哈根达斯月饼（打开看，其实就是酥皮冰淇淋）. 现在由于小鸟游戏的火爆，我们在香港，估计在国内也能看到，这种愤怒小鸟蛋黄莲蓉月饼. @oioi：所以Angry Birds Season 版本是不是应该果断出一个中秋节版本.
元首的愤怒之PPT方案版
- satan - 乐淘吧[视频]元首的愤怒-卡农神曲. 两元首看美女胸，另两个看美女屁股，奥巴马和卡梅伦做一本正经状. » 非特殊声明，本站所有图片，文字，视频皆来源于网络，如有侵权，请告知乐淘吧. 转载请注明来源：乐淘吧 » 《元首的愤怒之PPT方案版>>
》. » 本文链接地址：http://letaoba.info/2011/08/humor/5006.html.
愤怒的小鸟，Twitter 打官司
- SotongDJ - 爱范儿 · Beats of Bits这里，愤怒的小鸟不是某热门游戏的主角，而是广为使用的服务：Twitter. 近日它恼羞成怒，开始向第三方发起诉讼. 从 Tweet 被权威字典收录说起. 2009年，因为 Twitter 的广泛使用 Tweet 一词作为 Twitter 的动词形式一同被收录在《柯林斯英文词典》30周年版中. 也就是从这个时候起，Tweet 得到了包括牛津，韦氏字典在内的权威字典认证.
【无语了】愤怒的猪猪：Hungry Piggy
- 貝殼 - 爱Apps - www.iapps.im精选限时免费应用，由 AppPusher 为您送达. 无限精彩，尽在 爱Apps - www.iapps.im. 本站原创内容，转载时请务必注明出处，谢谢. 大小: 17.8 MB
系统: 3.1.3+. 感谢”咕嘟咕嘟“在”爱分享“中留言分享. 截图中就已经找到海贼王、火影忍者、冒险岛的影子了，更别提Hungry Piggy和那独特的首页风格.
现实版愤怒的小鸟
- Kidwind - 玩意儿愤怒的小鸟和植物大战僵尸两个神级趣味游戏相信都有接触过吧，在这里艺术家 Mohamed Raoof 将里面的鸟儿现实化，看看一个个愤怒的表情. 本文原始链接：http://www.cngadget.cn/angry-birds-2.html.