盘点数学里十大不需要语言的证明
- Esperisto - 果壳网 guokr.com - 果壳网当谈到复杂数学定理的证明时，很多人常常为之色变，认为这只是一个枯燥的公式堆砌和深奥的数学推导过程. 这当然是一个让笔者感到纠结的误解. 因为数学证明中包含的美丽与精巧实在是一道亮丽的风景线，而这种亮丽甚至不需要用语言来描述. 所以我在这里盘点了数学里十大不需要语言的证明（poofs without words）.
盘点数学里十大不需要语言的证明
标签：
盘点
数学
需要
| 发表时间：2011-08-10 12:06 | 作者：(author unknown) Esperisto
出处：http://www.guokr.com/
当谈到复杂数学定理的证明时，很多人常常为之色变，认为这只是一个枯燥的公式堆砌和深奥的数学推导过程。这当然是一个让笔者感到纠结的误解。因为数学证明中包含的美丽与精巧实在是一道亮丽的风景线，而这种亮丽甚至不需要用语言来描述。所以我在这里盘点了数学里十大不需要语言的证明（poofs without words）。让读者在领略数学所包含的无与伦比的精巧之外，更从此爱上数学。
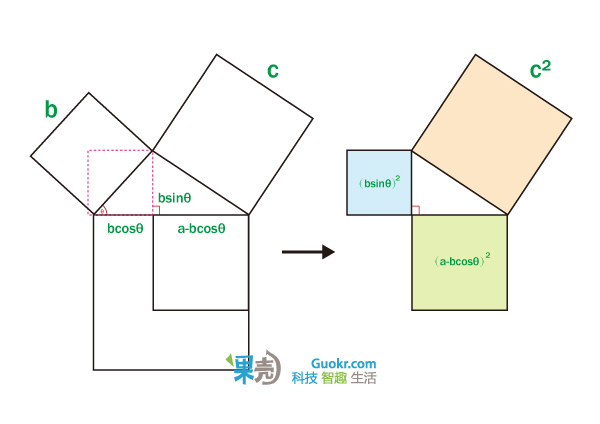
0. 勾股定理
这个大家小学就学过的古老定理，有着无数传奇故事。我可以很随意的写出她的10个不同的证明方法。而路明思（Elisha Scott Loomis）在 《毕达哥拉斯命题》（ Pythagorean Proposition）提到这个定理的证明方式居然有367种之多，实在让人惊讶。这里给出一个不需要语言的证明方法。
实际上勾股定理是余弦定理的一种特殊情况，而余弦定理的证明，同样可以不用语言。
1. 关于反正切的恒等式
关于反正切，有如下两个很精彩的等式：
arctan1/2+arctan1/3=π/4 acrtan1+arctan2+arctan3=π
它们的证明方法也同样精彩
2. 几何平均值小于算术平均值
这是不等式中最重要和基础的等式：
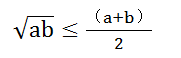
它也可以通过图形来证明。
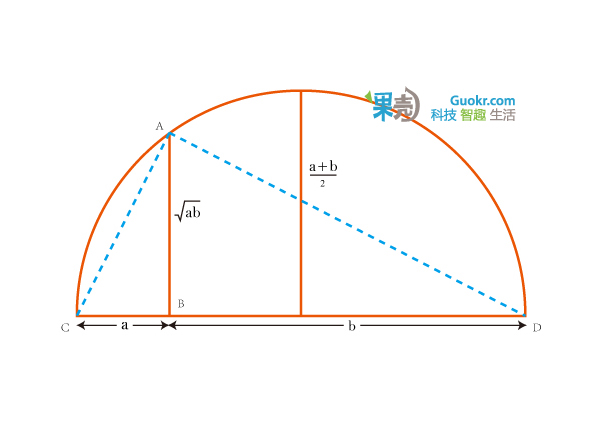
注意到△ABC∽△DBA ,可以很轻松地得到AB=√ab。剩下的就显而易见了。
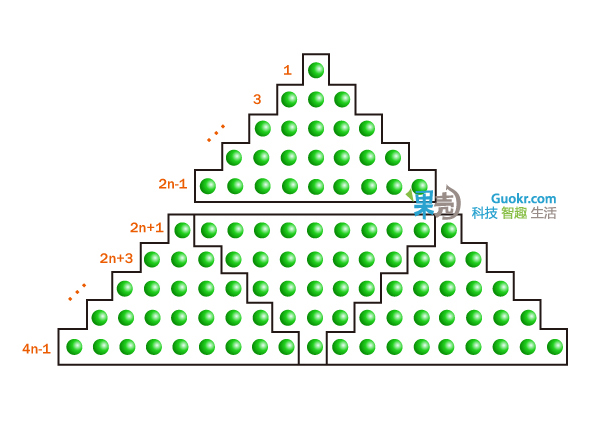
3. 1+3+5+…+（2n-1）= n 2
这是奇数的求和公式，下图是当n=8时的情形
4. 平方数的求和公式
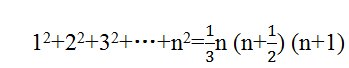
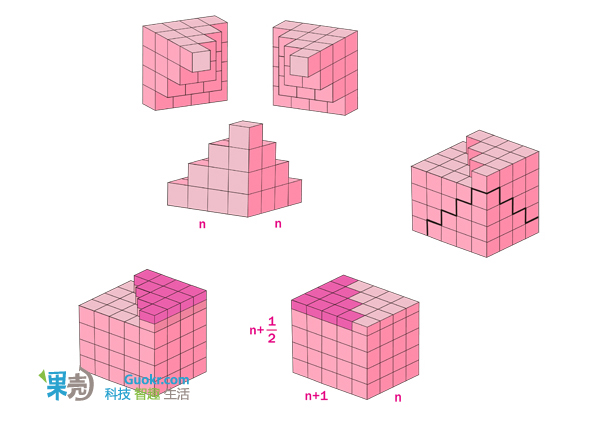
5. 立方数的求和公式
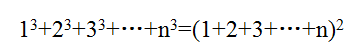
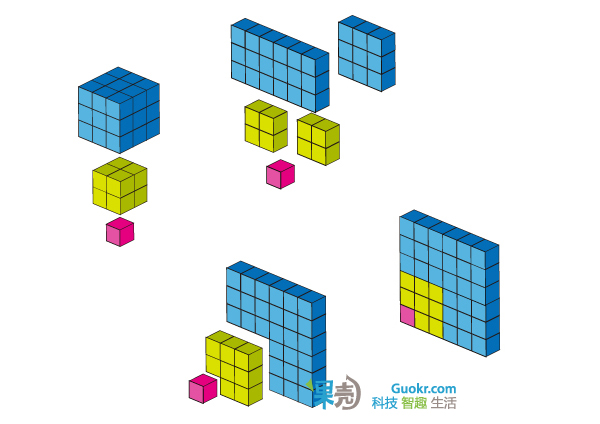
6. 斐波那契数列的恒等式
可谓家喻户晓的斐波那契数列指的是这样一个数列：1、1、2、3、5、8、13、21 ……
这个数列从第三项开始，每一项都等于前两项之和， F n+1 = F n + F n-1 。
它的通项公式是
有趣的是，这样一个完全是自然数的数列，通项公式居然是用无理数来表达的。而且当n无穷大时 F n-1 / F n 越来越逼近黄金分割数0.618。正因为它的种种神奇性质，美国数学会甚至从1960年代起出版了《斐波纳契数列》季刊。关于斐波那契数列，有一个恒等式是这样的
这个等式很漂亮，不需要借助复杂的数学推导，它有一个很直观的证明方法
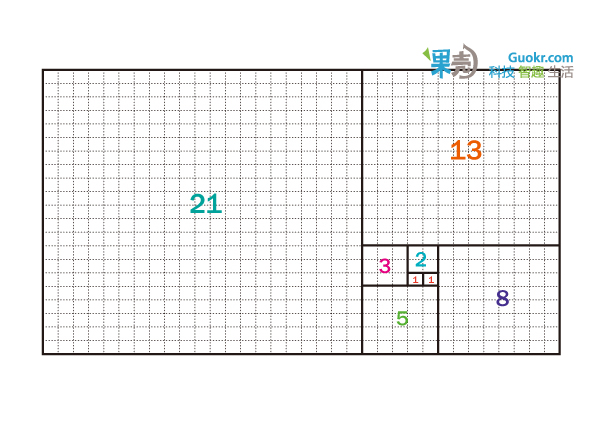
7. 结果为1/3的一组分子式
下面是一组分子式，他们的结果都等于1/3 ：
8. 最受数学家喜爱的无字证明
1989 年的《美国数学月刊》（American Mathematical Monthly）上有一个貌似非常困难的数学问题：下图是由一个个小三角形组成的正六边形棋盘，现在请你用右边的三种（仅朝向不同的）菱形把整个棋盘全部摆满（图中只摆了其中一部分），证明当你摆满整个棋盘后，你所使用的每种菱形数量一定相同。
《美国数学月刊》提供了一个非常帅的“证明”。把每种菱形涂上一种颜色，整个图形瞬间有了立体感，看上去就成了一个个立方体在墙角堆叠起来的样子。三种菱形分别是从左侧、右侧、上方观察整个立体图形能够看到的面，它们的数目显然应该相等。
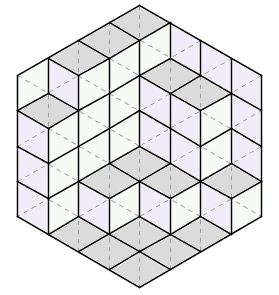
它把一个纯组合数学问题和立体空间图形结合在了一起，实在让人拍案叫绝。这个问题及其鬼斧神工般的“证明”流传甚广，深受数学家们的喜爱。死理性派曾经讨论过 这个问题 。同时它还是死理性派logo的出处。
9. 棋盘上的数学证明
在一个8×8的国际象棋棋盘上，我们可以用32张多米诺骨牌（是两个相连正方形的长方形牌）覆盖整个棋盘上的64个方格。如果将对角线上的两个方格切掉，剩下来的62个格子还能用31张骨牌覆盖住吗？
答案是不能的。每一张骨牌在棋盘上必是覆盖住两个相邻方格，一白一黑。所以31张骨牌应该可以盖住31个黑格和31个白格。而这被切了角的棋盘上的方格有32个是一种颜色，另一种颜色是30个，因此是不能被31张骨牌覆盖的。
但是如果我们切掉的不是颜色相同的两个呢？假如我们从棋盘的任何部位切掉两个颜色不同的方格，那么剩下来的62格是否一定能被31张骨牌完全盖住？我可以告诉你这是一定能做到的,并且关于这个结论，存在一个非常漂亮的证明。建议读者在继续往下阅读前，可以先自行思考如何证明这个结论。
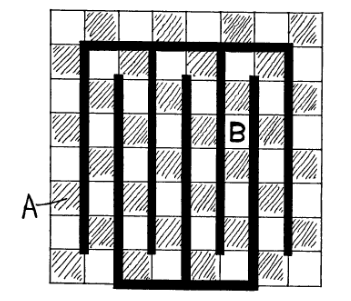
上图就是那个漂亮的证明。不妨对它再赘述两句。粗黑线条将整个棋盘转变为一条首尾相连、黑白格相间的封闭路线。从这棋盘上切掉任何两个颜色不同的方格，会让这个封闭线路变成两段线路（如果切掉的方格是相连的，那就是一条线路）。在这两段（或一段）线路中，两种颜色的格子数量都是偶数，故分别都可以被若干张骨牌覆盖。从而证明整个棋盘可以被31张骨牌完全覆盖。
这个著名的棋盘问题是数学游戏大师马丁•加德纳提出的，而上述精妙绝伦的证明则是数学家哥莫瑞（Ralph Gomory）找到的。它们后来被收录在《意料之外的绞刑和其他数学娱乐》这本书里。
数学里，有一种证明方法叫做Proofs without words。诚然，这种证明方法算不上严格，但是它却将数学中包含的最精巧的东西一览无余地展现了出来。本文列举了十个经典的例子。你还见过什么高明的吗，可以在回帖中写出来。如果有很漂亮的，我会在这里推荐出来。
资料来源：
《意料之外的绞刑和其他数学娱乐》
《Proofs without words》
相关 [盘点 数学 需要] 推荐：
盘点：iOS未来版本需要解决的20件事（上）
- - 最科技 | 关注互联网科技与应用创新的TMT媒体【最科技讯】下一代iPhone和iPad将运行iOS 7. 上一个版本 iOS 6拥有200多项新功能，但这些新功能来未曾在野外测试就进行运行，以至于出现了许多错误和缺陷. 苹果移动操作系统的再次更新，可能还将出现许多缺陷和问题，并导致用户没完没了的抱怨，甚至拖垮苹果品牌的信誉. iOS 7预计将在6月中旬的苹果全球开发者大会（WWDC）上公布，今年在美国加州举行，届时将有多项新功能和服务亮相.
UI设计需要什么软件—UI设计常用软件盘点
- - 酷勤网-挖经验 [expanded by feedex.net] 来源：365UCD 2012-01-04. UI设计，即用户界面设计，是对软件的人机交互、操作逻辑、界面美观的整体设计，UI设计不是单纯的美术绘画，他需要定位使用者，使用环境，使用方式并为最终用户而设计. 本文将为大家盘点一些UI设计的常用软件，供初学者参考. Photoshop并非一个单纯的图像编辑软件，它的应用领域涉及图像、图形、文字、视频、出版等各个方面，非常广泛.
随记：我们需要怎样的数学教育？
- rangerqu - Matrix67: My Blog 注：这篇文章里有很多个人观点，带有极强的主观色彩. 其中一些思想不见得是正确的，有一些话也是我没有资格说的. 我只是想和大家分享一下自己的一些想法. 我是一个纯粹打酱油的数学爱好者，只是比一般的爱好者更加执着，更加疯狂罢了. 初中、高中一路保送，大学不在数学专业，这让我可以不以考试为目的地学习自己感兴趣的数学知识，让我对数学有如此浓厚的兴趣.
编程需要知道多少数学知识？
- - 博客 - 伯乐在线下面是我在reddit的子论坛 r/learnprogramming 看到的几个帖子:. ● “ 要成为一个优秀的程序员需要学习多少数学. ● “ 我应该重新学习数学吗. ● “ 这可能是我提问过的最愚蠢的一个问题. 成为一个优秀的程序员究竟需要学习多少数学. 数学和编程有一种容易让人误解的联系.
想爬得更高，需要知道的数学体系
- - 博客园_知识库 在过去的一年中，我一直在数学的海洋中游荡，research进展不多，对于数学世界的阅历算是有了一些长进. 作为计算机的学生，我没有任何企图要成为一个数学家. 我学习数学的目的，是要想爬上巨人的肩膀，希望站在更高的高度，能把我自己研究的东西看得更深广一些. 说起来，我在刚来这个学校的时候，并没有预料到我将会有一个深入数学的旅程.
转型AI产品经理，原来不需要学那么深的算法和数学模型
- - IT瘾-tuicool本文作者李杰克 是我们“AI产品经理大本营”成员，但非常特别是，他是 从互联网产品经理转型成了AI工程师. 李杰克 文章的特点，是 能 通过简单有趣的文字介绍AI技术概念，本文是他的第一篇文章，以飨大家. 这是我的第一篇文章，如果你还没系统地学习过AI算法相关知识，它应该能够让你对AI有些新的认知和理解、多些信心，至少你不会再觉得AI是那么高不可攀、遥不可及，相反，AI是普通人也可以理解、学习和实现的.