经典证明：等边三角形内一点到各顶点的距离长可构成一个三角形

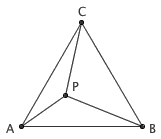
    这是初中平面几何的一个经典问题：等边三角形 ABC 内有任意一点 P，求证 PA 、 PB 、 PC 的长度一定能构成一个三角形。

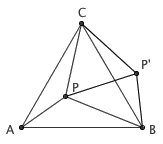
    这里给出两种证明方法。传统的证明方法是，把 △CPA 绕着点 C 逆时针旋转 60 度，从而旋转后的 CA 将会和 CB 重合，同时 P 点落在了 P' 的位置。由于 △CP'B 是由 △CPA 旋转过去得到的，因此 P'B = PA 。另外，线段 CP' 是 CP 绕着点 C 旋转 60 度得到的，说明 CP 和 CP' 长度相等且夹角为 60 度，即 △CPP' 是等边三角形，于是 PP' = CP 。那么， △BPP' 的三边长事实上分别等于 PA 、 PB 、 PC ，命题得证。

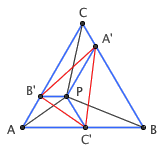
    今天我学到了另外一种证明方法，看上去更简洁巧妙一些。过点 P 分别作三边的平行线，将整个三角形划分为三个蓝色四边形。那么，图中的三个蓝色四边形都有一组对边平行，因而他们都是梯形；事实上，容易看出，这些梯形的两个底角都是 60 度，因而他们都是等腰梯形。只需注意到，等腰梯形的两条对角线长度是相等的，因此红色三角形 A'B'C' 的三边长度事实上就分别等于 PA 、 PB 、 PC ，命题得证。

来源：http://www.cut-the-knot.org/Curriculum/Geometry/Pompeiu2.shtml