e,一个常数的传奇
来自: 死理性派 - 果壳网 - FeedzShare www.guokr.com - FeedzShare
发布时间:2011年07月27日, 已有 2 人推荐
自然对数的底e是一个令人不可思议的常数,一个由lim (1+1/n) n 定义出的常数,居然在数学和物理中频频出现,简直可以说是无处不在。这实在是让我们不得不敬畏这神奇的数学世界。
欧拉恒等式
但凡说起e,一个必定要提到的公式就是欧拉恒等式——被誉为世界上最美丽的公式。
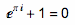
数学中最基本的5个常数——0、1、圆周率π、自然对数的底e和虚数单位i,以及数学中最基本的两个符号,等号和加号,就这样通过一个简单的恒等式联系在了一起,实在是让人叹服。
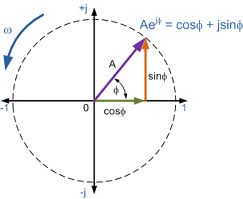
这个等式有个一几何的直观解释。一个实数在实数轴上可以用一个向量表示,旋转这个向量,就相当于乘以一个虚数i。据此建立一个以实数为横轴,虚数为纵轴的坐标系。实单位向量,每次逆时针旋转π/2, 可以分别得到结果1,i,-1,-i,1. 即转4次以后就回到了原位。而当实单位向量保持长度不变旋转θ角度,得到的向量就是:cosθ+isinθ。根据欧拉公式 e iθ = cosθ+isinθ可以看出 e iθ 就代表实单位向量1旋转θ角后而得到的向量。所以 e iπ 意味着单位向量逆时针旋转了π,结果显然是-1。
增长规律
这个世界上有许许多多的事物满足这样的变化规律:增长率正比于变量自身的大小。例如放射性元素衰变的时候,衰变率就和现存的放射性物质多少成正比;资源无穷多的社会,人口出生率将(近似的)和现存人口数成正比等等。而此类变化规律所确定的解,则是由以e为底的指数增长所描述的:如果x的变化率等于变量x自身的λ倍,那么该变量随时间t的函数则为
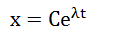
其中C是任意常数。而e的直观含义正是增长的极限,这个问题在 数学常数e的含义 中有过详细的介绍。
正态分布
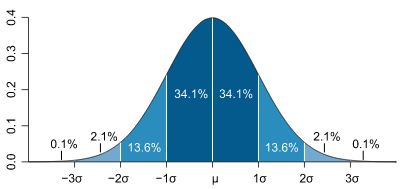
正态分布是自然科学与行为科学中的定量现象的一个统计模型。各种各样的心理学测试分数和物理现象比如光子计数都被发现近似地服从正态分布,尽管这些现象的根本原因经常是未知的。而理论上则可以证明如果把许多小作用加起来看做一个变量,那么这个变量服从正态分布。
正态分布在生活中也可谓是无处不在。多次反复测量一个物理量,测出来的值一般来说总是呈正态分布;瓶装可乐的实际体积,也是正态分布;一大群人的寿命分布、智商分布等,也都是正态分布。而正态分布的表达式中,也神奇的出现了e。
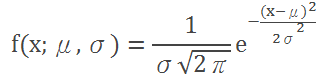
伽马函数与斯特林公式
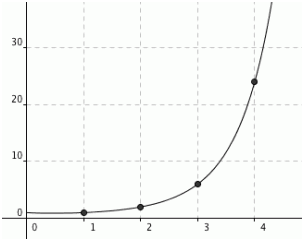
阶乘运算n!本来是定义在正整数上的。数学家最爱做的事情就是推广,因此阶乘函数自然不能幸免。当把阶乘函数推广到定义域为复数的时候,我们要寻找的函数就是一条通过了所有(n+1,n!)点的函数。所谓的伽马函数Γ(x)满足了这个性质,而伽马函数的表达式中又出现了e:
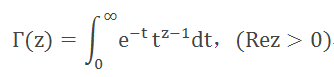
阶乘n!与e还有另一层神秘的联系。
当n趋于无穷大的时候,n!满足下面的近似关系式——斯特林公式:
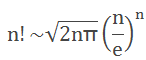
(其中“~”符号表示同阶,可以大致认为是n趋于无穷大时的约等于)
要计算很大的阶乘值,位数受限而不能直接用计算机求出时,就可以用斯特林公式近似求出了。
调和级数
所谓调和级数级数,即1+1/2+1/3+1/4+…+1/n+...。它是一个发散级数,当n趋于无穷大的时候,这个和也将趋于无穷大。但是同样是发散的级数,发散也有快慢之分。调和级数发散速度是怎样的呢?伟大的欧拉发现的一个著名极限给出了答案:

因此调和级数的发散速度正是和以e为底的对数——ln函数的发散速度一致。
素数与e
素数(或称质数)是指除了1和它本身之外,无法被其他自然数整除的数。素数看似和e毫无联系,可是,素数分布的理论指出,素数的分布与e息息相关。如果用π(x)表示不大于x的素数个数(注意这里的π不是圆周率!),那么素数分布中心定理指出

或者可以写成
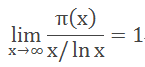
注意到ln正是以e为底的对数。看,e就这样出现在了看似毫无关系的领域!
悬链线
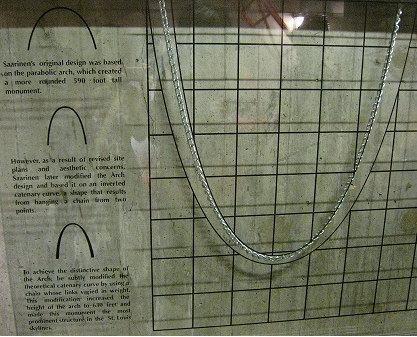
数学史上曾经有一个著名问题,称之为悬链线问题:一根柔软不可伸长的链子,两头固定在空间中的两个定点上(这两个点不一定要等高),链子形成的曲线是怎样一条曲线呢?这个问题和最速降线问题提出的时间很接近,而且参与者也大多相同。早在文艺复兴时代它就已经被达芬奇研究过,可惜并没有得到答案。伽利略猜想答案是抛物线,这也和很多人最初的感觉是一致的,可惜后来被惠更斯在17岁的时候证明是错的。
和最速降线问题一样,这一问题伯努利兄弟中的一个也曾公开征集解答,不过这次是哥哥雅各布,他在1690年的《教师学报》中发表了这个问题。在雅各布提出这一问题一年后的1691年6月,《教师学报》发表了惠更斯(当时已经62岁)、莱布尼茨以及约翰•伯努利提交的三份正确答案。三人的方法都不一样,但最终的结果却是一致的。而雅各布自己则并没能把它解出来,这让弟弟约翰•伯努利异常兴奋。
悬链线的正确方程是这样的:
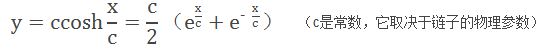
它的发现在当时被看做是新微积分伟大成果的重要标志。而现在,悬链线则在世界著名的标志性建筑物——密苏里的圣路易斯大拱门——中永垂不朽了。

e一次次如幽灵般恰当的出现在了每一处,时常给人们带来惊喜。而上述这些,只不过它的冰山一角而已。

