Wand 算法介绍与实现
本文主要介绍 Wand(Weak And) 算法的原理和实现, Wand 算法是一个搜索算法,应用在 query 有多个关键词或标签,同时每个document 也有多个关键词或标签的情形(如搜索引擎);尤其是在 query 中的关键词或标签较多的时候,通过 Wand 能够快速的选择出 Top n 个相关的 document,算法的原始论文见 Efficient Query Evaluation using a Two-Level Retrieval Process,本文主要讲述这个算法的原理以及通过 python 实现这个算法。
一般来说,检索往往会利用倒排索引,倒排索引能够根据 query 中的关键词快速检索到候选文档,然而当候选文档集合较大时,遍历整个候选文档所需要的时间也很大。
但是检索需要得到的往往只是 Top n 个结果,在遍历候选文档过程中能否跳过一些与 query 相关性较低的文档,从而加速检索的过程呢?Wand 算法就是干这个事的。
Wand 原理介绍
Wand 算法通过计算每个词的贡献上限来估计文档的相关性上限,并与预设的阈值比较,进而跳过一些相关性一定达不到要求的文档,从而得到提速的效果。
上面这句话涵盖了Wand 算法的思想,下面进行详细说明:
Wand 算法首先要估计 每个词对相关性贡献的上限(upper bound),最简单的相关性就是 TF-IDF,一般IDF是固定的,因此只需要估计一个词在各个文档中的词频TF上限(即这个词在各个文档中最大的TF),该步骤通过线下计算即可完成。
线下计算出各个词的相关性上限,可以计算出 一个 query 和一个文档的相关性上限值,就是他们共同出现的词的相关性上限值的和,通过与预设的阈值比较,如果query 与文档的相关性大于阈值,则进行下一步的计算,否则丢弃。
在上面过程中,如果还是将 query 和一个一个文档分别计算相关性,并没有减少时间复杂度, Wand 算法通过一种巧妙的方式使用倒排索引,从而能够跳过一些相关性肯定达不到要求的文档。
Wand 算法步骤如下
- 建立倒排索引,记录每个单词所在的所有文档ID(DID),ID 按照从小到大排序
- 初始化 posting 数组,使得 posting[pTerm] 为词 pTerm 倒排索引中第一个文档的 index
- 初始化 curDoc = 0(文档ID从1开始)
接着可以执行下面的 next 函数(摘自原始论文),

上面流程中用到的几个函数的含义如下
1. sort(terms, posting):根据 posting 数组指向的当前文档 ID,对所有的 terms 从小到大排序。如下是三个 term 及其对应的索引文档的 ID,此时的 posting 数组为 [1, 0, 1], 则根据各个 term 当前文档 ID 排序的结果应该是 t1, t2, t3
t0: [3, 26]
t1: [ 4, 10, 100]
t2: [2, 5, 56]
2. findPivotTerm(terms, θ):按照之前得到的排序,从第一个 term 开始累加各个 term 的相关性贡献的上限(upper bound,UB),这个在之前已经通过离线计算出来;直到累加和大于等于设定的阈值 θ, 返回当前的 term。这里应用 这篇文章的一个例子,下面为通过 sort(terms, posting) 后的倒排索引,假设阈值 θ = 8
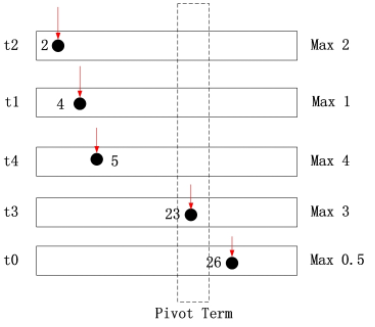
对于doc 2,其可能的最大得分为2<8 对于doc="" 4,其可能的最大得分为2+1="3<8" 5,其可能的最大得分为2+1+4="7<8" 23,其可能的最大得分为2+1+4+3="10">8
因此,t3 为pivotTerm,doc 23 为pivot
3. pickTerm(terms[0..pTerm]):在0到pTerm(不包含pTerm)中选择一个term,关于选择策略,当然是以 可以跳过最多的文档为原则,论文中选择了 IDF 最大的term。以上面的图为例子,此时可以选择 t2, t1 或 t4, 根据其 IDF 值选择最大的 term 即可
4. aterm.iterator.next(n):返回 aterm 这个单词对应的倒排索引中的文档ID(DID),这个DID要满足DID >= n。则 posting[aterm] ← aterm.iterator.next(n) 其实就是更新了 aterm 在 posting 数组中的当前文档,从而跳过 aterm 对应的索引中一些不必要计算的文档。
还是以上面的图为例子,假如选择的 aterm 为 t2, 则 t2 中指向 2 的指针要往后移动直至 DID >= 23 ,这样便跳过了部分不必计算文档。
实际上,t1, t4 也可以执行上面这个操作,因为在 doc 23 之前的 doc 的得分不可能达到阈值 θ(因为 DID 是经过排序的) ,所以t2、t1、t4对应的 posting 数组中的项都可以直接跳到大于等于doc23的位置,但是论文中每次只选择一个 term ,虽然多迭代几次也能达到同样效果,但是我认为这里可以三个 Term 可以一起跳。
介绍了上面过程中几个重要函数,下面来看一下上面的几个分支分别表示情况
-
if (pTerm = null) return (NoMoreDocs)表示当前所有 term 的 upper bound 和达不到阈值 θ ,结束算法 -
if (pivot = lastID) return (NoMoreDocs)表示当前已经没有满足相关性大于阈值 θ 的文档,结束算法 -
if (pivot ≤ curDoc)表示当前 pivot 指向的 DID 已经计算过相关性,需要跳过,这部分代码会在下面第4步执行后在进入循环时执行 -
if (posting[0].DID = pivot)表示当前 pivot 对应的文档的相关性有可能满足大于阈值 θ ,返回这篇文档的 ID 并计算这篇文档和 query 的相关性;posting[0].DID = pivot表示从第一个term到当前的term所指向的文档都是同一篇 -
if (posting[0].DID = pivot) 对应的else语句表示前面遍历过的那些 term 的当前 DID 都不可能满足大于阈值 θ,因此需要跳过,也正是这里大大减少了需要计算相关性的文档数量
Wand 的实现代码
实现 Wand 算法的 Python 代码见 这里,参考 这篇文章的代码进行了修改,并增加了评估文档和query相似性的函数,代码中有以下几点需要注意
- 当一个 term 对应的所有 document 遍历完后,有两种处理方法。第一种方法是直接删除,这样会降低每次排序的时间复杂度和内存占用率,但是每次删除时候是要在一个有序列表内删除,时间复杂度为 $O(n)$, $n$ 为 terms 的个数;第二种方法是在每个 term 的 document list 最后增加一个比所有文档ID都要大的数(LastID),这样被遍历完的term会自然被排序到最后,整个代码更加简洁。两种方法都尝试了一下,详细代码可见上面的代码连接的提交历史
-
pickTerm方法原论文采用的是选择 idf 最大值的term,这里直接选择第一个,因为代码仅用于阐述算法的流程,各个 term 没有 idf 值。当然,如果有各个 term 的 idf 值,是可以根据 idf 选择的 - 上面伪代码的算法流程中最后的 else 语句是选择 pivotTerm 中的任意一个并跳过相关性低的文档,但是从前面的解释可知,可以 pivotTerm 前面的所有 term 都可进行这一操作,因此代码里面的这部分跟伪代码不同
这里还是给出完整代码,可以对照着上面的伪代码看,命名方法基本都保持了一致,如有错漏,欢迎指出
1 | import heapq |
参考资料