背景：什么是LSA?

Latent Semantic Analysis（LSA）中文翻译为潜语义分析，也被叫做Latent Semantic Indexing ( LSI )。意思是指通过分析一堆（不止一个）文档去发现这些文档中潜在的意思和概念，什么叫潜在的意思？我第一次看到这个解释，直接懵逼。其实就是发现文档的中心主题吧？假设每个词仅表示一个概念，并且每个概念仅仅被一个词所描述，LSA将非常简单（从词到概念存在一个简单的映射关系）。

根据常识我们知道两个很常见的语言现象：1. 存在不同的词表示同一个意思（同义词，吃饭 & 就餐）；2. 一个词表示多个意思（一词多义， 苹果【水果】 & 苹果 【公司】）。这种二义性（多义性）都会混淆概念以至于有时就算是人也很难理解。

---

LSA工作原理

潜语义分析（Latent Semantic Analysis）来源于信息检索（IR）中的一个问题：如何从搜索query中找到相关的文档。有的人说可以用关键词匹配文档，匹配上的就放在搜索结果前面。这明显是有问题滴，一是背景里我们讲过一词多义和同义词问题，二则10亿+的文档采用关键词匹配，实在不现实。

其实呀，在搜索中我们实际想要去比较的不是词，而是隐藏在词之后的意义和概念，用人话说：query搜索的结果文档隐含的概念要和query的概念尽可能的相近。LSA分析试图去解决这个问题，它把词和文档都映射到一个”概念”空间并在这个空间内进行比较（注：也就是一种降维技术）。

当文档的作者写作的时候，对于词语有着非常宽泛的选择。不同的作者对于词语的选择有着不同的偏好，这样会导致概念的混淆。这种对于词语的随机选择在 词-概念 的关系中引入了噪音。LSA滤除了这样的一些噪音，并且还能够从全部的文档中找到最小的概念集合（为什么是最小？）。

为了让这个难题更好解决，LSA引入一些重要的简化：

• 文档被用BOW( bags of words : 词袋 )表示，因此词在文档中出现的位置并不重要，只有一个词的出现次数。
• 概念被表示成经常出现在一起的一些词的某种模式。有点想KNN的思想，文档中概念A相关的词出现次数最多，就把这个文档映射到概念A。例如：4k屏幕、8核CPU 、4G RAM ……经常出现在手机广告文档中。
• 词被认为只有一个意思。但是这可以使得问题变得更加容易。（这个简化会有怎样的缺陷呢？）

---

LSA能彻底解决文档映射到概念这个问题吗？

NO！ NO ！NO！ LSA只能很好的应对，并不能解决。一方面是因为文档长度，语法结构，用词规范，各种问题的限制 ，一句话，NLP 太复杂了；另一方面是LSA本身的问题。

---

LSA实现步骤

文档预处理

对文档分词，词根还原（en），去停用词，保留索引词（index word），删除特殊符号等。

索引词可以是满足下面条件的词：

• 不是那种特别常见的词，例如 “and”, ”the” 这种停用词（stop word）。这种词没有包含进来是因为他们本身不存在什么意义。
• 在2个或者2个以上文档里出现。

例子：在amazon.com上搜索”investing”(投资) 并且取top 10搜索结果的书名。下面就是那9个标题，索引词（在2个或2个以上标题出现过的非停用词）被下划线标注:

1. The Neatest Little Guideto Stock Market Investing
2. InvestingFor Dummies, 4th Edition
3. The Little Bookof Common Sense Investing: The Only Way to Guarantee Your Fair Share of Stock MarketReturns
4. The Little Bookof Value Investing
5. Value Investing: From Graham to Buffett and Beyond
6. Rich Dad’s Guideto Investing: What the Rich Invest in, That the Poor and the Middle Class Do Not!
7. Investing in Real Estate, 5th Edition
8. Stock InvestingFor Dummies
9. Rich Dad’sAdvisors: The ABC’s of Real Estate Investing: The Secrets of Finding Hidden Profits Most Investors Miss

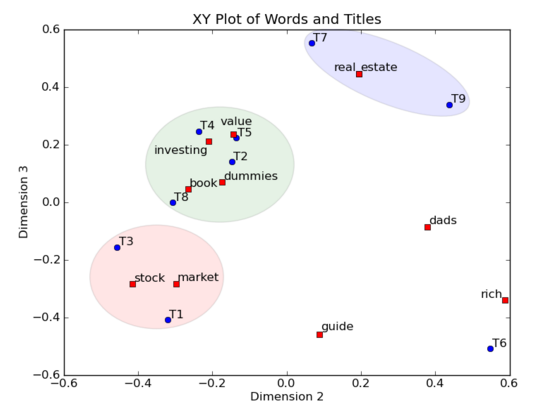
在这个例子里面应用了LSA，在XY轴的图中画出词和标题的位置（只有2维），并且识别出标题的聚类。蓝色圆圈表示9个标题，红色方块表示11个索引词。我们不但能够画出标题的聚类，并且由于索引词可以被画在标题一起，我们还可以给这些聚类打标签。例如，蓝色的聚类，包含了T7和T9，是关于real estate（房地产）的，绿色的聚类，包含了标题T2，T4，T5和T8，是讲value investing（价值投资）的，最后是红色的聚类，包含了标题T1和T3，是讲stock market（股票市场）的。标题T6是孤立点（outlier）。

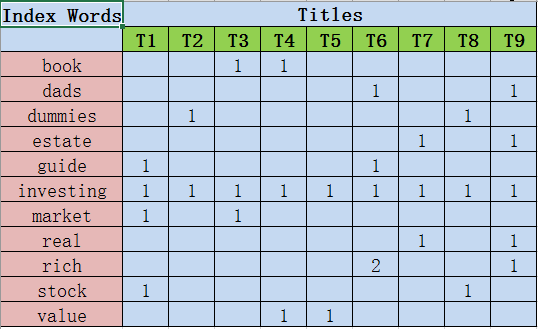
创建词到文档的矩阵

在这个矩阵里，每一个索引词占据了一行，每一个文档占据一列。每一个单元（cell）包含了这个词出现在那个文档中的次数。例如，词”book”出现在T3中一次，出现在T4中一次，而” investing”在所有标题中都出现了一次。一般来说，在LSA中的矩阵会非常大而且会非常稀疏（大部分的单元都是0）。这是因为每个标题或者文档一般只包含所有词汇的一小部分。更复杂的LSA算法会利用这种稀疏性去改善空间和时间复杂度。

代码实现

在这篇文章中，我们用python代码去实现LSA的所有步骤。我们将介绍所有的代码。Python代码可以在这里被下到（见上）。需要安装NumPy 和 SciPy这两个库。

NumPy是python的数值计算类，用到了zeros（初始化矩阵），scipy.linalg这个线性代数的库中，我们引入了svd函数也就是做奇异值分解 , LSA的核心。string是python自带的库，我们用到string.punctuation，包含文档中的特殊符号。

      In [1]:importstring
In [2]:printstring.punctuation
!"#$%&'()*+,-./:;<=>?@[\]^_`{|}~

导入Python 包

      # -*- coding: utf-8 -*-"""
Created on Fri Jun 17 15:42:40 2016

@author: zang
"""fromnumpyimportzerosfromscipy.linalgimportsvdimportstring

定义LSA类

      classLSA(object):def__init__(self, stopwords, ignorechars):self.stopwords = stopwords
    self.ignorechars = ignorechars
    self.wdict = {}
    self.dcount =0

定义一个LSA类，wdict字典用来记录词的个数，dcount用来记录文档号。

解析文档

      defparseDoc(self, doc):words = doc.split()forwinwords:
       w = w.lower().translate(None, self.ingorechars).strip()# 去除特殊字符ifw =="":continueelifwinself.stopwords:continueelifwinself.wdict:
         self.wdict[w].append(self.dcount)else:
         self.wdict[w] = [self.dcount]
    self.dcount +=1

在LSA类里添加这个函数。这个函数就是把文档分词，并滤除停用词和标点，剩下的词会把其出现的文档号填入到wdict中去，例如，词book出现在标题3和4中，则我们有self.wdict[‘book’] = [3, 4]。相当于建了一下倒排。

建立索引词文档矩阵

      defbuildMwd(self):self.keys = [kforkinself.wdict.keys()iflen(self.wdict[k]) >1]   
    self.keys.sort()   
    self.Mwd = zeros([len(self.keys), self.dcount])fori, kinenumerate(self.keys):fordinself.wdict[k]:  
        self.Mwd[i,d] +=1

所有的文档被解析之后，所有出现的词（也就是词典的keys）被取出并且排序。建立一个矩阵，其行数是词的个数，列数是文档个数。最后，所有的词和文档对所对应的矩阵单元的值被统计出来。

打印索引词文档矩阵

      defprintMwd(self):printself.Mwd

打印出索引词文档矩阵。

测试LSA类

      if__name__ =="__main__":
    docs =\
    ["The Neatest Little Guide to Stock Market Investing","Investing For Dummies, 4th Edition","The Little Book of Common Sense Investing: The Only Way to Guarantee Your Fair Share of Stock Market Returns","The Little Book of Value Investing","Value Investing: From Graham to Buffett and Beyond","Rich Dad's Guide to Investing: What the Rich Invest in, That the Poor and the Middle Class Do Not!","Investing in Real Estate, 5th Edition","Stock Investing For Dummies","Rich Dad's Advisors: The ABC's of Real Estate Investing: The Secrets of Finding Hidden Profits Most Investors Miss"]

    stopwords = ['and','edition','for','in','little','of','the','to'] 
    ignorechars = string.punctuation
    lsaDemo = LSA(stopwords,ignorechars)fordindocs:
        lsaDemo.parseDoc(d)
    lsaDemo.buildMwd()
    lsaDemo.printMwd()

在刚才的测试数据中验证程序逻辑，并查看最终生成的矩阵：

      In [33] : runfile('G:/Python/nlp/LSA.py', wdir='G:/Python/nlp')
[[0.0.1.1.0.0.0.0.0.]
 [0.0.0.0.0.1.0.0.1.]
 [0.1.0.0.0.0.0.1.0.]
 [0.0.0.0.0.0.1.0.1.]
 [1.0.0.0.0.1.0.0.0.]
 [1.1.1.1.1.1.1.1.1.]
 [1.0.1.0.0.0.0.0.0.]
 [0.0.0.0.0.0.1.0.1.]
 [0.0.0.0.0.2.0.0.1.]
 [1.0.1.0.0.0.0.1.0.]
 [0.0.0.1.1.0.0.0.0.]]

用TF-IDF替代简单计数

在复杂的LSA系统中，为了重要的词占据更重的权重，原始矩阵中的计数往往会被修改。例如，一个词仅在5%的文档中应该比那些出现在90%文档中的词占据更重的权重。最常用的权重计算方法就是TF-IDF（词频-逆文档频率）。基于这种方法，我们把每个单元的数值进行修改：

TF-IDF定义如下：

• Ni,j= 某个词i出现在文档j的次数（矩阵单元中的原始值）
• N∗,j= 在文档j中所有词的个数（就是列j上所有数值的和）
• D= 文档个数（也就是矩阵的列数）
• Di= 包含词i的文档个数（也就是矩阵第i行非0列的个数）

在这个公式里，在某个文档中密集出现的词通过Ni,jN∗,j被加强，那些仅在少数文档中出现的词通过log(DDi)也被加强。

增加TF-IDF到这个LSA类中，我们需要加入以下两行代码。

      frommathimportlogfromnumpyimportasarray, sum

增加下面这个TFIDF方法到我们的LSA类中。WordsPerDoc 就是矩阵每列的和,也就是每篇文档的词语总数。DocsPerWord 利用asarray方法创建一个0、1数组（也就是大于0的数值会被归一到1），然后每一行会被加起来，从而计算出每个词出现在了多少文档中。最后，我们对每一个矩阵单元计算TFIDF公式

      defTFIDF(self):WordsPerDoc = sum(self.Mwd, axis=0)         
    DocsPerWord = sum(asarray(self.Mwd >0,'i'), axis=1)  
    rows, cols = self.Mwd.shapeforiinrange(rows):forjinrange(cols):  
            self.Mwd[i,j] = (self.Mwd[i,j] /WordsPerDoc[j]) * log(float(cols) / DocsPerWord[i])

使用奇异值分解

建立完词文档矩阵以后，用奇异值分解（SVD）分析这个矩阵。SVD非常有用的原因是，它能够找到我们矩阵的一个降维表示，他强化了其中较强的关系并且扔掉了噪音（这个算法也常被用来做图像压缩）。换句话说，它可以用尽可能少的信息尽量完善的去重建整个矩阵。为了做到这点，它会扔掉无用的噪音，强化本身较强的模式和趋势。利用SVD的技巧就是去找到用多少维度（概念）去估计这个矩阵。太少的维度会导致重要的模式被扔掉，反之维度太多会引入一些噪音。
这里SVD算法介绍的很少，使用的是python有一个简单好用的类库scipy。如下述代码所示，我们在LSA类中增加了一行代码，这行代码把矩阵分解为另外三个矩阵。矩阵U告诉我们每个词在我们的“概念”空间中的坐标，矩阵Vt告诉我们每个文档在我们的“概念”空间中的坐标，奇异值矩阵S告诉我们如何选择维度数量的线索。

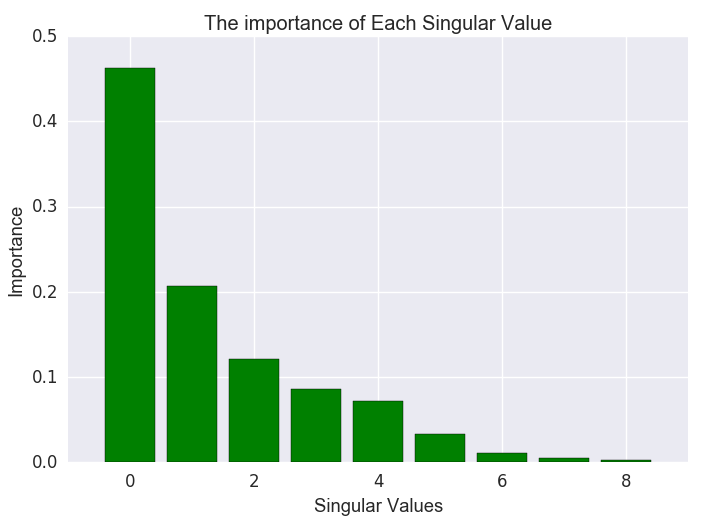
      defcalcSVD(self):self.U, self.S, self.Vt = svd(self.Mwd)

为了去选择一个合适的维度数量，我们可以做一个奇异值平方的直方图。它描绘了每个奇异值对于估算矩阵的重要度。下图是我们这个例子的直方图。（每个奇异值的平方代表了重要程度，下图应该是归一化后的结果）。

对于大规模的文档，维度选择在100到500这个范围。在我们的例子中，因为我们打算用图表来展示最后的结果，我们使用3个维度，扔掉第一个维度，用第二和第三个维度来画图（为什么扔掉第一个维度？）。

代码：

      defplotSingularValuesBar(self):y_value = (self.S*self.S)/sum(self.S*self.S)
    x_value = range(len(y_value))
    plt.bar(x_value, y_value, alpha =1, color ='g', align="center")
    plt.autoscale()
    plt.xlabel("Singular Values")
    plt.ylabel("Importance")
    plt.title("The importance of Each Singular Value")
    plt.show()

我们扔掉维度1的原因非常有意思。对于文档来说，第一个维度和文档长度相关。对于词来说，它和这个词在所有文档中出现的次数有关（为什么？）。如果我们已经对齐了矩阵（centering matrix），通过每列减去每列的平均值，那么我们将会使用维度1（为什么？）。类似的，像高尔夫分数。我们不会想要知道实际的分数，我们想要知道减去标准分之后的分数。这个分数告诉我们这个选手打到小鸟球、老鹰球（猜）等等。

我们没有对齐矩阵的原因是，对齐后稀疏矩阵会变成稠密矩阵，而这将大大增加内存和计算量。更有效的方法是并不对齐矩阵并且扔掉维度1。

下面是我们矩阵经过SVD之后3个维度的完整结果。每个词都有三个数字与其关联，一个代表了一维。上面讨论过，第一个数字趋向于和该词出现的所有次数有关，并且不如第二维和第三维更有信息量。类似的，每个标题都有三个数字与其关联，一个代表一维。同样的，我们对第一维不感兴趣，因为它趋向于和每个标题词的数量有关系。

      U:
[[-0.152835560.26603445-0.04450319]
 [-0.23746367-0.378262820.08595889]
 [-0.130265380.17428415-0.06901432]
 [-0.18440432-0.1939483-0.44568964]
 [-0.2161232-0.087272480.46011902]
 [-0.740096540.21114703-0.21075317]
 [-0.176875850.297911610.28320277]
 [-0.18440432-0.1939483-0.44568964]
 [-0.3630785-0.588541280.34119818]
 [-0.25019360.415577160.28435272]
 [-0.122936170.14317803-0.23449128]]
S:
[[3.909418040.0.]
 [0.2.609118810.]
 [0.0.1.99682784]]
Vt:
[[-0.35383506-0.22263209-0.33764656-0.25985153-0.22075733-0.49108087-0.28364968-0.28662975-0.43726389]
 [0.320937220.147724660.456349580.237765910.13580258-0.54864149-0.067743010.3070034-0.43829115]
 [0.40910955-0.140105970.15639762-0.24526283-0.222975890.50966892-0.551941650.00229626-0.33802383]]

用颜色聚类

我们可以把数字转换为颜色。例如，下图表示了文档矩阵3个维度的颜色分布。除了蓝色表示负值，红色表示正值，它包含了和矩阵同样的信息。例如，文档9在所有三个维度上正数值都较大，那么它在3个维度上都会很红。

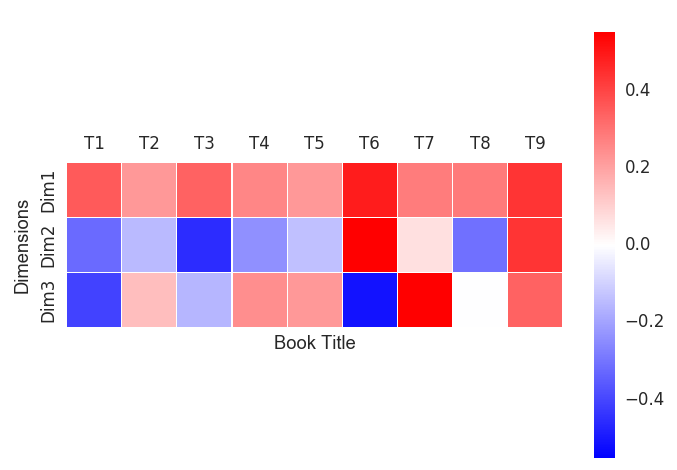
代码（这里用到了seaborn包绘制热力图）：

      defplotSingularHeatmap(self):labels = ["T1","T2","T3","T4","T5","T6","T7","T8","T9"]
    rows = ["Dim1","Dim2","Dim3"]
    self.Vtdf_norm = pd.DataFrame(self.Vt2*(-1))
    self.Vtdf_norm.columns = labels
    self.Vtdf_norm.index = rows
    sns.set(font_scale=1.2)
    ax = sns.heatmap(self.Vtdf_norm, cmap=plt.cm.bwr, linewidths=.1,square=2)
    ax.xaxis.tick_top()
    plt.xlabel("Book Title")
    plt.ylabel("Dimensions")

按值聚类

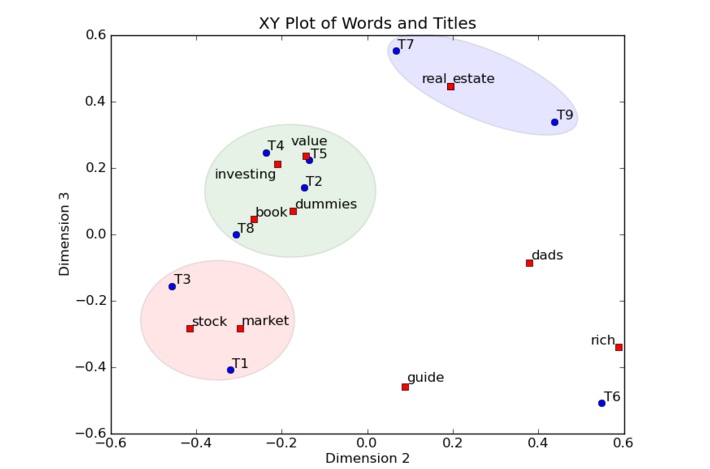
去掉维度1，让我们用xy轴坐标图来画出第二维和第三维。第二维作为X、第三维作为Y，并且把每个词和标题都画上去。比较下这个图和刚才聚类的表格会非常有意思。
在下图中，词表示为红色方形，标题表示为蓝色圆圈。例如，词“book”有坐标值(0.15, -0.27,0.04)。这里我们忽略第一维度0.15 把点画在(x = -0.27, y =0.04)。标题也是一样。

这个技术的一个有点是词和标题都在一张图上。不仅我们可以区分标题的聚类，而且我们可以把聚类中的词给这个聚类打上标签。例如左下的聚类中有标题1和标题3都是关于股票市场投资（stock market investing）的。Stock和market可以方便的定位在这个聚类中，让描述这个聚类变得容易。其它也类似。

---

LSA的优势、劣势以及应用

LSA有着许多优良的品质使得其应用广泛：

• 第一，文档和词被映射到了同一个“概念空间”。在这个空间中，我们可以把聚类文档，聚类词，最重要的是可以知道不同类型的聚类如何联系在一起的，这样我们可以通过词来寻找文档，反之亦然。
• 第二，概念空间比较原始矩阵来说维度大大减少。不仅如此，这种维度数量是刻意为之的，因为他们包含了大部分的信息和最少的噪音。这使得新产生的概念空间对于运行之后的算法非常理想，例如尝试不同的聚类算法。
• 最后LSA天生是全局算法，它从所有的文档和所有的词中找到一些东西，而这是一些局部算法不能完成的。它也能和一些更局部的算法（最近邻算法nearest neighbors）所结合发挥更大的作用。

当选择使用LSA时也有一些限制需要被考量。其中的一些是：

• LSA假设Gaussiandistribution and Frobenius norm，这些假设不一定适合所有问题。例如，文章中的词符合Poissondistribution而不是Gaussian distribution。
• LSA不能够有效解决多义性（一个词有多个意思）。它假设同样的词有同样的概念，这就解决不了例如bank这种词需要根据语境才能确定其具体含义的。
• LSA严重依赖于SVD，而SVD计算复杂度非常高并且对于新出现的文档很难去做更新。然而，近期出现了一种可以更新SVD的非常有效的算法。

不考虑这些限制，LSA被广泛应用在发现和组织搜索结果，把文章聚类，过滤作弊，语音识别，专利搜索，自动文章评价等应用之上。

---

Github地址

本文的代码已经同步到Github上， 点这里, 有兴趣的同学欢迎批评指正。

---

Ref : 参考资料

在此列出各位前辈大神的劳动成功，我都是偷他们的，谢谢。
- Latent Semantic Analysis(Tutorial)
- An Introduction to Latent Semantic Analysis
- Latent Semantic Indexing (LSI) A Fast Track Tutorial
- yihucha166博客
- zhikaizhang博客