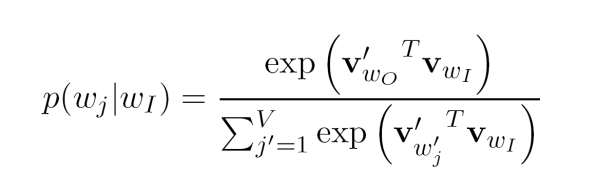本文结构：

1、Overview

2、Word Representation

3、Word2Vec

4、

5、

6、

7、

8、

 

1、Overview

Word2Vec核心包括四个组组件，Context Builder、Input Vectors、Output Vectors和Parameter Learner。Context Builder决定是了是采用CBOW模型还是Skip-Gram模型，一般采用Input Vectors作为最终的词向量输出结果，参数学习可以按照常规的反向传播算法，以及为了提升计算速度提出来的霍夫曼树softmax和负采样方法。

—

2、Word Representation

为了让计算机能够处理自然语言，需要一种表示语言的方式，通常是以词为单位。之前的做法是基于词袋的做法，用一个很长的0 1向量来表示词库中所有的词，也就是假设每个词是互相独立的，如下图所示：

这种做法带来的局限是，例如在搜索中size和capacity实际上是语义相近的，但是在one-hot编码之后，这种相似性便无法进行定义。

有很多种方法可以描述相似性，例如通过同义词词典等方法，但是通过词的表示学习（词向量）有更多优势，例如更少的参数，而且可以为下游的多任务学习建立基础。

通过词的上下文来代表词的含义是NLP最成功最有创造力的想法。对每个词定义一个向量，通过学习中心词和中心词周边的词之间的关系，确定目标函数，在大型的文档集合中的不同位置去优化（最小化）目标函数的同时不断调整各个词的词向量，经常一起出现的词应当具有相类似的词向量。

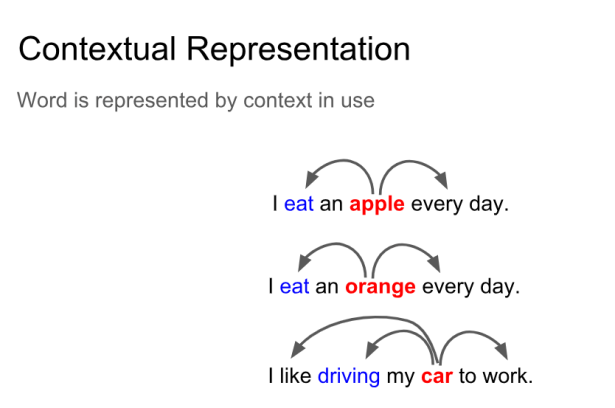
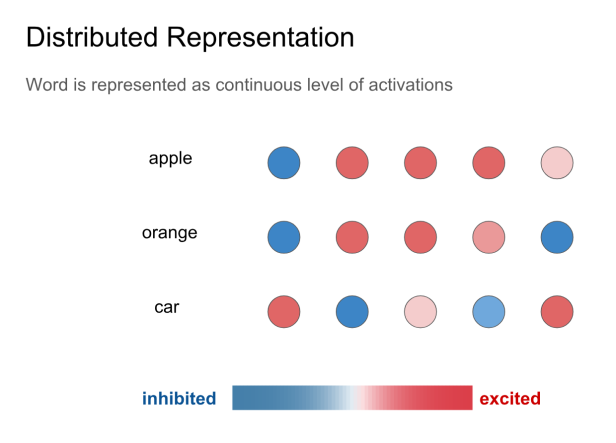
具体表现在词向量上的结果时，相似的词在某些维度上具有差不多的激活程度，就像提到桔子一词的时候，大脑内的桔子、橙子，橘子、苹果等几个词的相关神经元的激活程度差不多，如下图所示：

3、Word2Vec

Word2vec 的神经网络结构如下，总共有三层， input layer 和 output layer 一样的维度，中间的 hidden layer 比较小。 hidden layer 沒有非线性的 activation funciton ，而 output layer 的 activation function 是 sigmoid。

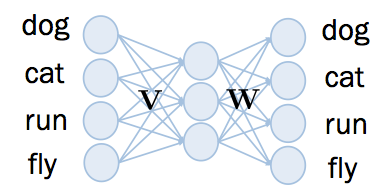
在 input layer 和 hidden layer 之间， 有 4×3 个 weight ，在此命名为V，而在 hidden layer 到 output layer 之间， 有 3×4个 weight ，在此命名为 W。其中V和W如下所示：

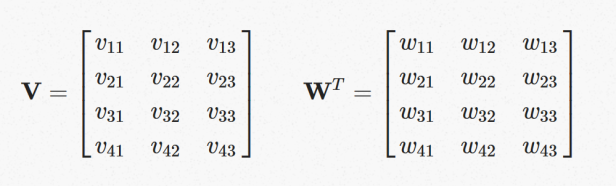
由于 input 是 one hot encoding 的向量，又因为 hidden layer 沒有 sigmoid 之类的非线性 activation function，输入到神经网络后，在 hidden layer 所取得的值，即是 V中某个横排的值，如下：

例如输入的是 dog 的 one hot encoding ，只有在第 1 个维度是 1 ，与 V 作矩阵相乘后，在 hidden layer 取得的值是 V 中的第一個横排。

因此 V中的某個横排，就是某个字的语义向量。从反方向來看，由于 output layer 也是对应到词的 one hot encoding 因此WT中的某个横排，就是某个字的语义向量。所以，一个词分別在 V 和 W中各有一個语义向量。但通常会选择 V (input vectors)中的语义向量，作为 word2vec 的输出结果。

4、理解Word2Vec的训练

初始化时随机給每个 weight 不同的数值，這些数值介于 −N∼N 之间。

某一个词语的语义，可从其上下文有哪些字來判断。因此可以用某字上下文的字來做训练，让语义向量能抓到文字的语义。若 dog 的上下文中有 run ， 令 dog 为 word2vec 的 input ， run 为 output， 则输入类神经网络后，在 run 的位置，在经过 sigmoid 之前，得到的结果是 V1 和 W3 的内积。经过了sigmoid 得到的值如下图所示：

根据上图，如果要让run的位置输出为1，则 V1 和 W3 的内积要越大越好，内积要大，就是向量角度要越小，训练过程中，会修正这两个向量的角度，如下图：

上图左方为修正之前各向量的方向，上图右方为修正之后的方向，其中深蓝色为修正后的，浅蓝色为修正前的，画在一起以便作比较。修正完后 V1 和 W3 的角度更接近。不过以上训练方法有个问题，就是训练完后 所有的向量都会位于同一条直线上，而无法分辨出每個字语义的差异 。如果要让 word2vec 学会分辨语义的差异，就需要加入反例，也就是没有出現在上下文的词。 例如dog不会fly，

所以如果要让输出結果接近 0，則 V1 和 W4 的内积要越小越好，也就是说它们之间的角度要越大越好。修正这两个向量的角度如下图：

训练完之后语义相近的词应该具有相似的词向量。

5、训练细节

对于正样本的训练，x13是 output layer 在 sigmoid 之前的值， y13 是通过 sigmoid 后的值， J 是针对这笔 positive example 所算出來的 cost function 。

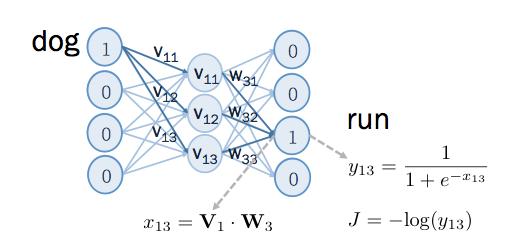
如果要更新input vector v1 和output vector w3 的值，让 J 变小，就要用 gradient descent 的方式，过程如下：

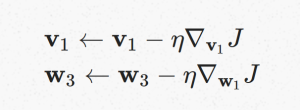
V1向量的梯度可以作为各个维度上梯度的集合：

第一项V11的梯度用chain rule拆开

拆开之后三项的值可以分别计算出来

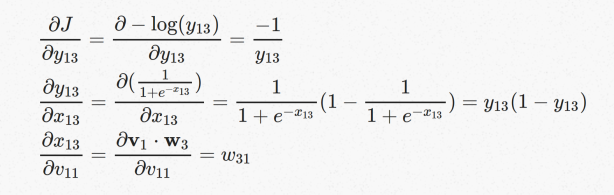
代入到V11向量的梯度，V12，V13向量的梯度也可以按照同样的方法计算出来：

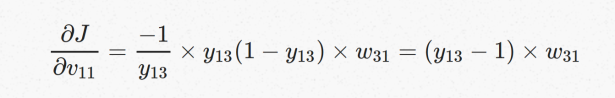
可以得到V1梯度，同理可以得到W3的梯度：

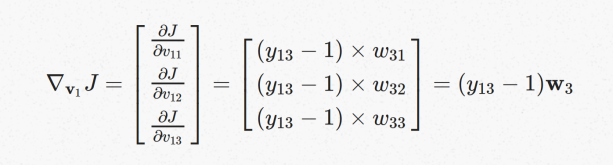
最终可以得到V1和W3的梯度下降计算公式：

其中，可以把 (y13−1) 看成是模型预测出來的和我们所想要的值差距多少。因为在 positive example 的情況下，我们希望模型输出结果 y13 为 1 。如果 y13=1 表示模型预测对了，则不需要修正 v1 和 w3 ，当 y13≠1 时才要修正 v1 和 w3 。

同理可以得到负样本训练时input vector和output vector的更新公式：

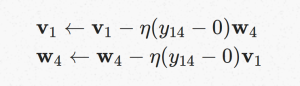
可以把 (y14−0) 看成是模型预测出來的，和我们所想要的值差距多少。因为在 negative example 的情況下，我们希望模型输出结果 y14 为 0 。如果 y13=0 表示模型预测对了，则不需要修正 v1 和 w4 ，如果 y14≠0 时才要修正 v1 和 w4。

对于如何选择输入词和上下文词有两种方式，也就是熟知的cbow模型和skip-gram模型。

6、CBOW

One-word Context

当模型在给定一个context词，只预测一个目标词的时候：

 

定义输出层的输入：

其中h隐藏层是input layer的线性输出。

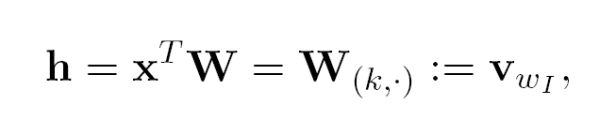
代入上面两个式子到后验分布中：

可以得到如下的条件概率：

Update equation for hidden->output weights

训练的目的是最大化上面的条件概率，也就是

E可以理解为损失函数，最终可推导出hidden->output weights的更新公式：

最终的效果是使得output vectors离input vectors更接近。

Update equation for input->hidden weights

在有了hidden->output weights的推导公式之后，可以input->hidden weights的计算公式。首先计算预测误差在隐藏层输出上的偏导：

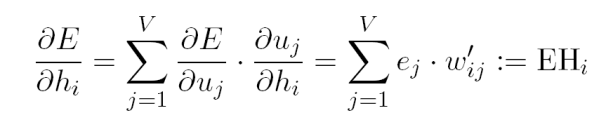
所以EH是一个N维向量，N是所有隐藏层节点Hi对应的output vectors的维度，权重是对应的预测误差。最终得到input vectors的更新方式：

可以认为上式是在更新input vector的时候，将每一个output vector的一部分加权到了input vector上。

Multi-word Context

当计算隐藏层的输出时，不同于one-word context的是，CBOW模型将会将多个input vectors取平均进行输出。

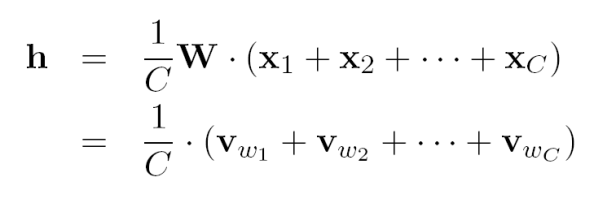目标函数是：

与one-word context不同的地方仅在于h的定义不同。output vectors的更新方式如下，值得注意的地方是对于词汇表里面的每个词都必须更新一遍：

input vectors的更新方式如下，每个context内的词都需要更新一遍：

7、Skip-Gram

Skip-Gram的模型与CBOW模型一致，同样包括输入层、投影层和输出层。对应的损失函数为：

output vectors的更新公式如下，与one-word context的更新方式一致，不同的地方在于每次更新时需要汇总C个context词的预测误差（EIj）：

input vectors的更新公式如下：

8、Optimization

对于one-word、multi-word的CBOW或者Skip-gram模型而言，input vectors的更新方式容易计算，但是要更新output vectors非常耗时。对于output vector的更新，需要计算词汇表中的每个词语，所以对于大型的语料库而言这种方法不可取，一种思路是减少每次循环中需要更新的output vectors的数量，这其中有两种方法，一种是利用hierarchical softmax，另一种是负采样。两种方法都优化了output vectors的更新，都可以理解为对原始loss函数的逼近。无论是哪种方法，都需要关注三个点： 新的目标函数，output vectors的更新方式以及反向传播时的更新input vectors前的累积误差。

9、Hierarchical Softmax

和传统的神经网络输出不同的是，Word2Vec的hierarchical softmax结构是把输出层改成了一颗哈夫曼树，其中图中的叶子节点表示词汇表中所有的|V|个词，黑色节点表示非叶子节点，都由一个向量表示（非叶子节点向量，作为算法的辅助向量），每一个叶子节点也就是每一个词语，都对应唯一的一条从root节点出发的路径。我们的目的是使的w=wO这条路径的概率最大，即P(w=wO|wI)最大，假设最后输出的条件概率是W2最大，那么只需要去更新从根结点到w2这一个叶子结点的路径上面节点的向量即可，而不需要更新所有的词的出现概率，这样大大的缩小了模型训练更新的时间[7]。

假设我们要计算W2叶子节点的概率，我们需要从根节点到叶子结点计算概率的乘积。模型替代的只是原始模型的softmax层，因此某个非叶子节点的值即隐藏层到输出层的结果仍然是output vectors，我们对这个结果进行sigmoid之后，得到节点往左子树走的概率p，1-p则为往右子树走的概率。

 

对于词典D中的任意词w，霍夫曼树中必存在一条从根节点到词w对应节点的路径pw，且这条路径是唯一的，路径pw上存在l^w-1个分支，每个分支都看作一次二分类，每一次分类就产生一个概率，每次分类由当前非叶子节点的向量和隐藏层的输出向量共同决定。

对于非叶子节点的向量，先求误差对inner向量与隐藏层向量乘积求导，最后再对inner向量求导，可得到如下更新方式：

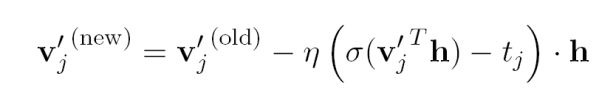
直观上理解，如果inner向量的预测与实际值很接近，那么inner向量将会移动很小距离，而当预测误差比较大时将会调整使得预测误差变小。这个公式可以用于CBOW和Skip-Gram模型，当被用于Skip-Gram模型时，这个过程需要重复C遍，因为在输出层有C个output vectors。

为了计算

将上面的公式带入原始CBOW模型中input vector的更新公式，可直接得到Hierarchical Softmax CBOW模型中input vectors的更新公式。对于Skip-Gram模型而言，在更新C个output vector的过程中，分别代入上式即可。

通过上式可以看出，经过霍夫曼树和inner向量的设计，更新output  vector的复杂度由O(V)变为O(logV)，V是词汇表的个数。

10、Negative Sampling

Negative Sampling是Noise Contrastive Estimation的一个简化版本，目的是用来提高训练速度并改善所得词向量的之类，与Hierarchical Softmax相比，Negative Sampling不再使用Huffman树，而是利用随机负采样，减少每次迭代中需要更新的output vectors的数量，能大幅度提高性能。

[9]中提出以下的目标函数能够得到很好的词向量结果：

其中Wneg指的是根据指定的分布从所有负样本中采样到的词。先对output vectors和隐藏层输出向量的乘积求偏导，得到以下公式：

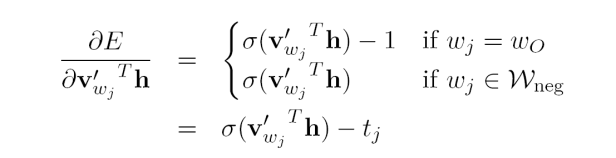
其中tj是词的label，当tj=1时代表wj是正样本吗当tj=0时代表wj是负样本。接下来对output  vector求误差的偏导，

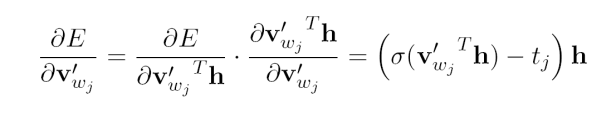
最终可以得到output vectors的更新公式：

可以看出，只需要对采样到的负样本和单个正样本进行计算，减少了复杂度。这个公式可用于CBOW和Skip-Gram模型，但用于Skip-Gram模型时每次只需过一个context词即可。为了得到input vectors的更新公式，需要将误差反向传播到hidden layer。

将得到的EH代入到CBOW和Skip-Gram模型的input vectors更新公式即可。当用在Skip-Gram模型上时，需要对

11、Dimensionality

—

—

12、参考资料

1、On the Dimensionality of Word Embedding

2、 Word2vec (Part 1 : Overview)

3、 Word2vec (Part 2 : Backward Propagation)

4、 Word Embedding Explained Slides

5、https://arxiv.org/abs/1411.2738

6、https://blog.csdn.net/google19890102/article/details/51887344

7、 word2vec（cbow+skip-gram+hierarchical softmax+Negative sampling）模型深度解析

8、 word2vec 中的数学原理详解

9、Distributed representations of words and phrases and their compositionality.

10、