天黑请闭眼,我们该怎样理性地“杀人”
对于死理性派来说,各种智力游戏是我们的拿手好戏,表演几个 计算器的小把戏 或者算出 扑克牌洗几次才能洗开 ,都不在话下。可是谁都难免有不给力的时候,如果要你用数学的方法模拟一下“天黑了请闭眼”的杀人游戏,那就算得上是个让人纠结的难题。
原因很明显,杀人游戏中有太多的运气和心理因素,死理性派的才能在各种各样的突发事件面前难以发挥。不过,一些确定的数学结论我们还是可以找到的。
这个游戏公平吗?
杀人游戏设有三个角色:杀手、平民、警察。当杀手杀掉所有警察时就可获得胜利,而如果警察和平民一起干掉坏人,好人一方(警察和平民)就会获胜。为了便于思考,我们先不设定警察这个角色,这样一来没有了指认过程,好人一方优势虽然有所降低,不过对杀手的要求也随之提高:他们要把所有的好人都杀掉才可以获胜。在这种情况下,如果10个人一起玩(不包括主持人),好人、坏人各安排多少个,才能让双方是公平的呢?
按规则,“每夜”杀手会杀死一名好人,到了“白天”大家一起投票选择选出一名嫌疑犯,并杀死TA。黑夜被杀的人一定是好人中的一员,而白天投票选出的疑犯在死亡之前身份则并不能确定。
假定所有游戏者技术相差无几,由于杀手在夜间行动,好人一方多数人难以判断到底谁是杀手谁是好人,而杀手不仅可以伪装成平民,在必要时为了不暴露身份,在投票时也会把票投给已被选择出的同伙从而保全自己。这样综合起来我们认为,每次投票导致哪个人“死亡”的概率是随机的。如果某一个时刻还剩下n个人,其中有m个坏人,n-m个好人,那么投票时死掉一个好人的概率期望值是(n-m)/n,死掉一个坏人的概率期望值则是m/n。
设置1个坏人,9个好人比较公平
根据上面的分析,死理性派就可以请出神器Mathematica,设计一个程序来模拟这个游戏:每次黑夜好人人数减1,天亮时计算机按照先前讨论得到的概率随机减少一名游戏者,当某一方的人数先减少至0时,判出胜负结束游戏。
多次运行程序,统计杀手人数和好人人数不同的时候双方赢的次数,除以游戏总次数就可以得到不同游戏人数情况下,好人获胜的概率,如下图(第一行表示杀手人数m,第一列表示总人数n)。
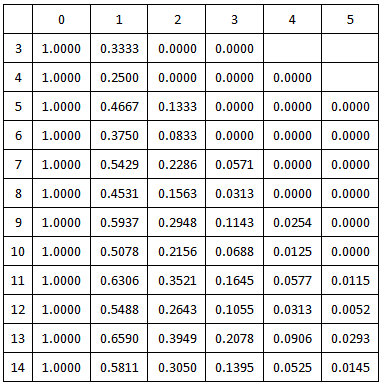
可以发现,在游戏人数为10个人且不存在警察的情况下,设置1个坏人,9个好人是比较公平的,此时双方获胜的概率大约各是50%。而一个有趣的现象是,如果坏人次数固定,好人一方并不会随着己方人数增多而使优势变大。比如杀手两个、好人五个的时候,好人一方赢的概率是22.86%;而当杀手人数不变,好人增加为八个时,好人一方赢的概率就降低为21.56%。这其实是符合实际情况的,当总人数多一些,杀手更容易混藏在人群当中。
平民和杀手的平衡公式
加利福尼亚大学伯克利分校的统计学教授Elchanan Mossel写过一篇23页的论文,内容就是杀人游戏的理论分析。文中按警察存不存在这两种情况分别讨论了平民一方的最佳策略及杀手一方的应对策略。另外他推导出当警察不存在时,杀手的数量M应该是√R级的,R是平民数,这个游戏才会平衡,由此建立出关系式M=η√R。
下图(a)为Mossel教授多次试验统计出的η和杀手胜率P的关系图,是在R=10000的情况下模拟10000次的统计图。而图(b)则显示了在η≤0.4时,模拟20000次的结果,可以发现它近乎是线性的。

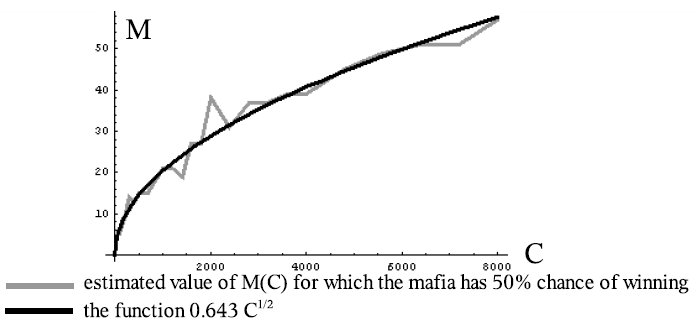
在没有警察的游戏中,规则比较简单。Mossel得出的结论是大概
M=0.643√C时(其中C是平民数)
游戏才会平衡,不过需要注意的是这都是在C值比较大的时候得出的结论,否则怎么叫作"理论分析"呢。
不过不管有多少游戏者,一旦只要设立警察这个角色,哪怕只设一个,就会彻底改变游戏的性质。杀手数量需要和平民数量保持线性关系,游戏才会平衡。
杀人游戏又叫做“警匪游戏”,在英语中被称为“mafia”,意即黑手党。关于杀人游戏的起源,一说来源于MBA的训练课程,是训练团队精神的一种心理游戏,另一说是起源于硅谷,是一群IT人士发明的一种缓解压力的游戏。这个游戏诞生于上世纪70年代,在2000年左右进入中国后迅速流行起来。杀人游戏是一个耐玩的策略游戏,不过很早以前许多城市街边的路摊上就已经也遍布各类策略游戏了,你至少见过如下这个,不妨试一试,想想破解之道吧。

参考资料:
1、A mathematical model of the Mafia game, Piotr Migdal
2、月黑杀人夜——游戏中的数学,2001年《科学中国人》杂志
3、Mafia : A Theoretical Study Of Players and Coalitions in a Partial Information Environment