五角星中的黄金分割点

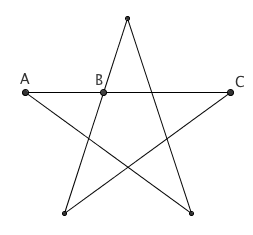
在正五角星中，每条线中间的点都是这条线段的黄金分割点。例如，上图中，点 B 就是线段 AC 的黄金分割点。

三根木杆搭出黄金分割点

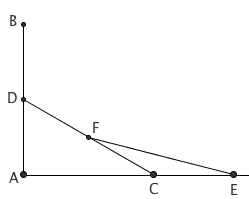
在水平地面的 A 点处竖立一根木杆 AB。把一根相同长度的木杆 CD 斜靠在 AB 上，其中 D 点正好是 AB 的中点。再把一根相同长度的木杆 EF 斜靠在 CD 上，其中 F 点正好是 CD 的中点。则点 C 是线段 AE 的黄金分割点。

用正多边形构造黄金分割点

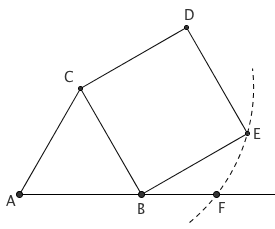
作等边三角形 ABC。以 BC 为边向外作正方形 BCDE。以 C 为圆心，CE 为半径画弧，与 AB 所在直线交于点 F。则 B 是线段 AF 的黄金分割点。

3:4:5 直角三角形中的黄金分割点

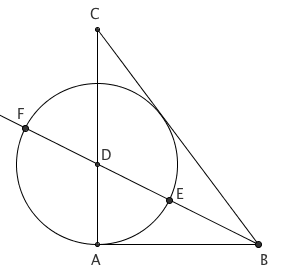
如果一个三角形的三边长分别为 3、4、5，由勾股定理，这个三角形是一个直角三角形。在所有边长均为整数的直角三角形中，这是最小的直角三角形。这一性质让它成为了最经典的直角三角形之一。

想不到，利用这个经典的直角三角形，也能快速构造出黄金分割来。作一个 3:4:5 的直角三角形 ABC。作角 B 的角平分线，与 AC 交于点 D。以 D 为圆心， DA 为半径作圆，与角平分线分别交于 E、F。则 E 是线段 BF 的黄金分割点。

等边三角形与外接圆构成的黄金分割点

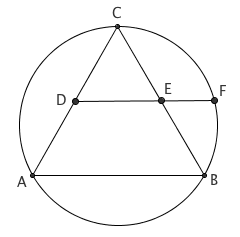
作等边三角形 ABC。D、E 分别是 AC、BC 的中点。DE 的延长线与整个三角形的外接圆交于点 F。则 E 是线段 DF 的黄金分割点。

三个圆确定出来的黄金分割点

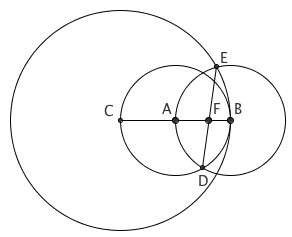
以 AB 为半径，分别以 A、B 为圆心作圆。BA 的延长线与圆 A 交于点 C。以 C 为圆心，CB 为半径作圆。连接图中所示的 D、E 两点，它与 AB 交于点 F 。则 F 是 AB 的黄金分割点。

三个相交等圆中的黄金分割点

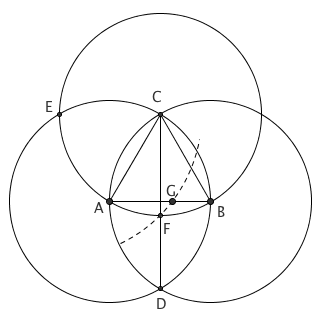
作等边三角形 ABC。以它的边长为半径，分别以 A、B、C 为顶点作三个等圆，其中 ⊙A、⊙B 两圆交于点 D， ⊙A、⊙C 两圆交于点 E。CD 与 ⊙C 交于点 F。以 E 为圆心，EF 为半径作弧，与 AB 交于点 G。则 G 是 AB 的黄金分割点。

三个相切等圆中的黄金分割点

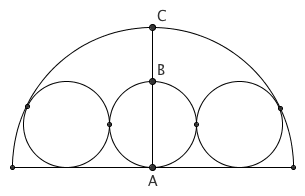
三个等圆依次相切，它们又都紧紧地包含在一个半圆中。则半圆的半径与小圆的直径是黄金分割比，也就是说图中 B 是线段 AC 的黄金分割点。

单规作出黄金分割点

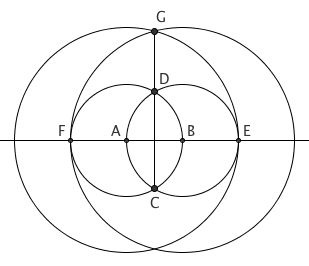
以 AB 为半径，分别以 A、B 为圆心作圆，两圆相交于 C、D 两点，同时这两个圆分别与直线 AB 交于 E、F 两点。分别以 A、B 为圆心，AE、BF 为半径作圆，两圆相交于点 G。由对称性，C、D、G 三点显然共线。则 D 是线段 CG 的黄金分割点。

注意，即使没有 AB 这条线，我们也能通过作出以 C 为圆心 CD 为半径的圆，确定出 E、F 两点来。因此，我们就有了一种不用直尺，只用圆规就能作出黄金分割的方法来。

你最喜欢哪种构造？