以函数图象解析游戏机制中的数学原理

作者：Tyler Sigman

无论是跟策划团队讨论游戏功能，还是和程序师沟通执行代码，缺乏合适的术语可能会造成信息错乱。

但凡技术背景深厚的程序员，大抵都学过数年严格的专业课程。所以，如果设计师试图解释一个他所设想的机制，但却用错了术语，那么他要传达的信息可能就丢失了。

要理解大多数的游戏机制，有一定的数学基础就行了。所以一般来说，用已经公认的数学术语描术游戏机制，合情合理。

本文的第一部分主要是通过图象直观地展示游戏机制，并解释相应的术语含义。第二部分将更结合几个游戏案例，详尽地探讨第一部分所示的游戏机制。

图表中的直观值

一幅图像胜过千言万语。

我曾想到更机敏，更简洁明了地解释游戏机制的值，但我怕机智过人的网民会当场攻击我，所以算了吧。

如果说用图像有什么缺陷的话，就是仍然需要描述。所以读者们仍然要读完这整篇文章。首先，我们先了解一些基本的术语，然后再深入其含义。

术语1：函数

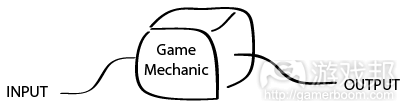
从数学的角度来说，游戏机制充其量就是函数。函数就是一个数学“黑盒”。把某个已知的输入值丢进这口黑盒（游戏机制）里，一个输出信息就出来了。

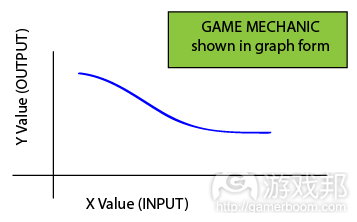
从图像的角度来说，函数可以用一个X-Y座标图加一条直线或曲线来表示。

术语2：函数值域

游戏机制的值域是函数（机制）有效的取值范围。在图像里，值域由X轴表示（横坐标）。

比如，“命中率作为来复枪技能的函数”。这此，值域就是来复枪的技能范围——如1~10或1~100等（根据游戏系统取值）。

又比如，“加速度作为排档的函数”。此时，排档的范围就是值域——如1~5。

术语3：斜率

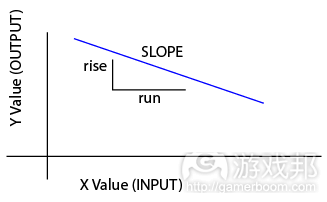
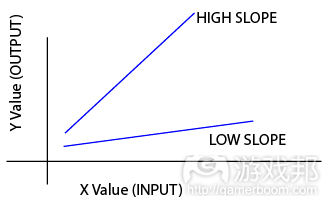
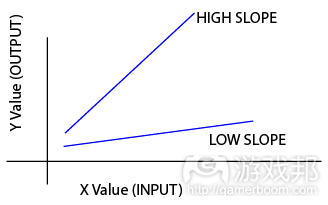
斜率是指函数图像上的直线或曲线的角度。斜率的学术性说法是“上升”，也就是根据给定的X值，改变Y值。负斜率呈下降趋势；正斜率呈上升趋势。

根据概念，高斜率是指快速改变的机制，而低斜率是指缓慢改变的机制。

无论该机制（函数）是线性还是非线性，你总是可能定义局部斜率。在线性函数中，斜率始终不变，而在非线性函数中，斜率总是在改变。

术语4：线性

游戏机制（函数）的描述性特征之一，是线性还是非线性。从名称就可以看出来，“线性”就是“像线一样”。数学上的说法是，机制的斜率是恒量。实际上看，这意味着函数（机制）以一定的率，呈递增或递减。

线性机制的例子：

纯转向：方向盘的方位与转向率呈线性相关。

纯武器攻击作为充能时间的函数：如果你充能2秒后进攻，那么伤害就是充能1秒后释放伤害的2倍。

纯命中率作为武器技能的函数：如果武器的技能指数25，那么玩家需要进攻2次才能达到指术为50的武器的命中率。

纯经验奖励作为怪物等级的函数：打改一只等级4的怪物给的经验是打等级2的怪物的2倍。

术语5：非线性

如果机制不是线性的，那么它就是非线性的（好吧，我这是多此一言）。

已经有了那么多线性机制了，应该有一个非线性的。好吧，可能不会非常多，但我想说的是，非线性机制极其普遍。有时候你需要使用非线性关系，因为线性机制不能准确地模拟或完成你的设计意图。

非线性游戏机制的例子：

几乎所有的RPG角色升级和经验积累：从等级1升到等级2可能可需要1000的经验值，但从等级20爬到21，可能要1000000。

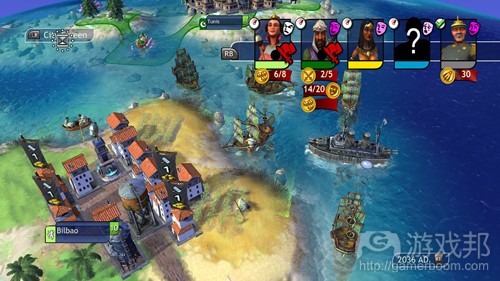
《文明》中的人口增长：500年之后的文明，人口数可能是500年前的5倍……除非你的文明正在走向衰亡。

赛车的加速度作为“秒”的函数：真实小车的加速度在低档时更高，高档时更低。小车的速度可能在6秒内从0加到60英里/时，但你不能指望在接下来的6秒里再把速度上提60英里/时。

《几何战争》中积分作为游戏时间的函数：如果你可以坚持20分钟，你的得分肯定比坚持10分钟的人高不止2倍。

我们对非线性机制非常熟悉，从通俗对话中可见：

“收益递减法则”

“几何膨胀”

非线性机制的类型

线性机制的差别只是斜率，而非线性机制的类型就非常多了。 所以有必要把非线性机制划分为：

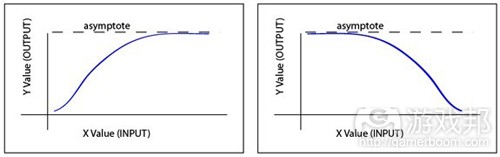
渐近某值：这类机到达某个值点（Y上的值）后就制趋平。在这个值点后，无论X有多大，Y值的改变都非常小（或不重要）。也就是，到达某个值点以后，斜率呈0。

例子：基于武器技能的命中率：你可以设计一个战斗系统，随着玩家武器技能增加，命中率也增加，但达到某个值后，无论玩家的武器技能如何增加，最终的命中效果已“达到极限”。

无限接近：当X值增加或减少时，Y值不断接近无限。

例子：人口增长（几何膨胀）。从技术上说，有些限度最终会显示出来（如地球的人口承载能力？），但在达到那个限度以前，人口会跟据无穷大函数关系增长。

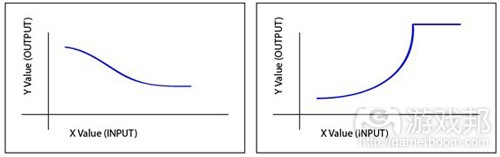
非渐近：非线性函数永远不会“趋平”或“接近无限”。

分段线性

分段函数总体上可以当作是线性函数，也就是由两个或更多斜率不同的分部组成的线性函数。

比如小车的变速器机制就是一个分段函数的例子。你可以模拟一个加速器和转矩作为速度的函数。每一个排档都有两个不同的值。结果函数是由数段不同的线性函数组成的，每段都有各自的斜率。

线性和非线性共存

如果你喜欢巧克力，同时也喜欢香草，为什么不把二者混合起来呢？你不应该在这上面纠结。当设计游戏机制时，你完全可以一部分值域是线性的，另一部分是非线性的。

然而，你应该避开这么复杂的东西，除非你有充分的理由。

如何选择合适的机制：线性或非线性或组合？

设计游戏是科学和艺术相结合的过程。在这个过程中，你得在简单和准确性之间作权衡。所有因素都要纳入设计考虑：你需要多高的仿真精度？你要模拟的机制的知名度？调整、再调整以及平衡的难度是多少？其他成员对机制的了解情况怎么样？终端用户（玩家）能不能理解机制？……

我的设计法则41A：在实现设计意图的前提下选择最简单的机制。

在AI编写中，这近乎信手拈来的公理。记住你的目标不是制作最逼真/高级/创新的系统，而是以最少的代价实现设计意图。换句话说，你的游戏机制只需要达到你的目标就好了。

这不是说总是选择简单的——有时候只有复杂的系统才能表现设计意图。但总是选择可行又简单的方式，因为这会便利接下来的调整、修改、反复和理解。

为了简化执行：

1、线性机制

2、非线性机制，单一的方程式（如 y = x2）

3、分段线性机制

4、非线性机制，多重方程式；线性/非线性组合机制

但是，不要混淆了执行复杂度和玩家实际看到或体验到的复杂度！

我的设计法则41B：执行机制的复杂度不总是与玩家理解上的机制复杂度相等。

非线性机制的执行难度总是比线性机制的大，但并非总是难以理解！正如我前面所说的，大家对“递减收益”这种概念都非常熟悉嘛。原因是我们在日常生活中每天都会遇到大量不同的机制，其中有不少是非线性的。

小车的速度从0~60之间的加速度始终不同；兔子数量呈指数增长；或你的金融投资可能在某个关键时刻变成任何数字，这些现象都不难理解。我们每天都绕着机制转，虽然我们并没有意识到这点。

如果你正在制作模型或动作游戏，学习真实的机制将大有裨益。

生活中的线性机制

移动速度和距离：如果你以120英里/时的速度呈直线运动，你的运动距离将是60英里/时的2倍。当然，这很明显，但这对你来说是线性机制！

动能作为质量的函数：若一飞行物，其称量为2磅，移动速度为50英尺/秒，那么它的动能是相同移动速度但称量为4磅的飞行物的一半。

对流层的温度：从地球表面上升到对流程的过程中，气温以稳定率（温度垂直递减梯度）降低。

生活中的非线性机制：

美国联邦税收：多亏了美国税收（游戏邦注：包括纳税等级、逐渐淘汰的扣除额等等等）牵涉到的因素错综复杂，那些挣10万的人不必比那些挣5万的人多交一倍的税了。但实际上在你的纳税申报单中，你最近一次为挣得10美元而交的税比第一次挣得10美元交的还多（假设你已达到第二级边际税收等级）。税收等级系统的核心是分段线性函数。

举重训练：你每小时中所做的力量训练并没有获得相同的力量。有时候你快，有时候保持平衡。（非线性增长）

人口增长：如果你以10年为一个时段看待人类历史，你会发现，新出生的人口数量呈非线性增长。（非线性增长）

复合利息：如果你在20岁时投资1000美元，利息为5%，到了60岁，你的总值就是7040美元。如果在相同情况下，你到了40岁才投资，那么20年后你只能得到2653美元（前者的37.7%）。如果利息复合是线性机制，那么，20年的投资价值就是40年的投资的一半。（非线性增长）

薪水作为经验年数的函数（我承认我总想调查一下游戏开发人的薪水情况）：工作了15年的人的薪水不一定是5年工作经验的人的3倍。（非线性减少）

引力：两物体之间的吸引力随着距离呈非线性减少。如果你的体重是200磅，在水平面（与地心的距离大约是4000英里），当你所在位置的高度增加一倍后，你的体重会比原体重的一半还少。

动能作为速度的函数：一个5磅的物品以100英里/时的速度运动，此时的动能是它在50英里/时的4倍。（非线性增长）

数据的正常分布（即“钟形”分布）前10%段的值比中间10%段的值更稀疏得多。

游戏机制1：经典典型RPG中的等级

简要描述：人物升级，关键属性和技能也随之提升。升级需要一定量的经验点（通过完成各种种样的任务获得）。后面的等级所需的经验点比前面的等级的经验点多。

剖析

说到经验点系统，有两个主要的分析方法。上图就是方法1的图表，这是最常用的一种，即到达下一级所需的经验点呈非线性增加。如，升到2级所需的经验点是1000，但升到20级，需要的经验点就接近200000了！

几乎所有RPG都采用这种系统，如《龙与地下城》。这个系统的优势在于，对越高级的怪物奖励的经验点越多，所以玩家很容易在不同的怪物之间作比较。另外，玩家会获得更多的奖励时，会产生一种成就感。

另一种经验点/升级系统是保持恒定的升级斜率（如每升一级需要1000经验点），但根据玩家的等级调整打怪所获得的经验点。例如，1级的角色打怪一只小怪可得50经验点，但10级的角色打相同的小怪只能获得5经验点。

游戏机制2：《帝国时代：王朝DS》的采金量

简要描述：在这款游戏中，玩家可以从每堆金矿中开采到200的金。如果你有3堆矿，那么你能得到的金量就是600（不计技术升级的增益）。

剖析

这种收入机制完全是线性的。就相当于，农田越多，获得的食物也成比例地增加。

你认为设计师为什么要选择线性机制呢？

我严重地怀疑：这是因为线性机制是模拟合适的经济活动的最简单方式。也就是，没有必要搞一套复杂的非线性机制——两堆金的产量比一堆金的产量多一倍不是很理想嘛，也很符合逻辑啊！既然游戏的核心是战略和策略，那么没有什么必要把经济活动弄得太复杂。

（设计师本可以在采金方面再加上效率机制……但为什么要自找麻烦？这款游戏根本没必要这么复杂。）

其实我说的就是事实，因为我本人正是这个系统的设计师。

游戏机制3：《车票之旅》的路线积分点

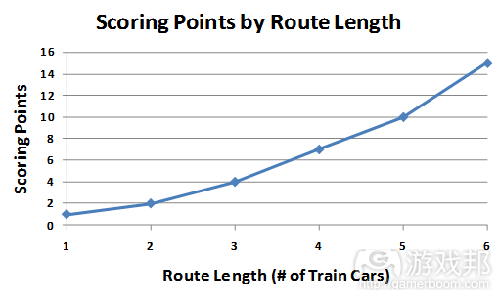
简要描述：在这款游戏中，玩家通过获得两个不同城镇之间的火车线路得到积分点。而拿下火车线路需要足够的相应的火车颜色卡片来适应线路的长度（游戏邦注：例如，四张红色火车卡片可以得到长度为四的红色线路）。积分点与路线长度之间是非线性关系——长度为六的线路奖励15点，但长度为三的线路只给4点。

剖析

拿下长度为六的路张得到的胜利点是长度为三的2倍。你认为设计师为什么选择了非线性机制？

虽然许多机制是艺术的选择，但我认为在这里，采用非线性机制完全是出于真实有效的考虑。这是因为如果机制是线性的，那么这款游戏的乐趣就会削弱了。

如果拿下长度为六的线路的价值是长度为三的2倍，或者长度为四的是长度为二的2倍，那么单纯地为了接通两个目的地，玩家就没有动力去争取更长的线路。

但现在线路长度与胜利点呈非线性关系，玩家就有了额外的动机：如果你可以节省给定色卡，同是得到长路线，那么回报就比较可观了。玩家有理由选择性地保留自己的火车卡，而不是单纯地把它们浪费在看似有前途的线路上。毕竟，这是一款策略游戏。

（游戏邦注：长度为二的线路价值确实只是长度为一的2倍。然而，拿下长度为二的线路显然比拿下长度为一的更难，所以此时的非线性机制就没必要了。）

游戏机制4：《星战前夜 》的星际飞船保险单

这年头谁还谈保险啊？但这只是个游戏，所以还是值得一提，因为这里的破坏机制与战斗的破坏机制没有太大的差别。

简要描述：在《星战前夜 》中，玩家可以为自己的星际飞船购买替换险。如果飞船以正当的方式损坏（非自残），保险公司就会根据飞船的价值和玩家所购买的保险级别来支付星际Kredits (ISK)。

剖析

顺便一提，免费险的保险范围是飞船价值的40%。

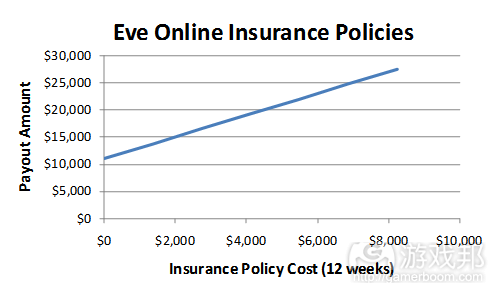
我们用曲线图来表示这些数值吧。在此，值域（X值）是购买保险的成本，偿还金是Y值。游戏机制或功能就是隐藏在这些图像之后的保险购买成本和偿还值。

剖析

如你所见，该机制是线性的。保险成本为0时偿还的值相当于飞船的40%。保险成本为8250偿还了几乎相当于飞船99%的价值。

你认为开发者为什么选择线性机制？与非线性的保险机制相比，线性机制的优势和劣势何在？

飞船保险单的有效期是12周。有效期又是如何影响保险成本的结构？

结语

线性和非线性是核心的游戏系统设计元素。从制定计划到物品掉落，所有活动都受到曲线选择的巨大影响。

如果你在游戏设计中有所心得体会，不妨提出来共享！

游戏邦注：原文发表于2009年7月29日，所涉数据及内容以当时为准。（本文为游戏邦/gamerboom.com编译，如需转载请联系：游戏邦）

Anatomy of a Game Mechanic

by Tyler Sigman

[Game design veteran Sigman presents a detailed look at how game mechanics can be represented visually -- and what we can learn about how to make great video games thanks to such alluring graphs.]

Whether discussing game features amongst the design team or communicating them to programmers, lack of proper terminology can obfuscate messages. (Just like how using the word “obfuscate” can obfuscate messages.)

Game Advertising Online

Coders have technical backgrounds and most went through rigorous college-level math classes. As a result, if a designer is trying to explain a desired mechanic but using the wrong terms, the message content can be lost.

The foundations of math provide a convenient basis for understanding most game mechanics, so it generally makes sense to describe game mechanics in established mathematical nomenclature.

The first part of this article is a short primer on visual representation of game mechanics and some proper terms to describe those representations. The second half discusses a few selected game mechanics in more detail for illustrative purposes.
Visual Value in a Graph

A picture’s worth a thousand words.

No, seriously. I was trying to think of a wittier, more concise way to explain the value of talking about game mechanics visually, but societal wisdom beat me there.

The hitch about using visuals is that you still need a way to describe them. So you kinda still need those thousand words after all. So let’s dive in with some foundation items, and then we’ll get to the fun stuff.

Term: Function

Mathematically, a game mechanic is usually just a function. A function is a mathematical “black box”. Given a certain input, the black box (game mechanic) creates an output.

Game Mechanics are Functions (Black Boxes)

Graphically, a function is represented by a line or curve in an X-Y plot:

A Function

Term: Domain

Function Domain

A game mechanic’s domain is the range of values over which the mechanic is active. Graphically, this is represented by the X-axis (“abscissa”).

Take an example game mechanic: “shooting accuracy as a function of RIFLE skill.” The domain is the RIFLE skill range — say 1-10 or 1-100 or whatever your game system is.

Another example is the mechanic “acceleration as a function of transmission gear.” In this case, the domain is the range of gears in the vehicle — say 1 through 5.

Term: Slope

Slope

Slope refers to the angle of the line or curve of a graphed mechanic. Technically, slope is described as “rise over run”, which is just the change in Y value for a given change in X value. Negative slope means downward trending; positive slope is upward trending.

Conceptually, a high slope means a fast-changing mechanic, whereas a low slope is a slowly-changing mechanic.

High and Low Slope

Whether the mechanic is linear or non-linear (see later), you can always still define a local slope. In the case of a linear mechanic, the slope is constant; for non-linear mechanics, the slope changes all over the place.

Term: Linear

One of the most useful descriptive characteristics of a game mechanic (a.k.a. function) is whether it is linear or non-linear. Linear is pretty much like it sounds — “like a line”. Mathematically, this means the slope of the mechanic is constant. Practically, this means that the mechanic steadily increases or steadily decreases at a given rate.

Linear Mechanics/Functions

Examples of Linear Mechanics:

* Simple steering: position of the steering wheel corresponds linearly to turn rate

* Simple weapon damage as a function of charge-up time: if you charge up for 2.0 seconds, the damage is twice what it is if you charged up for 1.0 seconds

* Simple To-Hit Chance as a function of weapon skill: having a Weapon Skill of 50 gives the player two times the chance to hit as a Weapon Skill of 25.

* Simple XP Rewards as a Function of Monster Level: defeating a level 4 monster gives twice as much experience as defeating a level 2 monster

Term: Non-Linear

If a mechanic is not linear, then it is non-linear. I know — big surprise.

For every linear mechanic out there, there’s probably a non-linear one. Well, maybe not that many, but the point is that non-linear mechanics are extremely common. Sometimes you need to use a non-linear relationship because a linear mechanic just doesn’t accurately simulate or accomplish your design intent.

Non-Linear Mechanics/Functions

Examples of Non-Linear Game Mechanics:

* Almost every RPG character level advancement XP table ever created (you can thank the late Gary Gygax or Dave Arneson for that): it might take only 1,000 XP to climb from level 1 to 2, but it could take 1,000,000 XP to climb from level 20 to 21.

* Population growth in Civilization: your Year 500 Civ will typically have more than five times the population of your Year 100 Civ… unless you’re on your way to extinction.

* Car acceleration as a function of “seconds from the line” in a driving game: real cars have higher acceleration in lower gears and lower acceleration in higher gears. You may travel 0-60 in 6 seconds but you can’t expect to gain another 60 MPH in the next 6 seconds.

* Score as a function of time played in Geometry Wars: if you can last 20 minutes, you’ll surely have far more than twice the score of someone who played for 10 minutes.

Non-linear mechanics are very familiar to us and more colloquial ways of describing them exist. For example:

* “the law of diminishing returns”

* “geometric expansion”

Types of Non-Linear Mechanics

While linear mechanics differ only by their slopes, there are many different types of non-linear mechanics. It is often necessary to subclassify them further as one of the following:

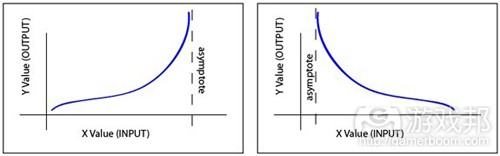
* Asymptotic to a value: these mechanics tend to “flatten out” as they approach a certain result (y value). After a point, huge changes in X result in very small (insignificant) changes in Y. In other words, slope approaches zero after a certain point.

o Example Mechanic: to hit chance based upon weapon skill: you might design a combat system that eventually “tops out” the player’s chance to hit as his weapon skill increases. After a point, further increases in weapon skill have little effect.

Asymptotic to a Value

* Asymptotic to infinity: these mechanics tend to approach infinity (Y) as X increase or decreases.

o Example: Population Growth (geometric expansion). Technically, some limit will eventually exert itself (e.g. capacity of the planet?), but until that limit, the mechanic may follow an Asymptotic to Infinity relationship.

Asymptotic to Infinity

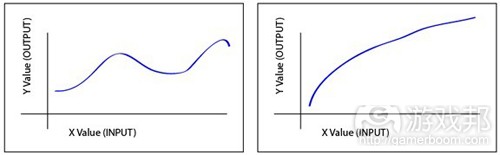
* Non-asymptotic: the non-linear mechanic doesn’t ever “level off” and isn’t asymptotic to infinity.

Non-Asymptotic

Segmented Linear

A segmented linear mechanic is technically non-linear overall, but you can think of it more as just a linear mechanic that is made up of two or more sections with different slopes.

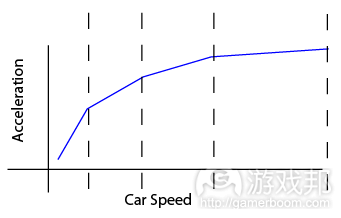
An example of a segmented linear mechanic would be a really simple car transmission mechanic where you are modeling acceleration and torque as a function of speed. Each gear would have different values. The resulting graph would be made up of several different linear “gear bands”, each with a different slope.

Segmented Linear Mechanic: Notice the Distinct Linear Sections

Segmented Linear mechanics are relatively easy to create and often are a great way of simulating a complex non-linear mechanic. If the assumption that the mechanic is linear between various key points is good enough, then it can be a good way to go and they are very tunable.

Linear and Non-Linear Living Together

If you like chocolate and you like vanilla, why not combine them together and have both? In and Out Burger doesn’t fight you on that, so you shouldn’t fight yourself. When designing a game mechanic, there’s no reason why you can’t have some portions of the domain be linear and some non-linear.

However, you should probably avoid such complexity unless you have a really good reason. (See next page.)

Notes on How to Choose the Right Mechanic: Linear or Non-Linear or Combined?

Designing game mechanics is part science, part artistry. Typically you have to make trade-offs between simplicity and accuracy. All sorts of factors should be weighed in a design decision: How accurate of a simulation do you want? How well known is the mechanic you are trying to model? How simple will it be to tune, retune, and balance? Will other team members understand it enough to work on it? Will the end-user (player) understand it? And so on.

Sigman Design Rule 41a: Choose the simplest mechanic that satisfies your design goal.

Game Advertising Online

KISS and all that. This is similar to a very handy axiom in AI Programming. Remember that your goal is not to make the most eloquent/advanced/innovative SYSTEM, but rather to accomplish a DESIGN GOAL with the minimum amount of required work. In other words, your game mechanic only needs to be as clever as it needs to be. A bit Zen-like, but true.

This isn’t to say always go simple — sometimes a design goal can only be achieved with a complex system. But always go as simple as you can get away with, because that will facilitate easier tuning, adjustment, iteration, and understanding.

In order of simplicity of implementation:

1. Linear mechanic

2. Non-linear mechanic defined by a single equation (e.g. y = x2)

3. Segmented Linear mechanic

4. Non-linear mechanic defined by multiple equations and/or combined linear/non-linear mechanic

However, don’t confuse implementation complexity with the complexity that the player sees or experiences!

Sigman Design Rule 41b: Complexity of implementing a mechanic does not always equal the player’s complexity of understanding that mechanic.

Non-linear mechanics are usually more complex to implement than linear mechanics, but they aren’t typically hard to understand! Like I mentioned earlier, concepts like “diminishing returns” are intuitively familiar to many people. The reason is that we encounter tons of different mechanics in everyday life, and many of them are non-linear.

It is not hard to understand that a car’s acceleration varies over its 0-60 run (as gears are changed), or that bunnies multiply exponentially, or that your financial investments can behave any number of ways in between key time periods. People observe mechanics all around them every day, even if they aren’t thinking about it.

If you are making a simulation or an arcade action game, studying real-life mechanics is hugely important to game design.

A Few Linear Mechanics in Life

* Travel speed and distance: if you travel at 120mph in a straight line, you cover twice as much distance per hour as you do traveling 60mph in a straight line. Yes that sounds obvious, but that’s a linear mechanic for you!

* Kinetic energy as a function of mass: a flying object moving at 50 feet per second and weighing 2 lbs. has exactly ½ of the kinetic energy of a flying object moving at the same speed but weighing 4 lbs.

* Temperature in the troposphere: temperature tends to decrease at a steady rate (“lapse rate”) from the surface on up to the tropopause.

A Few Non-Linear Mechanics in Life:

* US Federal Taxes: thanks to the myriad of factors involved in US taxes (including tax brackets, phased out deductions, and a million other things), someone who earns 100k isn’t guaranteed to pay twice as much taxes as someone who earns 50k. But even within your own tax return, you pay more taxes for the last $10 you earn than the first $10 you earn (assuming you make enough to hit the second marginal tax bracket). The core tax bracket system is segmented linear.

* Weight training: for every hour you do strength training, you don’t gain the same amount of strength. Sometimes you have rapid gains, and sometimes you plateau for a time. (non-linear decreasing)

* Population growth: if you look at human history in 10 year segments, the amount of new people born each decade increases non-linearly. (non-linear increasing)

* Compounding Interest: if you invest $1,000 in a 5% earning money-market account at age 20, it will be worth $7,040 at age 60. If you had invested the same $1,000 at age 40, it would only be worth $2653 at age 60 (37.7% of the former). If interest compounding was a linear mechanic, you would have expected a 20 year investment to be worth exactly 50% of a 40 year investment. (non-linear increasing)

* Salary as a function of years of experience (Ok, the Game Developer Salary Survey is always on my mind): someone with 15 years of experience doesn’t typically make 3 times what a person with 5 years of experience makes. (non-linear decreasing)

* Gravity: the attraction of two bodies decreases non-linearly with distance. If you weigh 200 lbs. at Sea Level (~4,000 miles distance from the center of the Earth), you will actually weigh far less than half of that at an altitude of twice that.

* Kinetic energy as a function of speed: a five-pound object moving at 50 mph has four times as much kinetic energy when moving at 100 mph (non-linear increasing)

* A normal (aka “bell shaped”) distribution of data (see my Statistics article <LINK>): values in the upper 10% band are far more rare than those in the middle 10% band.

Ok, enough about real life. Let’s do a couple quick case studies of actual game mechanics.
Game Mechanic #1: Leveling Tables in Typical Role-Playing Games

Quick Description: Characters gain “levels”, which correspond to predefined improvements in key attributes and skills. It takes a certain amount of Experience Points (earned through completion of various tasks) to gain levels. Later levels cost vastly more Experience Points to advance than early levels.
Graph It!

Typical Experience Point / Level Chart

Dissect It!

When it comes to an experience point system, there are two main ways of skinning the cat. Method 1, which is by far the most popular, uses an experience point curve like that shown above — experience to reach the next level increases non-linearly. Only 1,000 may be required to achieve level 2, but you’ll need a total of nearly 200,000 to reach level 20.

This system was used in the grandpappy of all RPGs, Dungeons and Dragons. The advantage of this system is that bigger monsters award the player larger XP numbers, so it is easy to compare monsters on an apples to apples basis. Also, the players feel a sense of accomplishment in gaining the larger rewards.

For completeness’ sake, the other common system for XP/Levels involves keeping a constant level ramp (say 1,000 XP per level) but adjusting XP awards for monsters to be relative to the players. For example, defeating a kobold with a level 1 character may yield 50 XP, but defeating the same kobold with a level 10 character might only award 5 XP.

Game Mechanic #2: Gold Income in Age of Empires: the Age of Kings DS

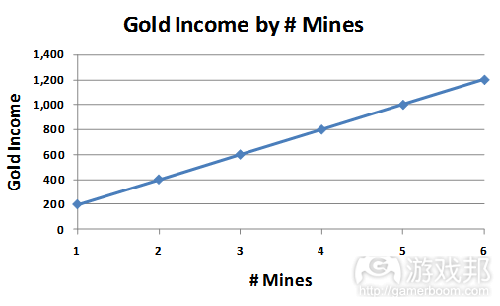
Quick Description: In this game, the player earns 200 gold per turn for each mine. If you have 3 mines, you earn exactly 3 times the income of 1 mine (3 x 200 = 600 gold), not counting tech bonuses.

Graph It!

Gold Income as a Function of # Mines in Age of Empires: the Age of Kings DS

Dissect It!

This income mechanic is totally linear. More farms gives a directly-proportional increased food income.

Why do you think the designers chose a linear mechanic in this case?

I have a strong suspicion* that this was a simple case of it being the simplest way to get the desired economic simulation. That is, there was no strong reasoning for having a non-linear mechanic — it’s logical and expected that two mines produce twice as much as one mine. Given that the focus of the game is on core strategy and tactics, there wasn’t any compelling justification to model second-order effects of a complex economy.

(The designers could have included an efficiency mechanic that simulates more or less efficiency as the combined network of mines increases… but why bother for this game about skirmishes? It would just be adding complexity where it isn’t needed.)

*My suspicion is actually fact, since I designed that particular system

Game Mechanic #3: Victory Points for Routes in Ticket to Ride

Quick Description: In this game, you earn victory points by claiming train routes between different towns. Train routes are claimed by playing enough matching train color cards to fit the route length (e.g. four red train cards to claim a length four red route). Victory Point awards are non-linear for route length — a length six route awards 15 points whereas a length three route gives only four points.

Graph It!

Scoring Points for Different Route Lengths in Ticket to Ride

Dissect It!

Once again, we have a non-linear mechanic breathing down our necks. Claiming a length six route is more than twice as valuable as claiming a length three route. Why do you think the designer chose a non-linear mechanic for this?

While many mechanics are a choice of artistry, I believe in this case that using a non-linear curve is the only real valid decision. This is because of how the game will weaken if the mechanic was linear.

If claiming a length six was only twice as valuable as a length three, or length four vs. length two, then the player has no incentive for claiming the larger routes besides simply needing the route to connect to their destination.

But by having the route lengths award victory points non-linearly, the designer created an additional motivation: if you can manage to save your cards of a given color and claim one of the long routes, it can be a big payoff. This creates opportunities and decisions within the game — players have a reason to sometimes hold on to their train cards instead of simply spending them whenever a route looks promising. It is a strategy game, after all.

(Note that a length two route is worth exactly twice the points of a length one route. However, claiming a route two is not appreciably harder than a route one, so in this case a nonlinear step was likely unnecessary.)

Game Mechanic #4: Insurance Policies for Starships in Eve Online

Yeah, yeah — who wants to talk about insurance? But it is in a game, so it’s worth discussing because a broken mechanic here isn’t much different than a broken mechanic in say, combat.

Quick Description: In Eve online, you can purchase replacement insurance for your starships. If they get destroyed in a valid way (no self-destructs, thank you), the insurance company pays out Interstellar Kredits (ISK) based upon the value of your ship and the level of insurance you purchased.

Graph It!

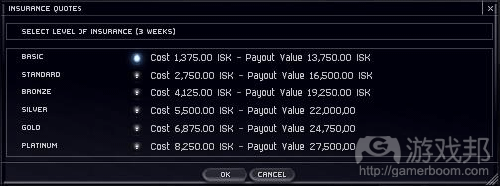
Here is a sample Insurance Policy choice screen:

Insurance Policy Options for a Starship in Eve Online

BTW, free insurance covers 40% of the ship value.

Let’s graph those numbers. In this case the “domain” (X value) is the purchase cost of the insurance and the payout value is the Y value. The game mechanic, or function, is the behind the scenes link between policy purchase cost and payout value.

Graph of a Insurance Options for a Starship in Eve Online

Dissect It!

As you can see, the mechanic is linear. Paying nothing gets you insured for 40% of the ship’s value. Paying 8,250 for this ship gets you insured for 99% of its value.

Why do you think the developers chose a linear mechanic in this case? What are the advantages or disadvantages of this over a nonlinear insurance schedule?

The starship insurance policies have a 12 week expiration. In what ways does the expiration time affect how the policy costs are structured?
Asymptotically Approaching the End of this Article

Linearity and non-linearity are core game system design elements I deal with on a daily basis. A simple choice of curve makes a huge difference in everything from control schemes to treasure drops.

Feel free to share any of your favorite mechanics or tips you’ve encountered in your own design jungle!

Game titles and images are trademark and/or copyright their respective owners. Used for journalistic purposes only. （source:gamasutra）