趣题：只用一把带有两条平行边的直尺作图

    在下面的问题中，你不能使用圆规，只能使用直尺作图。不过，你的直尺拥有两条平行边，你可以在作图时同时使用它们。你需要充分利用直尺的这个特点，完成下面几个作图任务。

      1. 作出已知角的角平分线；
      2. 作出已知线段的中点；
      3. 作出已知圆的圆心；
      4. 过已知点作已知直线的平行线。

    假设你的直尺是无限长的。直尺的宽度是固定不变的。直尺不能用来度量长度。

    1. 作出 ∠ABC 的角平分线。

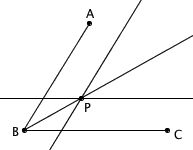
    如图，我们利用尺子的宽度，把角的两边各自都向内平移一个相同的距离，交点 P 与顶点 B 的连线就是角平分线。

    2. 找出已知线段 AB 的中点。

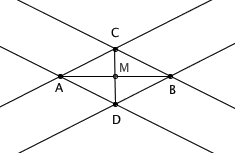
    如果 AB 的距离大于尺子宽度的话，很好办，我们把尺子卡在两点之间，用两种不同的方法作出过这两点的平行线。两组平行线交于 C 、 D 两点。容易看出，四边形 ADBC 是一个菱形，那么 CD 和 AB 的交点 M 就是 AB 的中点。事实上，我们不但作出了 AB 的中点，还顺带作出了 AB 的垂直平分线（一会儿会用到）。

    但是，如果 AB 的距离小于尺子的宽度呢？

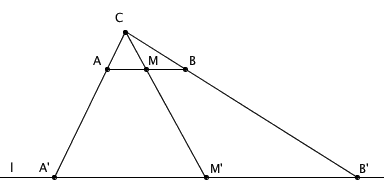
    如图，借助尺子的宽，作出 AB 的一条平行线 l 。然后，找出距离 AB 足够近的一点 C ，使得 CA 与 l 的交点 A' 以及 CB 与 l 的交点 B' 这两个交点之间的距离超过尺子的宽度。然后，用刚才的方法找出 A'B' 的中点 M' ，连接 CM' 与 AB 交于点 M ，M 就是 AB 的中点了。

    3. 找出已知圆的中心。我们只需要随便选取两条弦，作出它们各自的垂直平分线，两条垂直平分线的交点就是圆的中心。关键在于，怎样做线段的垂直平分线呢？下面我们就来讨论作出已知线段 AB 的垂直平分线的方法。

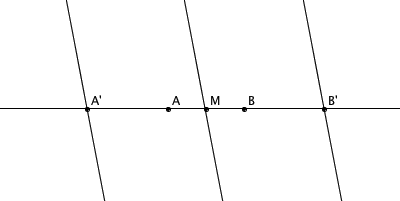
    当线段 AB 的长度大于尺子的宽度时，我们已经有办法作出它的垂直平分线了。如果线段 AB 的长度小于尺子的宽度，那么我们先作出 AB 的中点 M ，然后过 M 任意作一条直线。接着，借助尺子的宽度，把这条直线向左和向右平移相同的距离，与 AB 所在直线交于 A' 和 B' 。那么，A'B' 的距离就超过了尺子的宽度。作出 A'B' 的垂直平分线，它也就是 AB 的垂直平分线了。

    4. 已知直线 l 和直线外一点 P ，过点 P 作出 l 的平行线。

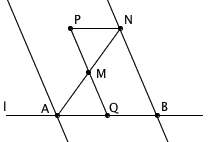
    我们先在直线 l 上任取一点 Q ，连接 PQ ，并找出 PQ 的中点 M 。然后，借助尺子的宽度，把 PQ 向左和向右平移相同的距离。假设 PQ 左边的平行线与 l 交于点 A ，连接并延长 AM ，与 PQ 右边的平行线交于点 N 。那么 PN 就是 l 的一条平行线。

 
    这个有趣的问题来自 1967 年 IMO 候选题。