44个精彩的物理趣题

    这个 Blog 几乎一直在讲数学趣题，却很少提到物理趣题。其实，我个人觉得，物理也是相当好玩的（我是化学不好才选的文科）。隐约记得初中搞物理竞赛时，曾见过大量让人大呼过瘾的好题。前几天看到了一个绝好的网站，里面有相当多的物理题目，让我激动了好一阵子。我搜集整理了里面的一些好题，加上了我自己的一些补充，在这里和大家分享。不过，由于我的物理实在不怎么样，如果出现什么错误，请大家及时纠正。

    那个网站上的“官方解答”并不见得靠谱，也不知是因为我没有悟到，还是因为它真的不靠谱。不管怎样，我给出的基本上还是它的官方答案。其实，阅读过程中你会发现，答案是次要的，真正有趣的其实是问题本身。

    几乎从没写过物理题目的 Blog ，想要用一篇文章总结物理趣题，因此毫无疑问——这是一篇非常，非常，非常长的文章。建议大家用自己喜欢的方式做个书签，一天看一点。如果觉得还不过瘾，推荐订阅物理大牛 EagleFantasy 的 Blog。

    另外，此日志一出，想必又会收到无数邮件，询问我作图用的什么工具的。在此就先回答了——请见 FAQ 。

    开始吧。

 
    有一块 V 字形木板，两侧与地面的夹角都是 θ 。一根密度均匀的绳子放在木板上，绳子与木板之间的摩擦系数为 1 。整个系统左右对称。没挨着木板的那段绳子所占的比例最大是多少？此时 θ 是多少度？

    用一些非常初等的方法可以得到，答案是 (√2 - 1)² ≈ 0.172 ，此时 θ = 22.5° 。具体解答可以见 http://star.tau.ac.il/QUIZ/05/sol_rope.pdf 。

 
 
    一个长、宽、高分别为 a 、 b 、 c 的长方体物块，斜靠在一个墙角。由于墙壁和地面都是完全光滑的，因此物块将会开始下滑。什么时候，物块会脱离墙壁？

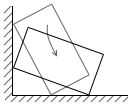
    为了解决这个问题，首先需要把物块和地面的夹角记作 θ ，物块下滑过程中的各种物理量都可以用 θ 来表示。然后，解决这个问题的关键就在于，当物块脱离墙壁时，物块向右的加速度就消失了，这个临界点就由等量关系 dv_x / dθ = 0 给出。不过，由此产生的方程非常复杂，我们只能用数值的方式去解它。

 
 
    有一个半圆柱体横放在水平桌面上，截面的半径为 R 。我们在半圆柱体上放一块木板，试图让它在半圆上保持平衡。假如这块木板非常薄，那么这块木板很容易放稳，即使有些小动静，木板也会自动恢复平衡。但考虑另外一个极端，假如这是一块非常厚非常厚的木板（甚至是大楼一般的形状），它显然不能稳放在这个半圆上。那么，这中间一定会有一个临界点。这个临界点在哪里？换句话说，这个半圆上最多能放稳一块多厚的木板？

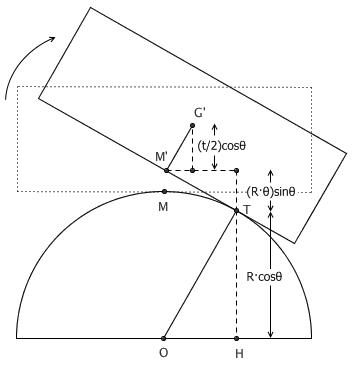
    把半圆的半径记作 R ，把木板的厚度记作 t 。如果把木板平放在半圆上，其重心的高度就是 R + t/2 。假如这块木板倾斜了一个微小的角度 θ ，那么图中 M'T 的长度等于弧 MT 的长度，即 2πR·(θ/2π) = R·θ 。此时，木板的重心 G' 的高度变为了 (t/2)cosθ + (R·θ)sinθ + R·cosθ。为了让木板保持平衡，不会自动往下滑，我们需要让新的重心高度大于原来的重心高度，即 (t/2)cosθ + (R·θ)sinθ + R·cosθ > R + t/2。解出不等式，再令 θ→0 ，即可得到 t < 2R。也就是说，一旦木板的厚度超过半圆的直径，木板就无法放稳了。

 
 
    假如你面向东边，站在冰面上，鞋底与冰面完全没有摩擦。你能否做出一系列动作，使得自己最后能面向西边站立？

    可以。只需要重复“伸臂－挥臂－屈臂”的动作，你的身体便会向反方向转动一点。期待实验党。

 
 
    用过多年的插座（尤其是插过大功率电器的插座），右边的孔（火线）往往会有过热的迹象。如果是劣质插座，加上经常插拔插头的话，右边的孔甚至会有烧黑了的痕迹。明明是通过相同大小的电流，为什么右边的孔会被烧得更厉害呢？

    目前，这个问题没有一个所谓的标准答案。当然，这个现象本身是否存在也是存疑的。大家不妨来说说自己家里插座的情况。

 
 
    呼拉圈是怎么转起来的？人应该做一个什么样的运动？呼拉圈的转动频率是由什么决定的？和人的体形、运动速度、运动方式有关系吗？是否存在一个最优的频率？⋯⋯

    我有几件事情死活搞不明白，吹泡泡是怎么吹出来的，小舌颤音是怎么发出来的，骑车不动把手是怎么实现拐弯的⋯⋯当然，还有呼拉圈是怎么转起来的。和呼拉圈有关的问题似乎永远也列举不完。如果你真的把它当成一回事仔细分析，你会发现这不是一般的困难。
    2004 年， Biological Cybernetics 上发表了一篇长达 15 页的论文，论文题目是 Coordination Modes in the Multi-Segmental Dynamics of Hula-Hooping 。这篇论文终于不负众望，成功地摘得了诺贝尔奖——当然，是搞笑版的。

 
 
    投一枚硬币，如果是正面，我就去打球，如果是反面，我就去打游戏，如果立起来，我就去学习。不知道大家第一次看到这个笑话时，有没有想过，如果一枚硬币真的有 1/3 的概率正面朝上，有 1/3 的概率反面朝上，有 1/3 的概率立起来，那么这个硬币的半径与厚度满足什么样的关系？

    这枚硬币必须满足，把它立起来后，即使倾斜 30 度仍然不倒。这样，硬币直立的“势力范围”才会达到 120 度。因此，硬币的直径应该是厚度的 √3 倍。

 
 
    考虑某颗星球，它由某种密度均匀的物质组成，其质量为 M ，体积为 V 。如果这颗星球是一个球体，那么它的半径 R = ((3V) / (4π))^1/3，星球表面上的重力加速度则为 g = GM / R² = GM((4π) / (3V))^2/3，其中 G 是万有引力常数。
    考虑这颗星球所有可能的形状，怎样的形状才会让星球表面的某一点重力加速度达到最大？最大值是多少？

    下图就是让表面某处的重力加速度达到最大的星球形状。这个图形是一个稍微有些变形的球体，整个图形是一个以 z 方向为轴的旋转体，顶端的 m 点即是重力加速度最大的点，它的重力加速度为 g = (4/5)(15/4)^1/3π^2/3M / V^2/3，只比球形星体的重力加速度大 2.6% 。这是又一个经典的例子——圆形似乎并不是那么完美。

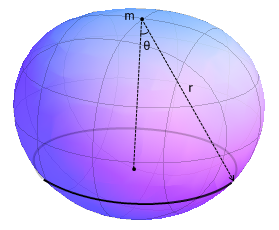
    这个问题的解法非常漂亮。首先，假设我们想要让星体表面上的某个点 m 的重力加速度最大，并且所受重力方向在 z 轴上，那么这个星体必然是沿 z 轴方向对称的。否则，取出不对称的一层，把多的部分填进少的部分让它变成一个完全对称的圆盘，这将会让 m 点在竖直方向上的受力变大。不断这样做直到这个图形沿 z 轴完全对称，显然就得到了一个更优的形状。
    接下来的步骤就真的神了。现在，在星体上取一个非常细的圆环，假设它的质量是 dM 。那么，这个圆环所贡献的重力加速度大小就是 G·dM·cosθ /r² 。如果把这个圆环从星体中挖掉，放到其它的位置上，那么新的圆环将会有新的 r 值和 θ 值。当整个形状达到最优时，这个形状将位于“极值点”的位置，也就是说它的“微分”为 0 ，任何微小的变动都不会改变 m 的加速度。这就意味着， cosθ / r² 是一个常数。这个条件就确定出整个星体的形状。

 
 
    Fermat 光程最短原理指出，光从 A 点到 B 点，总是沿着最快的路径传播。这一神奇的定律一下子就把直线传播定律、反射定律、折射定律统一在了一起。不过，后来我们知道了，更一般的描述应该是，光总是沿着光程处于驻点的路径传播。为什么会加上这一条？有没有光程极大的例子呢？

    这里有一个例子。考虑椭圆内的两个焦点 A 、 B ，和椭圆上的一点 M 。显然，不管 M 取在哪儿， AM + BM 都是相同的。现在，在椭圆内部画一条曲线，这条曲线与椭圆相切于 M 点。然后，擦掉原来的椭圆，把这条曲线视作镜面。显然， AMB 仍然是一条反射光线，但从其它地方反射，光程都会小于 AMB 。 AMB 是一个光程极大的路径。

 
 
    物理量的单位总是由基本单位（质量、长度、时间等）的幂相乘得来的。比如，能量的单位就是 1J = kg·m²·s^-2 。为什么没有什么物理量，它是由基本单位通过更复杂的形式导出的？比如说，为何没有什么物理量，它的单位是 sin(kg)·log(m) ？

    这是一个非常有趣，无疑也是非常深刻的问题。它让我们开始认真思考一个看上去很不像问题的问题：什么是物理量？什么是物理单位？我们需要去挖掘物理量和物理单位的最基本、最本质的性质。
    网站上的标准答案是，只有这种形式的导出单位才能保证，在不同的单位制下，得到的导出单位是等价的。
    具体地说，物理单位的作用就是用来描述，当各个基本单位的尺度变化以后，这个物理量会发生怎样的变化。比如说，密度单位是质量除以长度的三次方，就表明如果质量扩大到原来的 2 倍（或者说单位量变成了原来的 1/2 ），长度扩大到原来的 4 倍（或者说单位量变成了原来的 1/4 ），那么这个物理量将会变成原来的 2/4³ = 1/32 。
    现在，假设某个物理量的单位是质量的正弦乘以长度的对数。按照国际标准单位制，这个单位是 sin(kg)·log(m) 。假如单位换成了 sin(g)·log(cm) ，那么这个物理量将会变成原来的 sin(1000)·log(100) ≈ 3.80792 。再继续换算成 sin(mg)·log(mm) ，物理量应该继续变成原来的 sin(1000)·log(10) ≈ 1.90396 。但是，如果从 sin(kg)·log(m) 直接变到 sin(mg)·log(mm) ，物理量应该变成原来的 sin(1 000 000)·log(1000) ≈ -2.41767 ，这就和前面的结果矛盾了。利用一些微积分知识可以证明，如果一个合成物理单位不会出现这样的问题，它必然是基本单位的幂的乘积的形式。
    不过，这个解释并不能让我十分满意。大家怎么看呢？

 
 
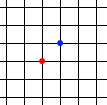
    有一个无穷大的正方形网格，每条小线段都是 1Ω 的电阻丝。求相邻两点间的等效电阻阻值。

    这个问题有一个很妙的解法。假设一个大小为 1A 的电流从红点处流入，从各个无穷远处流出。由对称性，有 (1/4)A 的电流将会流过红蓝两点之间的线段。现在，再假设一个大小为 1A 的电流从各个无穷远处流入，从蓝色点流出。由对称性，红蓝两点之间的线段仍然有 (1/4)A 的电流。现在，把两种情况叠加在一起看，大小为 1A 的电流从红点进去从蓝点出来，那么，红蓝两点间的线段就有 (1/2)A 的电流。因而，两点间的电压就是 (1/2)A·1Ω = (1/2)V 。因而两点间的等效电阻就是 (1/2)V / 1A = (1/2)Ω。

    说到无穷网格电阻的问题，我们有说不完的话题。这个问题本身的扩展非常之多。例如，我们可以把问题扩展到 N 维的情形：N 维无限电阻网格中，相邻两点的等效电阻是多少？利用同样的方法可以得出，答案就是 1/N。

    回到二维情形，如果我们换一个扩展方向，改问对角两点间的电阻，上述分析方法就不行了。而这个加强版问题的答案也更加玄妙：两点间的阻值为 (π/2)Ω 。大家可以在网上很多地方查到这个加强版问题的解法。

    xkcd 有一个经典漫画，形象地描绘出 nerd 们被数理趣题折磨的感受。当然，这幅画本身也折磨了不少人，网上涌现出大量对这个问题的讨论。

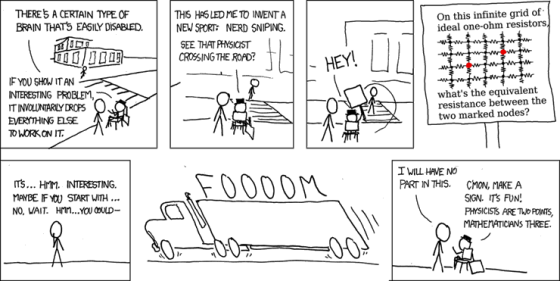
    还有一种经典的无穷电阻问题：一个向右无穷延伸的梯子形网格，每条线段都是 1Ω 的电阻，求两点间的等效电阻。

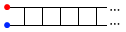
    问题的解法非常漂亮。假设我们要求的答案是 R，则 R 可以看作是三个 1Ω 的电阻串联，然后把一个阻值为 R 的电阻（也就是它本身）与中间那个 1Ω 电阻并联所得。于是得到等量关系 R = 1 + 1/(1+1/R) + 1，解得 R = 1 + √3。

    还有一些经典的求电阻问题。其中一个问题是，一个正方体的 12 条棱上各有一个 1Ω 的电阻，求距离最远的两个顶点之间的等效电阻。 2007 年 10 月份 IBM Ponder This 的题目则是，分别考虑五种正多面体，如果每条棱上各有一个 1Ω 的电阻，则相邻两顶点的等效电阻是多少？巧妙地利用对称性，这几个问题都可以迅速被秒杀。

 
 
    假设有一个圆锥形的冰山，冰山表面绝对光滑。你打算把一个绳圈套在山尖上，然后沿着绳索爬上去。考虑两个极端情况：如果冰山特别尖，顶角特别小，这个计划自然不成问题；但若冰山特别“肥”，顶角特别大，向下拉绳子后，绳圈将会滑出山尖。这中间一定有一个临界点，也就是绳圈掉不出来的最大顶角。这个顶角是多大？

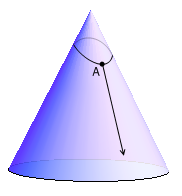
    这是一个非常有趣的问题。问题的本质就是，绳圈在怎样的圆锥面上才存在“被拉紧”的稳定状态。容易想到，绳子被拉紧，意味着绳圈从 A 点出发，将沿最短路径绕过山尖一周，再回到 A 点。如果把圆锥的侧面展开成扇形，绳圈其实就像下面这样（图中的 A 点和 A' 点在圆锥上是同一个点）。

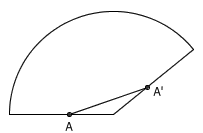
    显然，当这个扇形的顶角小于 180 度时，这样的绳圈才可能存在；而当这个扇形的顶角大于 180 度时，拉紧的绳圈就会滑到山尖外面去。据此不难推出，所求的临界情况就是，圆锥的高与母线的夹角为 30 度。

 
 
    n 块相同的木板重叠，最多能够伸出桌面多远？

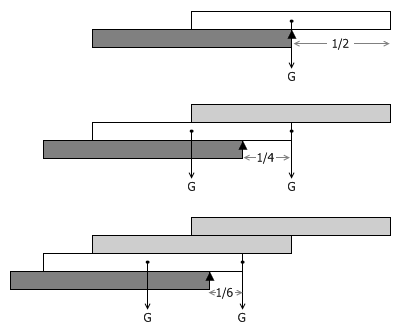
    这是一个非常经典的问题。传统的答案是，把第一块木板的重心放在第二块木板的右边缘，把这两块木板的重心放在第三块木板的右边缘，把这三块木板的重心放在第四块木板的右边缘⋯⋯利用杠杆原理可以推出，如果每块木板都是单位长，那么 n 块木板可以伸出桌面 (1 + 1/2 + 1/3 + … + 1/n) / 2 个单位的长度。由调和级数的性质，我们立即可以得知，只要木板数量足够多，木块伸出桌面的长度是没有上界的，想伸出去多长就能伸出去多长。但同时，这个增长速度也非常缓慢⋯⋯ 20 块木板只能伸出大约 1.79887 个单位的长度， 1000 块木板也只能伸出大约 4.8938 个单位的长度。

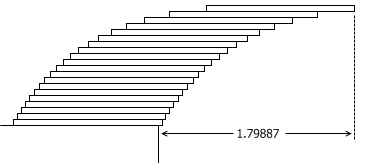
    不过，采用一些其它的方案（比如拿几块木板在后方作为“配重”），我们可以让木板伸出的长度更远。下面是一篇非常经典的论文，总结了目前对这个问题的研究结果： http://arxiv.org/abs/0707.0093 。

 
 
    上楼时，人克服重力做功，需要耗费很多能量。但是，在平地上行走时，人并没有做功。那么，为什么我们走路时还要耗费能量呢？

    1999 年 3 月的 Scientific American 上说到，其实在步行时，我们也是要克服重力做功的。这是因为，在步行的过程中，人的重心会一上一下地摆动。当两腿一前一后着地时，人的重心偏低；而单腿着地迈步时，人的重心会升高大约 3cm 。我们走路的能量主要就消耗在了这里。
    当然，事实上，即使人不走路，光是原地站着，也是要耗费能量的（大约为 80W ）。假设人的步行速度是 v ，那么步行所用的能量可以用公式 P = 80W + K·v 大致算出，其中 K·v 就是步行过程中耗费的能量，系数 K 大约为 160N 。
    教中学物理最怕聪明孩子，一些古怪的问题常常会让老师也支支吾吾答不上来。初中物理中，有几个最不好给学生解释的事情。走路不做功，为什么还要耗费能量？电流从电厂来又回到电厂去，为什么我们还要支付电费？把装满水的水杯不盖纸片直接倒过来，为什么大气压没有把水支撑起来？拳头打在墙上后将会受到墙给拳头的反作用力，但若拳头挥空了，这个力的反作用力是什么？
    你都打算怎么解释？

 
 
    橄榄油的沸点是 300℃ ，锡的熔点是 231.9℃ 。为什么我们能在锡锅里炸东西？

    答案：橄榄油并没有沸腾，沸腾的其实是食物里的水。而且，正是食物里的水才让橄榄油和锡锅都保持在 100℃ 。如果食物里的水被烧干了，食物就会被烧焦，锡锅当然也会被烧毁。

 
 
    在晃动的火车车厢上，把一瓶水放在小桌子上。如果想让这瓶水放得更稳，有一个极其简单的方法。这个方法是什么？

    答案：喝掉一部分水，让整瓶水的重心下降。
    注意，这里又有一个有趣的极值问题。如果瓶子里装满水，整个系统的重心显然要比只装有一部分水时更高；但若把水全部喝掉，只剩一个空瓶子，整个系统的重心仍然会比有一部分水时高。建立模型，求出使得整个系统重心最低的水位高度，是一个绝佳的物理课题。
    有一个蛮有意思的结论：当整个系统的重心达到最低时，水位一定和此时整个系统的重心高度相同。其实这个很好理解：当水位没有达到整个系统的重心高度时，每加一点水，都相当于在重心下方填充质量，让重心下降；但水位高度超过了整个系统的重心，则每加一点水，都相当于在重心上方新添质量，重心便会开始上升了。

 
 
    12 节 1V 的电池首尾相接，然后将一块电压表如图连接。电压表的示数是多少？

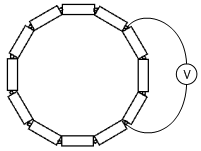
    有时候，方言的力量真是强大。看到这个题目后，我脑子里闪过的第一个形容词就是重庆话“想得出来”，但始终没找到合适的普通话替代词。总之，这题可以说是非常具有想象力了。
    答案是 0V 。假设每个电池的内电阻是 R ，这个回路的电流就等于 12V 除以 12R ，即 (1V)/R 。于是，每个电池的内电压就是 R·(1V)/R = 1V ，而这恰好是这个电池的电动势。因此，每个电池的外电压都为 0 。对于一组连续的电池来说，这个推理同样成立。

 
 
    为什么跳蚤、蚱蜢、人和狮子，尺寸差异那么大，但能跳起的最高高度都是 1 米左右（最多相差一个不超过 2 的系数）？

    看到这个问题之后，我在 Google 里搜了一下，竟然真是这样。猫猫狗狗老鼠老虎，可以跳起的高度都在 1 米这个尺度左右——猫猫和狗狗都能跳 1 米左右，老鼠能跳 40 厘米，老虎能跳 2 米。你以为袋鼠牛 B 吗？其实袋鼠也只能跳 2 到 3 米高。注意，这里的跳起高度并不是指“手能摸到的高度”，而是生物让自己重心升高的高度。
    有人可能想到了原因。一个动物身体小，力量也小，但正因为它身体小，跳起 1 米也不需要太大的力。反之，大型动物力量倒是大，不过要跳起来确实也需要很大的力。这就让动物们能够跳起的高度变得平衡。
    不过，为什么这两个因素能够平衡，而不是一个压过另一个呢？假设生物的形体和密度都相近，我们就可以漂亮地证明这一点：把一次跳跃中足部可以提供的能量记作 E ，生物自身的重量则记作 W ，那么生物跳起的高度应该正比于 E/W 。如果再把生物的尺寸（一维上的长度，比如身长）记作 L ，那么 W 是与 L³ 成正比的。而 E 则等于肌肉提供的力乘以这个力能够牵引的肢体运动距离，其中前者与肌肉的横截面积成正比，也就与 L² 成正比，后者和足部长度成正比，也就是和 L 成正比。因此， E 和 L³ 成正比。于是， E/W 与 L 无关！
    小时候大家应该都听说过，跳蚤巨牛无比，能跳起 1 米多高，是自身高度的 100 多倍。原来，不管什么都能跳起 1 米多高，这个倍数关系这么惊人，只是因为跳蚤自己太矮罢了。

 
 
    一个空心正方体的内部有六面墙。能否让一个小球在每一面墙上都各反弹一次，最后又回到出发点（假设没有重力）？

    可以。这是由 Hugo Steinhaus 首先发现的。注意，每反弹一次，只会让速度中的其中一个分量变为相反数，因此六次反弹后，速度向量会和出发时相同。为了让六次反弹后还能回到出发点，我们只需要再让各段路程的长度都相同就行了。上图中的方案里，每段路程都是一个小立方体的对角线，因而最后就正好能回到原点。

 
 
    一个物块从高度为 h 的光滑斜面顶端开始下滑，下滑到底端后沿光滑水平面以速度 v 匀速直线运动下去。初始时，物块的重力势能为 mgh ；到了斜面底部后，重力势能为0，完全转化为了动能 (1/2)mv²。由此我们可以解出， v = √2gh 。
    现在，假设你坐在一个以 v 的速度向右做匀速直线运动的车里。如果以你为参照物，你将会看到，斜面顶端的物块初始时机械能为 mgh + (1/2)mv²，而到了斜面底端后，机械能突然变成 0 了！这该怎么解释呢？

    这是一个非常漂亮的问题，大家不妨多想一想。简单地说，就是在新的参照系下，物体并不是沿着直线下滑，斜面也对物体做功了。不过，这只能解释一部分“消失”的机械能。具体答案在 http://star.tau.ac.il/QUIZ/99/A07.99.html。
    有网友来信说，从根本原因上看，只要把斜面本身也算进系统里，考察斜面的能量，就不会产生不守恒的问题了。

 
 
    有一段横截面是等边三角形的木头，密度为 0.5g/cm³ 。它在水中漂浮时，哪头会朝上？

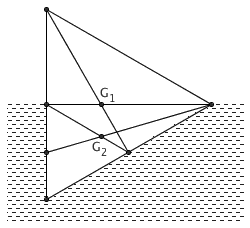
    答案：如图所示，漂浮时，它的其中一条中线一定和水面重合。这是因为，通过计算可知，此时整个物体的重心 G₁ 和浸入水中的部分的重心 G₂ （也就是浮力的作用点）正好在同一竖直线上，并且高度差达到最小值。

 
 
    20 世纪初，一本名为 Power 的杂志上曾经登载了这样一个永动机模型。如图，把光滑绳圈套在滑轮上，绳圈右侧浸在水中。于是，绳圈右侧将持续受到一个竖直向上的浮力，绳子便逆时针转动了起来。
    这个永动机模型可行吗？如果不可行，问题出在哪儿？

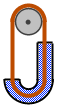
    答案：废话，当然不可行。可是，这个模型错在哪儿呢？注意，浮力其实是物体上下表面的液体压强差产生的。因此，浮力只会出现在完全浸入液体，或者漂浮在液体表面的物体上。在这个例子中，绳子并不会受到浮力。如果你把绳子想像成是一片片圆盘拼成的，每个圆盘都只受到侧面来的液体压强，在绳子的方向上是不可能有力产生的。
    围观更多的永动机，请移步 http://en.wikipedia.org/wiki/History_of_perpetual_motion_machines 。

 
 
    秤上放着一个玻璃瓶子，瓶盖是密封的。一只苍蝇飞在瓶子中，没有挨着瓶子。秤的示数等于瓶子的重量，还是大于瓶子的重量？如果苍蝇靠栓在身上的一个小氢气球浮在瓶子中呢？

    这是一个经典问题了。对于前一个问题，秤的示数应该大于瓶子的重量，多的这点重量正好就是苍蝇自身的重量。这是因为，苍蝇要想飞起来，必须要给空气一个等于自身重量的向下的力（从而获得一个等于自身重量的向上的力）。空气将会把这个力传到瓶底，也就是对瓶底施加一个相同的力。
    对于第二个问题，答案是，秤的示数就等于瓶子的重量。如果苍蝇受空气浮力悬浮在空中，我们就可以把苍蝇连同气球所占据的位置等价地用空气来替换，毕竟瓶子里悬浮着一只气球苍蝇和悬浮着一坨空气没什么两样嘛。这样看来，秤的示数就是瓶子的重量了。
    这个问题扯开来，也有一大堆可以说的。初中物理有一道经典题目：把一杯水放在秤上，然后手指伸进水里（手指未碰到杯底，水未溢出），问秤的示数怎么变。答案是，变大了。因为水位升高，对杯底的水压增大了，从而杯底受到的压力也就增大了。当然，按照之前的思路，我们还有一个更好的解释。你的手指受到了一个竖直向上的浮力，水自然也就受到了一个竖直向下的反作用力，这个力的大小就等于手指排开水的重量。因此，你可以把手占据的位置替换成一堆水。可见，杯子里的水量相当于是凭空增加了，秤的示数自然也就增加了。
    大家估计听过一个脑筋急转弯，说一个独木桥载重 80 公斤，为什么一个重 70 公斤的人可以拿着两个各重 10 公斤的球过桥？答案是，这个人像杂技演员一样，轮流把球扔到空中，保证手里只有一个球。不过大家仔细想想便会发现，这个题明显有 bug 。你需要给球一个大于 10 公斤的力，才能让球加速上升；此时，球会给你一个大于 10 公斤的反作用力，这样就超过独木桥的载重了。

 
 
    云是由小水滴组成的。水的密度是空气密度的 800 多倍。为什么云不会掉下来？

    我操，这个问题太有型了！我在反省自己，为什么小时候听说“云是由小水滴组成的”的时候，没有提出过这个问题呢？
    这个问题的答案是，云就是会往下掉的，只不过下落的速度非常慢⋯⋯
    云中的小水滴颗粒极小，因而小水滴受到的空气阻力，其数量级和自身重力相当。计算可知， 1 微米的水滴下落速度约为 0.13 毫米每秒，也就是一天下降 11 米。即使是 10 微米的水滴，下落速度也很慢，大约每天 1.1 千米。如果不精确测量的话，我们是没办法观察到的。详细计算过程可以见这里： http://star.tau.ac.il/QUIZ/98/A10.98.html 。
    这让我想起一个冷知识：蚂蚁是摔不死的，因为空气阻力和自身重力相当。这又让我想起一个冷笑话：蚂蚁从摩天大楼摔下去，是怎么死的？答案是——饿死的。

 
 
    利用蹦床一次，你可以跳到多高？

    答案：两倍原地起跳的高度。蹦床自己既不会消耗能量，也不会提供能量，因而你跳到蹦床上以后，蹦床储存的弹性势能只能把你弹回到一次起跳的高度。你在蹦床上再跳一次，便能跳到两倍高。

 
 
    大家在电影的各种爆炸场面里都会看见这样一个情景：一个正在倒下的烟囱，在倒下的过程中，会自己断成两截。断裂处将出现在烟囱的什么位置？
    这是 MIT 的一道入学考试题。

    这个问题很漂亮。在断裂之前，整个烟囱显然以一个相同的角速度在下落。考虑烟囱的顶部，由于自身重力的影响，它本来应该下落得更快，但却被强行地“扳”回到一个和烟囱下部相同的角速度。这使得烟囱最终发生断裂。计算可知，断裂将发生在烟囱的 2/3 处。更技术的分析请看 http://star.tau.ac.il/QUIZ/96/A07.96.html 。

 
 
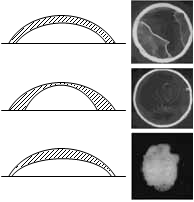
    为什么床单、被罩、桌布上的污渍都是这种形状？

    相信大家都曾经遇上过这样的现象吧。这个问题要解释起来，还真不容易——网上提出此问题后，无一人答对。很多人都说，液体中含有什么什么，布料里含有什么什么等等。其实，这种现象是很普遍的，它与布料、溶剂、溶质都没关系。这种现象真正的原因，是和液体蒸发的模式有关的。如果液体表层蒸发了，液体会向外展开，填充刚刚流失的部分。其结果就是，液体会不断地向边缘涌去，造成了边缘痕迹堆积。

    对几种不同的蒸发模式进行模拟，可以看到不同的污渍形状，进而很好地说明了上述推测的正确性。

 
 
    为什么水渍是深色的？

    这是个好问题呀！我们每天都会遇上这样的事情，已经习以为常，却从来没有想过为什么。真要问个为什么，嘿，还真不好回答。
    在网站上，这个问题同样无人答对。根据布料的不同，官方给出了两种解释，大家可以去看看： http://star.tau.ac.il/QUIZ/96/A11.96.html 。

 
 
    最后，附上一些我以前收集的一些漂亮的物理谜题。

 
 
 
    你现在正位于赤道，此时太阳刚刚升起。你要用一把激光炮轰炸太阳中心。你应该瞄准什么地方？

    你应该瞄准太阳的中心。有人会说，不对呀，阳光不是会被大气层折射吗？但是，你射出的激光也会被折射，由于光路是可逆的，因而你就该瞄准你看到的太阳。有人会说，还是不对呀，太阳光射到地球需要 8 分钟，你看到的太阳是 8 分钟前的太阳，现在太阳已经不在原来的位置了呀？你又被坑了——太阳是不动的，动的其实是地球。

 
 
    用天平测量物体的重量（准确地说，是质量）时，如果砝码有磨损，那么测量结果会偏大还是偏小？仔细想想吧，这题很容易答错。

    这是初中物理最阴险的陷阱题目之一。绝大多数人会认为，既然砝码被磨损了，没有它标识的那么重了，那么测量结果一定是偏小了。答案恰恰相反，如果砝码有磨损，测量结果应该偏大了。 正因为砝码没有它标识的那么重，所以我们才需要在天平上添加更多的砝码让它保持平衡。因此，测量出来的结果会更大一些。

 
 
    用一盆水，一张纸，一台电子秤，如何测量一个给定排球击打在地上对地的作用力有多大？

    首先把纸张铺在地上，在排球上蘸水，然后对着地上的纸击打。这样一来，纸上便留下了一个圆形的水印。然后，把印有水的纸铺在电子秤上，把排球放在纸上，一点一点向下挤压排球，直到排球的下底面与水印重合。此时，电子秤上的示数也就是排球击打在地上时的作用力了。
    这是间接测量实验设计问题中让人拍案叫绝的一道好题。

 
 
    一个人站在湖里的一艘船上，把一颗石子扔进湖里。湖水的水位将会发生怎样的变化？

    答案：湖面将会变低。这是一个非常经典的初中物理问题。由浮力公式，物体所受的浮力等于它排开水的重力。初始时，船、人、石子都在水面上静止，他们的总浮力（也就是总的排开水重量）等于总重力；但石子投入水中后将会沉底，它所受到的浮力小于它的重力，因此船、人、石子的总浮力（同样即为排开水的总重）小于他们总重力。也就是说，排开水的总量减少了，因而水位将会下降。
    这是最标准的解法。每次讲到这个问题时，我都喜欢讲讲另外一种直观的理解方法。不妨把这个将会被投掷出去的石子悬挂在船的底部。由于漂浮在水面上的船、人和石子的总重力不变，因此总的排开水重量也不变，这样的假设不会改变水位高度。现在，把悬挂石子的绳子剪断，于是石子下沉，船会上浮一些，致使水位下降。

 
 
    两根一模一样的金属棒，一根是磁铁，一根是普通的金属棒。没有其他工具，怎样把他们区别开来？

    把他们摆成一个 T 字形。如果相吸，竖着的就是磁铁；如果没有相吸，横着的就是磁铁。
    磁铁中部几乎没有磁性。

 
 
    为什么镜子里的东西是左右颠倒的，不是上下颠倒的？

    这是一道经典智力题了，镜子问题、羊与车问题和 0.9999… = 1 的问题可谓是引发口水战的三大法宝。哪个论坛想要增加人气的话，把这三个问题挨着发一遍就行了。问题的答案是，镜子里的东西既不是左右颠倒，也不是上下颠倒，而是前后颠倒的。不过，人们似乎并不喜欢接受“镜像”的概念，总爱拿镜子里的东西跟实际的东西来比。但是，两个镜像的东西怎么转都不能完全重合，于是纠结的事情就发生了。如果你想象镜子里的东西水平转 180 度转回去，这并不能和实际物体重合，每个东西都左右颠倒了。如果你想象镜子里的东西竖直方向转 180 度，这样也不能和镜子前的物体重合——左右倒是没问题，但上下就颠倒了。不过，人们生活在一个水平面上，人本身的对称轴正好又是竖直方向上，因此人总是习惯性地采用了前一种思维。
    为了摆脱传统思维的束缚，不妨假设镜子前的物体是一个三角形什么的，想象起来就会方便多了。
    Geek 小美女 localhost_8080 曾对左手右手左手系右手系左右颠倒左右镜像纠结过很久，她曾在 Twitter 上提过一个非常有趣的问题：某地外生命在飞船中，你只能用无线电与它交流，如何通过口头描述指导它在一双手套中分辨出右边的那一只？
    你打算怎么办？