动物们的爱情

动物们的爱情就是为了交配生孩子。从生物学的角度来说，不管是雄性还是雌性都可以用相同的标准评价自己的在这方面的成就：看看自己有多少后代可以发育成熟。

就像英国动物行为学家 理查德•道金斯 （Richard Dawkins）说的那样：父母们可以相互合作共同抚养这些孩子。但如果其中某一方付出的比对方少，他或她就会有更多的资源用于同其他性配偶所生的其他子女身上，以获得更多的繁殖机会。因此，每个配偶都设法利用对方，迫使对方多“投资”一些。就个体来说，称心如意的算盘是，“希望”同尽可能多的异性成员进行支配，而让与之交配的配偶把孩子抚养大。

雄性在这方面占据一定的主动权，因为他只要把雌性骗“上床”命中后，就可以选择离开了。但是，雌性个体也并非没有办法，通常雌性是被追求的对象，她有王牌——拒绝和不靠谱的雄性交配。在交配之前，雌性配偶就有很多策略选择，比如好好考察雄性一番，选择一个最可靠的配偶。

这无疑是一场博弈游戏。《自私的基因》中就提到一个有趣的 简化模型 ，来描述这种情况，把雌性分为谨慎型的和轻浮型；把雄性分为责任型和风流型。谨慎的雌性不爱花花公子，只有在雄性经过长时间的追求后，付出一定努力和耐心取后才会同意“交往”；而轻浮的雌性则不放过可能的交配机会，去尽量多地繁衍后代。

在两类雄性群体中，责任型的雄性看上某位后，就会准备长时间地追求，且交配后仍同她待在一起，共同抚养后代。而对于风流的雄性个体来说，如果雌性个体不立即同其进行交配，他很快就会失去耐心，走开并另寻目标，即使交配之后，他们也不会留下承担起作父亲的责任，而去另寻新欢。

两性的博弈策略

让我们把这场“爱情”当成一种支出和收入的游戏，看看量化后的结果是怎样的。设生育一次后代，双方各得15；将后代抚养长大则需要耗费 20；倘若双方都是“认真的”，可以看成双方各需付出 10。此外，谨慎的雌性和责任型雄性在一起之前会有一个漫长的过渡期，双方在这段时间里会相互考察（主要是雌性考察雄性），建立信任关系。所以有理由设这个“暧昧”的过程双方各需付出 3 的时间成本。当谨慎的雌性碰到花心的雄性时，花心雄性没有足够的耐心度完过渡期，所以他们不会诞生爱情，双方既没有损失也没有收益。

当轻浮型雌性碰到责任型雄性时，因为他们不用考察，因此每抚养一个幼儿，双方净收益都为 15 – 10 = 5。但当轻浮型雌性碰到风流型雄性时，雄性个体在“搞定”这个雌性后就不受约束地离开了。只留下雌性独自和幼儿挣扎着生活下去，承担起 －20 的全部代价。一个轻浮的雌性个体结交一个风流的雄性个体，其净收益就为 15－20 = －5；而这个风流的雄性的收益却是 15。

因此，雌性的支付矩阵如下：

设雄性中责任型的比例是 x。这时候，谨慎型雌性的平均收益是 2x + 0（1 - x）= 2x。轻浮型雌性平均收益为 5x – 5（1 - x） = 10x - 5。当 x = 5/8 时，不同类型的雌性在这场游戏中的收益刚好相等。可以看到，当责任型雄性比例超过5/8 时，对谨慎型雌性有利，否则，轻浮的雌性在这场博弈中就要收获更多了。

而雄性的支付矩阵是：

假设雌性中谨慎型的比例是 y。此时，责任型雄性的平均收益是 2y + 5 (1 - y) = 5 – 3y，而风流型雄性的平均收益则是 15 - 15y。当 y = 5/6 时，二值相等。当谨慎型的雌性比例超过5/6时，责任型的雄性可以获利更多，否则风流的雄性更占便宜。

进化上的稳定策略

有趣的是，x的值和y的值不是独立存在的，它们互相干扰，并构成一个循环。如图。

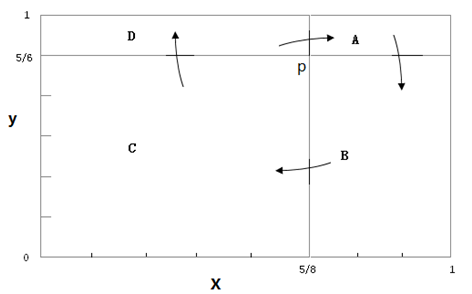
其中横坐标代表责任型雄性所占比例，纵坐标代表谨慎型雌性所占比例，任意一点代表全体成员的构成比例。如果 5/8 的雄性是责任型的，同时5/6的雌性是谨慎型的，则成员比例对应与 p 点，此时构成的比例稳定。但假设成员的构成比例是对应 A 区某点的，由于责任型雄性比例很高，对轻浮型雌性来说，她们很容易找到一个好父亲，而不必支付考察期带来的成本 3。同谨慎型雌性相比，它就要多收益 3 个单位。轻浮型基因因此散布开来，成员比例被改变，进入 B 区某点。

在 B 区，谨慎型雌性比例较低，这无疑给风流的雄性们提供了绝佳的“猎艳”环境。他不会对要抚养的幼儿付任何代价，却能收益 15 个单位，风流雄性的基因就会随之蔓延。

风流雄性数量如果迅速壮大的话（C 区），形势对轻浮型雌性就很不利，这时候，谨慎的雌性则会重新占据有利条件，她坚持拒绝风流的雄性，虽然没有收益但也至少不会有损失，这比损失惨重的轻浮型雌性要好很多。其结果就是，谨慎型雌性的队伍开始壮大，成员比例进入 D 区。

在D区，由于谨慎型雌性数量众多，风流的雄性不受欢迎，在求偶过程中到处碰壁。责任型雄性的优势在此时体现出来，队伍开始重新壮大，使得成员比例重新回到 A 区。

但实际上，这种无休止的循环很难出现。因为存在一个稳定点，当 x = 5/8，y = 5/6 时，种群的遗传是稳定的。上述的循环表明的其实是：某一性别的成员偏离这个稳定比例时，就会被另一性别在策略比率上的相应变化所针对，从而对原先的偏离产生不利影响。这也就是进化上的稳定策略（Evolutionarily Stable Strategy）。

这个模型适用于人吗？

那这个模型能不能应用到人的身上呢？答案是，不能。

动物和人的行为有一定的相似性，具体到人身上，上述模型有一定参考价值。但毕竟人的行为是复杂而难以琢磨的，更重要的是，自然界中动物们的行为准则受基因控制，而人类则具备足够的力量去抗拒那些与生俱来的自私基因，并且还会受到道德伦理等社会准则的种种约束。

具体到恋爱中，因为种种原因，人们对爱情的观点也不尽相同，比如有的人由于对某位异性的异常喜欢，并不会计较付出多少和最终能收获什么；有的人则很“博爱”，只要看上就会去追求；有的人则会选择喜欢同性等等……恋爱中的人多数都是在享受这种美好的感觉，不会太计较得失。风流和责任，谨慎和轻浮，更多的可能是出于个人情感的选择，并非策略。所以，如果你真要谈恋爱，一个好的建议是：那就好好谈恋爱吧。

本文选取了《自私的基因》中一个有趣的案例，对两性之间的博弈做了一个有趣的计算和分析，更多的是想介绍这个博弈中的稳定和平衡。至于最后一部分关于恋爱的论述，作者经验基本“欠佳”，可能不很到位。就当是抛砖引玉，请大家各抒己见吧。

PS：关于人们在爱情中的行为策略，死理性派将会在最近一个特殊的日子里发表“专家级”见解，为广大单身群众排忧解难，请关注哦。

本文的案例来源自《自私的基因》

相关阅读：

《明知其输而博赢的概率分析》

一夫一妻 生就如此？