风险控制：信用评分卡模型

什么是信用评分卡模型？

评分卡模型又叫做信用评分卡模型，最早由美国信用评分巨头FICO公司于20世纪60年代推出，在信用风险评估以及金融风险控制领域中广泛使用。银行利用评分卡模型对客户的信用历史数据的多个特征进行打分，得到不同等级的信用评分，从而判断客户的优质程度，据此决定是否准予授信以及授信的额度和利率。相较资深从业人员依靠自身的经验设置的专家规则，评分卡模型的使用具有很明显的优点：

• 判断快速：系统只需要按照评分卡逐项打分，最后通过相应的公式计算出总分，即可准确判断出是否为客户授信以及额度和利率。
• 客观透明：评分卡模型的标准是统一的，无论是客户还是风险审核人员，都可以通过评分卡一眼看出评分结果和评判依据。
• 应用范围广：由于评分卡的评分项是客观计算，其得出的分数具有广泛的参考性和适用性。例如，生活中常见的支付宝芝麻信用分，就是依据评分卡模型计算得出。

评分卡模型在银行不同的业务阶段体现的方式和功能也不一样。按照借贷用户的借贷时间，评分卡模型可以划分为以下三种：

• 贷前：申请评分卡（Application score card），又称为A卡
  • 更准确地评估申请人的未来表现(违约率)，降低坏帐率
  • 加快(自动化)审批流程, 降低营运成本
  • 增加审批决策的客观性和一致性，提高客户满意度
• 贷中：行为评分卡（Behavior score card），又称为B卡
  • 更好的客户管理策略, 提高赢利
  • 减少好客户的流失
  • 对可能拖欠的客户，提早预警
• 贷后：催收评分卡（Collection score card），又称为C卡
  • 优化催收策略，提高欠帐的回收率
  • 减少不必要的催收行为，降低营运成本

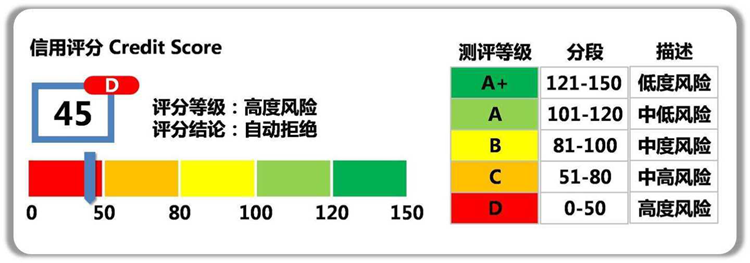
评分卡模型示例：

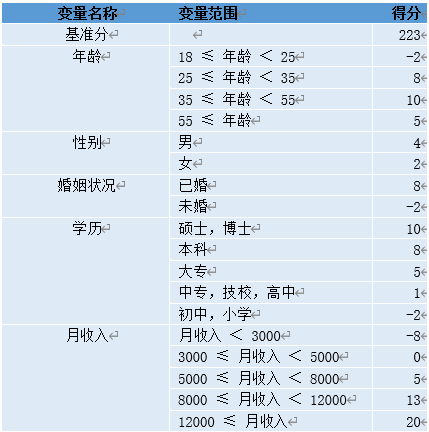
一个用户总的评分等于基准分加上对客户各个属性的评分。举个例子某客户年龄为27岁，性别为男，婚姻状况为已婚，学历为本科，月收入为10000，那么他的评分为：223+8+4+8+8+13=264

如何搭信用评分卡模型？

有了上面的评分卡示例，接下来需要考虑的是如何生成类似上面的表格：

• 变量特征是如何选取的？
• 特征的变量范围是如何进行划分的？
• 每个字段的分值是如何设定的？

变量选择

变量筛选的主要目的：

• 剔除跟目标变量不太相关的特征
• 消除由于线性相关的变量，避免特征冗余
• 减轻后期验证、部署、监控的负担
• 保证变量的可解释性

单变量筛选

单变量的筛选基于变量预测能力，常用方法：

基于IV值的变量筛选

• WOE的取值范围是[-∞,+∞]，当分箱中好坏客户比例等于整体好坏客户比例时，WOE为0。
• 对于变量的一个分箱，这个分组的好坏客户比例与整体好坏客户比例相差越大，IV值越大，否则，IV值越小。
• IV值的取值范围是[0,+∞)，当分箱中只包含好客户或坏客户时，IV = +∞，当分箱中好坏客户比例等于整体好坏客户比例时，IV为0。

在评分卡建模流程中，WOE（Weight of Evidence）常用于特征变换，IV（Information Value）则用来衡量特征的预测能力。

WOE（Weight of Evidence）叫做证据权重，WOE在业务中常有哪些应用呢？

• 处理缺失值：当数据源没有100%覆盖时，那就会存在缺失值，此时可以把null单独作为一个分箱。这点在分数据源建模时非常有用，可以有效将覆盖率哪怕只有20%的数据源利用起来。
• 处理异常值：当数据中存在离群点时，可以把其通过分箱离散化处理，从而提高变量的鲁棒性（抗干扰能力）。例如，age若出现200这种异常值，可分入“age > 60”这个分箱里，排除影响。
• 业务解释性：我们习惯于线性判断变量的作用，当x越来越大，y就越来越大。但实际x与y之间经常存在着非线性关系，此时可经过WOE变换。

$$WOE_i = ln(\frac{Bad_i}{Bad_T}/\frac{Good_i}{Good_T}) = ln(\frac{Bad_i}{Bad_T})-ln(\frac{Good_i}{Good_T})$$

IV（Information Value）是与WOE密切相关的一个指标，常用来评估变量的预测能力。因而可用来快速筛选变量。在应用实践中，其评价标准如下：

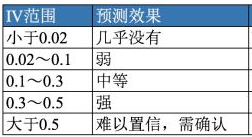
而IV的计算公式定义如下，其可认为是WOE的加权和：

$$IV_i = (\frac{Bad_i}{Bad_T}-\frac{Good_i}{Good_T}) * WOE_i$$

$$IV = \sum_{i=1}^{n}IV_i$$

基于stepwise的变量筛选

基于stepwise的变量筛选方法也是评分卡中变量筛选最常用的方法之一。具体包括三种筛选变量的方式：

• 前向选择forward：逐步将变量一个一个放入模型，并计算相应的指标，如果指标值符合条件，则保留，然后再放入下一个变量，直到没有符合条件的变量纳入或者所有的变量都可纳入模型。
• 后向选择backward：一开始将所有变量纳入模型，然后挨个移除不符合条件的变量，持续此过程，直到留下所有最优的变量为止。
• 逐步选择stepwise：该算法是向前选择和向后选择的结合，逐步放入最优的变量、移除最差的变量。

基于特征重要度的变量筛选

基于特征重要度的变量筛选方法是目前机器学习最热门的方法之一，其原理主要是通过随机森林和GBDT等集成模型选取特征的重要度。

基于LASSO正则化的变量筛选

L1正则化通常称为Lasso正则化，它是在代价函数上增加了一个L1范数。

随着机器学习的发展，变量选择的方法也在增加。信用风险模型中典型的变量选择方法：

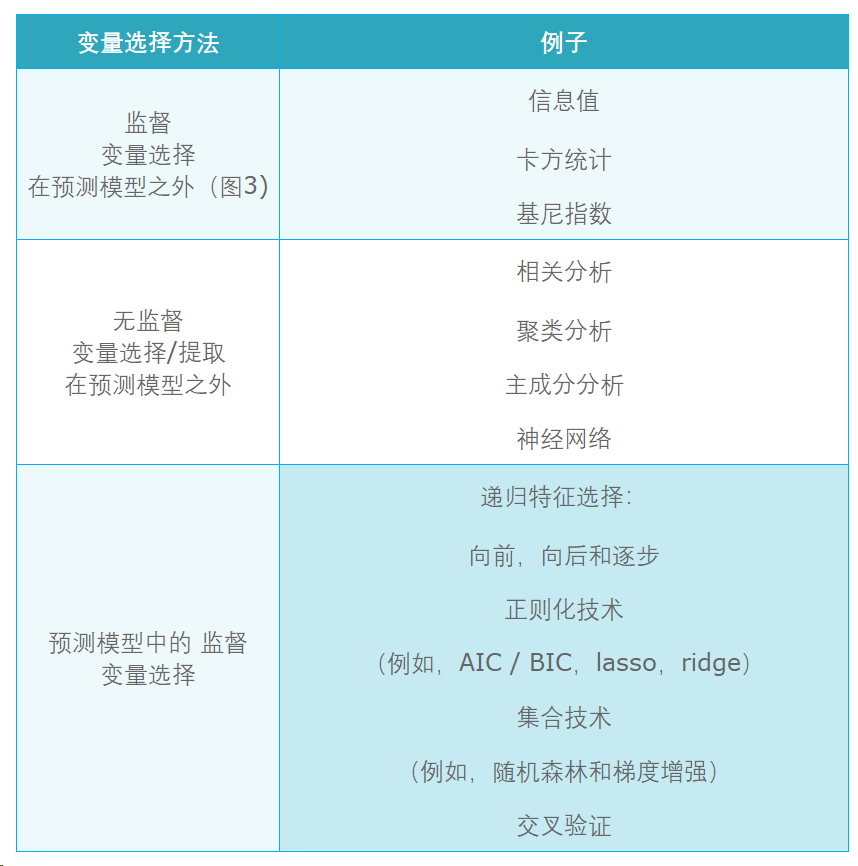
更多方法请参考： 机器学习之特征选择方法

变量相关性分析

常用分析方法：

• 变量两两相关性分析
• 变量的多重共线性分析

为什么要进行相关性分析？

设想建立一个具有两变量$X_1$和$X_2$的线性模型，真实模型是$Y=X_1+X_2$。如果$X_1$和$X_2$线性相关（比如说$X_1\approx 2X_2$），那么拟合模型$Y=3X_2$, $Y=2X_1-X_2$或$Y=51X_1-99X_2$的效果都一样好，理想状态下，系数权重会有无数种取法，使系数权重变得无法解释，导致变量的每个分段的得分也有无数种取法（后面我们会发现变量中不同分段的评分会用到变量的系数）。

当两个变量具有高相关性时，保留IV值大。

变量分箱

评分卡模型通过对变量进行分箱来实现变量的分段。那么什么是分箱呢？以下为分箱的定义：

• 对连续变量进行分段离散化
• 将多状态的离散变量进行合并，减少离散变量的状态数

常见的分箱类型有以下几种：

无监督分箱

• 等频分箱：把自变量按从小到大的顺序排列，根据自变量的个数等分为k部分，每部分作为一个分箱。
• 等距分箱：把自变量按从小到大的顺序排列，将自变量的取值范围分为k个等距的区间，每个区间作为一个分箱。
• 聚类分箱：用k-means聚类法将自变量聚为k类，但在聚类过程中需要保证分箱的有序性。

由于无监督分箱仅仅考虑了各个变量自身的数据结构，并没有考虑自变量与目标变量之间的关系，因此无监督分箱不一定会带来模型性能的提升。

有监督分箱

包括 Split 分箱和 Merge 分箱

• Split 分箱是一种自上而下(即基于分裂)的数据分段方法。Split 分箱和决策树比较相似，切分点的选择指标主要有 Entropy，Gini 指数和 IV 值等。
• Merge 分箱，是一种自底向上(即基于合并)的数据离散化方法。Merge 分箱常见的类型为Chimerge分箱。

ChiMerge 分箱

ChiMerge 分箱是目前最流行的分箱方式之一，其基本思想是如果两个相邻的区间具有类似的类分布，则这两个区间合并；否则，它们应保持分开。Chimerge通常采用卡方值来衡量两相邻区间的类分布情况。

ChiMerge的具体算法如下：

1. 输入：分箱的最大区间数n
2. 初始化

• 连续值按升序排列，离散值先转化为坏客户的比率，然后再按升序排列
• 为了减少计算量，对于状态数大于某一阈值 (建议为100) 的变量，利用等频分箱进行粗分箱
• 若有缺失值，则缺失值单独作为一个分箱

3. 合并区间

• 计算每一对相邻区间的卡方值
• 将卡方值最小的一对区间合并
• 重复以上两个步骤，直到分箱数量不大于n

4. 分箱后处理

• 对于坏客户比例为 0 或 1 的分箱进行合并 (一个分箱内不能全为好客户或者全为坏客户)。
• 对于分箱后某一箱样本占比超过 95% 的箱子进行删除。
• 检查缺失分箱的坏客户比例是否和非缺失分箱相等，如果相等，进行合并。

5. 输出：分箱后的数据和分箱区间。

总结一下特征分箱的优势：

• 特征分箱可以有效处理特征中的缺失值和异常值。
• 特征分箱后，数据和模型会更稳定。
• 特征分箱可以简化逻辑回归模型，降低模型过拟合的风险，提高模型的泛化能力。
• 将所有特征统一变换为类别型变量。
• 分箱后变量才可以使用标准的评分卡格式，即对不同的分段进行评分。

为了创建一个对过度拟合具有弹性的健壮模型，每个箱应该包含来自总账户的足够数量的观察结果（大多数从业者建议的最小值为5%），如果最大箱占据了总样本量的90%以上，那么弃用该变量。

WOE编码

在风控用到的数据里，我们会用到两种变量：

• Numerical Variable，数值变量。例如逾期金额，天数
• Categorical Variable，类别变量。例如客户职业

在制作评分卡过程中，我们还需要把数值变量变成类别变量，例如客户年龄段，我们可以划分为[20及以下],[21-30],[31-40],[41-50],[51-60],[61-70],[70以上]七个类别，这时候我们就把数值变成了类别。这种把数值变成类别的技巧叫做分箱（binning）。

但是当把所有变量都变成类别后，这时候你也许有这个疑惑：怎么去训练一个模型呢？例如逻辑回归，只能用数值作为特征输入。怎么把类别变成数值呢？

你这时候想到的可能是one-hot encoding，但还是有问题，对于逻辑回归来说，one-hot encoding输出的矩阵太稀疏了，很难让逻辑回归有很好的效果。这时候，我们可以试试把类别或者分箱转化成响应的数值。这个分数必须和必须有这个特性：分数越大，代表这个变量给bad label的贡献度越大，这个贡献度，视运算符号不同，可以是正向，也可以是负向，但我们期望它们之间有个线性关系。这时候我们需要引入WOE编码。

在变量筛选中对WOE已经有了简单的介绍。这里以实例进行介绍：

我们观察Bad Rate 和WOE的关系，可以看到WOE越大，Bad Rate越高，也就是说，通过WOE变换，特征值不仅仅代表一个分类，还代表了这个分类的权重。

对于类别变量进行WOE编码很好理解，为什么数值变量需要在分箱以后再进行WOE编码？分箱+WOE编码主要要解决的问题是把非线性的特征转化为线性。

例如在风控场景里，我们可能用到客户的年龄做特征。我们知道肯定不是年龄越大风险越高，或者年龄越大风险越低，一定是有个年龄段的风险是比其他年龄段高些。

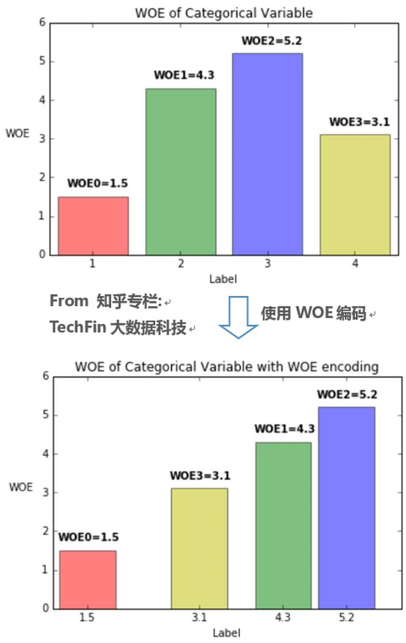
总结下WOE编码的优势：

• 可提升模型的预测效果
• 将自变量规范到同一尺度上
• WOE能反映自变量取值的贡献情况
• 有利于对变量的每个分箱进行评分
• 转化为连续变量之后，便于分析变量与变量之间的相关性
• 与独热向量编码相比，可以保证变量的完整性，同时避免稀疏矩阵和维度灾难

模型训练

Logistic回归是信用评分中用于解决二元分类问题的常用技术。逻辑回归通过sigmoid函数$ y = \frac{1}{1+e^{-z}}$ 将线性回归模型$z=\boldsymbol{w}^T\boldsymbol{x}+b$产生的预测值转换为一个接近0或1的拟合值：

$$h(x)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(\boldsymbol{w}^T\boldsymbol{x}+b)}}$$

上式的$h(x)$可视为事件发生的概率$p(y=1|\boldsymbol{x})$，变换后得到：$\ln\frac{p}{1-p}=z=\boldsymbol{w}^T\boldsymbol{x}+b$

其中，$p/(1-p)$为比率(odds)，即违约概率与正常概率的比值。$\ln{p/(1-p)}$为logit函数，即比率的自然对数。因此，逻辑回归实际上是用比率的自然对数作为因变量的线性回归模型。

在模型拟合之前，变量选择的再一次迭代对于检查新的WOE变换变量是否仍然是良好的模型候选变量是有价值的。优选的候选变量是具有较高信息值（通常在0.1和0.5之间）的变量，与因变量具有线性关系，在所有类别中具有良好的覆盖率，具有正态分布，包含显著的总体贡献，并且与业务相关。

由逻辑回归的基本原理，我们将客户违约的概率表示为p，则正常的概率为1-p。因此，可以得到：

$$Odds = \frac{p}{1-p}$$

此时，客户违约的概率p可表示为：

$$p = \frac{Odds}{1+Odds}$$

评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义，即可表示为下式：

$$Score = A – B\log(Odds)$$

其中，A和B是常数。式中的负号可以使得违约概率越低，得分越高。通常情况下，这是分值的理想变动方向，即高分值代表低风险，低分值代表高风险。 逻辑回归模型计算比率如下所示：

$$ log(Odds)=\beta _0 + \beta _1x_1+…+\beta _nx_n$$

其中，用建模参数拟合模型可以得到模型参数$\beta _0,\beta _1,…,\beta _n$。 式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下，需要设定两个假设：

• 给某个特定的比率设定特定的预期分值
• 确定比率翻番的分数（PDO） 根据以上的分析，我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值应该为P+PDO。

代入式中，可以得到如下两个等式：

$$P = A – B\log(x)$$

$$P – PDO = A – B\log(2x)$$

假设设定评分卡刻度使得比率为1:20（违约正常比）时的分值为50分，PDO为10分，代入式中求得：B=14.43，A=6.78 则分值的计算公式可表示为：

$$Score = 6.78 -14.43\log(Odds)$$

评分卡刻度参数A和B确定以后，就可以计算比率和违约概率，以及对应的分值了。通常将常数A称为补偿，常数B称为刻度。 则评分卡的分值可表达为：

$$Score = A – B\{\beta _0+\beta _1x_1+…+\beta _nx_n\}$$

式中：变量$x_1,…,x_n$是出现在最终模型中的自变量，即为入模指标。由于此时所有变量都用WOE转换进行了转换，可以将这些自变量中的每一个都写$(\beta _i\omega _{ij})\delta _{ij}$的形式：

$$Score = A-B\{\beta _0+(\beta _1\omega _{11})\delta _{11}+(\beta _1\omega _{12})\delta _{12}+…+(\beta _2\omega _{21})\delta _{21}+…\}$$

式中：

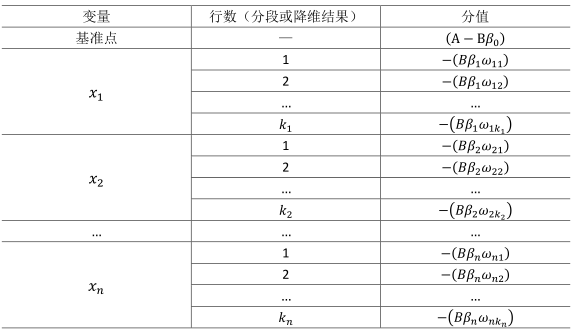
• $\omega _{ij}$为第i行第j个变量的WOE，为已知变量
• $\beta _i$为逻辑回归方程中的系数，为已知变量
• $\delta _{ij}$为二元变量，表示变量i是否取第j个值。

上式可重新表示为：

$$Score = (A-B\beta _0)-(B\beta _1\omega _{11})\delta _{11}-(B\beta _1\omega _12)\delta _{12}-…-(B\beta _x\omega _{x1}-…$$

此式即为最终评分卡公式。如果$x_1…x_n$变量取不同行并计算其WOE值，式中表示的标准评分卡格式，如表3.20所示：$(A-B\beta _0)$；由于分值分配公式中的负号，模型参数$\beta _0,\beta _1,…,\beta _n$也应该是负值；变量$x_i$的第j行的分值取决于以下三个数值：

拒绝推断

申请评分卡的模型开发过程中使用的数据实际上并不是从申请总体样本中随机选择的，而仅仅是从过去已经被接受的客户样本中选择的。因此，开发申请评分卡时将对被拒绝客户的状态进行推断并纳入模型开发数据集中，即拒绝推断过程。拒绝推断的常用方法包括：

• 简单赋值法：人为指定被拒绝账户的标签
  • 忽略被拒绝申请
  • 所有被拒申请赋值为违约标签
  • 按比例赋值，使得其坏客户率是通过样本的2~5倍以上
• 强化法：通过外推法确定拒绝账户的标签
  • 简单强化法：使用通过客户开发的模型对被拒绝客户评分，将其中低分段赋予违约标签。使得拒绝客户的坏客户率为通过的2~5倍以上
  • 模糊强化法：通过模型计算得到正常和违约概率。
  • 打包强化法：先用开发的评分卡对被拒客户评分，然后指定每个分值区间的违约客户数量。

模型表现

模型评估是模型构建过程的最后一步。它由三个不同的阶段组成：评估，验证和接受。

评估准确性 – 我是否构建了正确的模型？ – 是第一个要求测试模型的问题。评估的关键指标是统计测量，包括模型准确性，复杂性，错误率，模型拟合统计，变量统计，显著性值和优势比。

验证稳健性 – 我是否构建了正确的模型？ – 从分类准确性和统计评估转向排名能力和业务评估时，是下一个要问的问题。

验证度量的选择取决于模型分类器的类型。二元分类问题最常见的指标是增益图，提升图，ROC曲线和Kolmogorov-Smirnov图。ROC曲线是可视化模型性能的最常用工具。它是一个多用途工具，用于：

• 冠军挑战者选择最佳表现模式的方法
• 在看不见的数据上测试模型性能并将其与训练数据进行比较
• 选择最佳阈值，最大化真阳性率，同时最小化假阳性率

通过绘制灵敏度与不同阈值的误报概率（误报率）来创建ROC曲线。评估不同阈值下的性能指标是ROC曲线的理想特征。根据业务策略，不同类型的业务问题将具有不同的阈值。

ROC曲线下面积（AUC）是指示分类器预测能力的有用度量。在信用风险中，0.75或更高的AUC是行业认可的标准和模型验收的先决条件。

接受有用性 – 模型是否会被接受？ – 是最后一个问题，以便测试该模型是否对商业前景有价值。这是数据科学家必须将模型结果回放给业务并“捍卫”其模型的关键阶段。关键评估标准是模型的商业利益，因此，效益分析是呈现结果的核心部分。数据科学家应该尽一切努力以简洁的方式呈现结果，因此结果和发现很容易理解。如果不能实现这一点，可能会导致模型拒绝，从而导致项目失败。

模型一旦对齐，下一步就是将模型调整到业务所需的比例。这称为缩放。缩放作为一种测量工具，可以在不同的评分卡中提供分数的一致性和标准化。最低和最高分数值以及分数范围有助于风险解释，并应向业务部门报告。通常，业务要求是对多个评分卡使用相同的分数范围，因此它们都具有相同的风险解释。

信用风控策略

模型开发之后需要基于建模样本确定风控策略。一个好的风控策略应具备：

• 增加客户数量
• 减少风险损失
• 最大化利润

基于开发的评分卡，我们可以获得建模样本的审批决策表。结合审批决策表与损失或者利润目标，制定常用风控策略：

• 评分临界值：实现通过率、坏客户率、或利润损失率等业务目标
• 通过交叉决策矩阵实现风险定价，实现差异化的利率、额度等：
  • 风险评分与利润损失比
  • 风险评分与债务收入比
  • 风险评分与流失倾向评分

一个好的模型一般应具有以下特征：

• 在进行数据描述时变量应该有意义。通常，某些变在特定客群的不同风险模型中重复出现。例如，信用卡行为评分卡模型中，授信使用率经常出现；申请评分卡模型中收入水平、职业和历史信贷产品拥有情况比人口统计变量重要。
• 变量的预测力或贡献度，应该在模型的变量之间分布。
• 模型中不应该包含太多变量。通常，包含的变量不超过9~20个(最优10~12个)。变量太多可能导致过拟合，变量太少往往区分度不够。
• 最终模型的变量应该能够确保包含稳健一致的数据，并在后续实施阶段能够准确获取。

评分卡模型搭建实战

数据来源： Give Me Some Credit比赛

数据字段说明：

列名	字段说明
SeriousDlqin2yrs	两年内是否有严重违约（好坏用户判断）
RevolvingUtilizationOfUnsecuredLines	可用信贷额度比例，信用卡和个人信用额度（不动产和汽车贷款等分期付款债务除外）的总余额除以信用额度之和
age	借款人年龄
NumberOfTime30-59DaysPastDueNotWorse	两年内35-59天逾期次数
DebtRatio	借款人负债比率（每月债务支付、赡养费、生活费之和除以月收入）
MonthlyIncome	借款人月收入
NumberOfOpenCreditLinesAndLoans	开放式信贷和贷款数量
NumberOfTimes90DaysLate	两年内90天或高于90天逾期的次数
NumberRealEstateLoansOrLines	不动产贷款或额度数量
NumberOfTime60-89DaysPastDueNotWorse	两年内60-89天逾期次数
NumberOfDependents	借款人家属数量（不包括本人在内）

探索数据

import pandas as pd
from dataprep.eda import plot
import warnings
warnings.filterwarnings('ignore')

train_data = pd.read_csv('cs-training.csv', index_col=0)
train_data.columns = ['严重违约', '可用额度比例','年龄', '35-69天逾期次数', '负债比例','月收入','普通贷款数量','高于90天逾期次数','不动产贷款数量','60-89天逾期次数','家属数量']
train_data = train_data[['年龄','家属数量','月收入','负债比例','可用额度比例','普通贷款数量','不动产贷款数量','35-69天逾期次数','60-89天逾期次数','高于90天逾期次数','严重违约']]


# 手工探索数据
print(train_data.shape)
print(train_data.info())
print(train_data.isnull().sum())
print(train_data.describe().T)
print(train_data['严重违约'].value_counts())
print(train_data['严重违约'].sum()/train_data['严重违约'].count())

# 使用EDA工具探索数据
plot(train_data)

数据预处理

1）缺失值处理

常见方法：

• 直接删除含有缺失值的样本
• 根据样本之间的相似性填补缺失值
• 根据变量之间的相关关系填补缺失值

存在缺失的特征：月收入、家属人数

这里假设一个人的月收入和家属人数和自身的 其他个人特征有关联，这里根据变量之间的相关关系采用随机森林法填补。

from sklearn.ensemble import RandomForestRegressor

def fill_income_missing(data, to_fill):
    df = data.copy()
    columns = [*df.columns]
    columns.remove(to_fill)
    
    # 移除有缺失值的列
    columns.remove('家属数量')
    X = df.loc[:, columns]
    y = df.loc[:, to_fill]
    X_train = X.loc[df[to_fill].notnull()]
    y_train = y.loc[df[to_fill].notnull()]
    X_pred = X.loc[df[to_fill].isnull()]
    rfr = RandomForestRegressor(random_state=22, n_estimators=200, max_depth=3, n_jobs=-1)
    rfr.fit(X_train, y_train)
    y_pred = rfr.predict(X_pred).round()
    df.loc[df[to_fill].isnull(), to_fill] = y_pred
    return df

def fill_dependents_missing(data, to_fill):
    df = data.copy()
    columns = [*df.columns]
    columns.remove(to_fill)
    
    X = df.loc[:, columns]
    y = df.loc[:, to_fill]
    X_train = X.loc[df[to_fill].notnull()]
    y_train = y.loc[df[to_fill].notnull()]
    X_pred = X.loc[df[to_fill].isnull()]
    rfr = RandomForestRegressor(random_state=22, n_estimators=200, max_depth=3, n_jobs=-1)
    rfr.fit(X_train, y_train)
    y_pred = rfr.predict(X_pred).round()
    df.loc[df[to_fill].isnull(), to_fill] = y_pred
return df

train_data = fill_income_missing(train_data, '月收入')
train_data = fill_dependents_missing(train_data, '家属数量')
print(train_data.isnull().sum())

2) 异常值处理

a. 删除年龄为0的数据

train_data = train_data.loc[train_data['年龄'] > 0]

b. 去除逾期次数中的异常数据

import matplotlib.pyplot as plt

columns = ['35-69天逾期次数','60-89天逾期次数','高于90天逾期次数']
train_data.loc[:, columns].plot.box(vert=False)

train_data = train_data[(train_data['35-69天逾期次数'] < 90) & (train_data['60-89天逾期次数'] < 90)  & (train_data['高于90天逾期次数'] < 90)]

信用卡模型训练

这里直接使用 Scorecard-Bundle这个Python包进行训练。Scorecard-Bundle是一个基于Python的高级评分卡建模API，实施方便且符合Scikit-Learn的调用习惯，包含的类均遵守Scikit-Learn的fit-transform-predict习惯。Scorecard-Bundle包括基于ChiMerge的特征离散化、WOE编码、基于信息值（IV）和共线性的特征评估、基于逻辑回归的评分卡模型、以及针对二元分类任务的模型评估。

1） 特征离散化（ChiMerge）

from scorecardbundle.feature_discretization import ChiMerge as cm
from scorecardbundle.feature_discretization import FeatureIntervalAdjustment as fia
from scorecardbundle.feature_encoding import WOE as woe
from scorecardbundle.feature_selection import FeatureSelection as fs
from scorecardbundle.model_training import LogisticRegressionScoreCard as lrsc
from scorecardbundle.model_evaluation import ModelEvaluation as me

X = train_data.iloc[:, :-1]
y = train_data.iloc[:, -1]

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0, test_size=0.25)

trans_cm = cm.ChiMerge(max_intervals=10, min_intervals=5, output_dataframe=True)
result_cm = trans_cm.fit_transform(X_train, y_train) 
print(trans_cm.boundaries_) # 每个特征的区间切分

2） 特征编码（WOE）和评估（IV）

trans_woe = woe.WOE_Encoder(output_dataframe=True)
result_woe = trans_woe.fit_transform(result_cm, y_train)
print(trans_woe.iv_) # 每个特征的信息值 (iv)
print(trans_woe.result_dict_) # 每个特征的WOE字典和信息值 (iv)

3) 手动调整分箱

观察每一个特征的分布和响应率，确定分箱是否合理，如果不合理就需要人工设置边界。

col = '年龄'
fia.plot_event_dist(result_cm[col],y_train,x_rotation=60)
new_x = cm.assign_interval_str(X_train[col].values,[22, 33, 43, 53, 62, 67, 74]) # apply new interval boundaries to the feature
woe.woe_vector(new_x, y_train.values) # check the information value of the resulted feature that applied the new intervals
fia.plot_event_dist(new_x,y_train, x_label=col,x_rotation=60)

feature_list = []
result_cm[col] = new_x # great explainability and predictability. Select.
feature_list.append(col)
print(feature_list)

4) WOE编码

完成全部特征的分组检查后，再次将分组特征进行WOE编码

trans_woe = woe.WOE_Encoder(output_dataframe=True)
result_woe = trans_woe.fit_transform(result_cm[feature_list], y_train) 
print(result_woe.head())
print(trans_woe.iv_)

5) 特征选择

剔除预测力过低（通常用IV不足0.02筛选）、以及相关性过高引起共线性问题的特征。(相关性过高的阈值默认为皮尔森相关性系数大于0.6，可通过threshold_corr参数调整)

fs.selection_with_iv_corr(trans_woe, result_woe) # corr_with 列示了与该特征相关性过高的特征和相关系数

6) 模型训练

model = lrsc.LogisticRegressionScoreCard(trans_woe, PDO=-20, basePoints=100, verbose=True)
model.fit(result_woe, y_train)
print(model.woe_df_) # 从woe_df_属性中可得评分卡规则

7) 模型校验

sc_table = model.woe_df_.copy()
result = model.predict(X_train[feature_list], load_scorecard=sc_table) # Scorecard should be applied on the original feature values
result_test = model.predict(X_test[feature_list], load_scorecard=sc_table) # Scorecard should be applied on the original feature values
result.head() # if model object's verbose parameter is set to False, predict will only return Total scores

# Train
evaluation = me.BinaryTargets(y_train, result['TotalScore'])
evaluation.plot_all()
  
# Validation
evaluation = me.BinaryTargets(y_test, result_test['TotalScore'])
evaluation.plot_all()

模型相关数据：

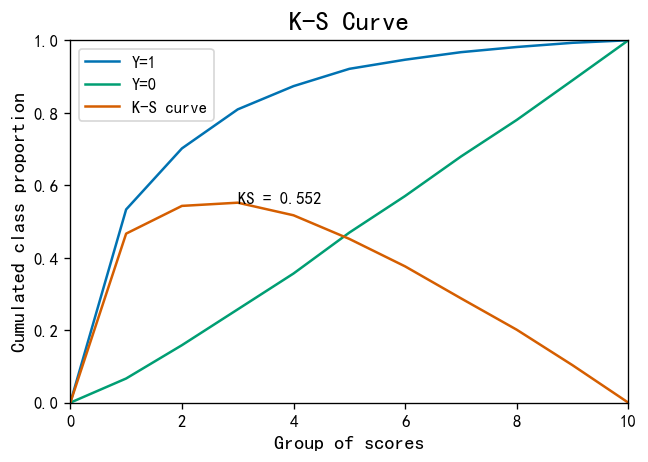
KS指标: 用以评估模型对好、坏客户的判别区分能力，计算累计坏客户与累计好客户百分比的最大差距。KS值范围在0%-100%，判别标准如下：

• KS: <20% : 差
• KS: 20%-40% : 一般
• KS: 41%-50% : 好
• KS: 51%-75% : 非常好
• KS: >75% : 过高，需要谨慎的验证模型

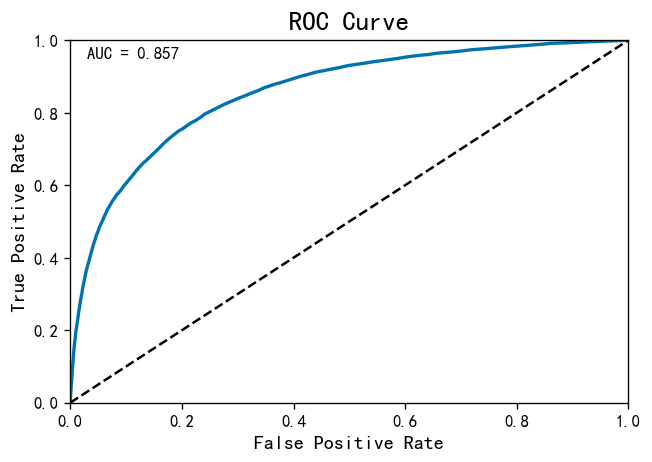
ROC曲线就越往左上方靠拢，它下面的面积(AUC)也就越大：

• 如果AUC的值达到80，那说明分类器分类非常准确
• 如果AUC值在60～0.80之间，那分类器有优化空间，可以通过调节参数得到更好的性能
• 如果AUC值小于60，那说明分类器模型效果比较差

参考链接：

• 信用评分卡模型开发与应用
• R语言评分卡模型（公开版）
• 手把手教你搭建评分卡模型