使用Excel搭建推荐系统

在上一篇 重新认识Excel的文章中，提到了Excel无所不能，然后就想到了曾经看到的这篇关于如何使用Excel搭建推荐引擎的文章。于是找了出来做了下简单的翻译（只翻译了重点部分）。

在互联网上有无限的货架空间，找到你想看的东西可能会让人筋疲力尽。幸运的是，与决策疲劳作斗争是 Netflix 的工作……而且他们很擅长。太擅长了。他们神奇地向您推荐完美的电影，这样您的眼睛就会一直盯着管子，他们会把您的拖延变成周末沙发上的狂欢。该死的，Netflix。你的秘诀是什么？你怎么这么了解我们？“魔法”非常简单，本教程使用分步电子表格揭示了其中的秘密。

尽管自Netflix Prize 竞赛以来有大量关于推荐系统的论文或视频，但大多数要么 (A) 技术太高，初学者无法使用，要么 (B) 水平太高，不实用。

在这篇文章中，我们将从头开始构建一个电影推荐系统，其中包含简单的英语解释和可以在 Excel 中遵循的分步公式。所有梯度下降推导都是手工计算的，您可以使用 Excel 下拉过滤器来微调模型的超参数并增强您的理解。

学习内容

• 构建帮助赢得 100 万美元 Netflix 奖金的算法版本 SVD++ 背后的确切步骤。
• 机器如何实际学习（梯度下降）。即使您从未告诉过 Netflix，也可以观看 Netflix 了解您的电影品味。
• 超参数调优。了解如何调整模型输入 （学习率、L2 正则化、# of epochs、权重初始化）以获得更好的预测。
• 模型评估和可视化。了解训练数据和测试数据之间的区别，如何防止过度拟合，并了解如何可视化模型的特征。

在简要介绍了推荐系统之后，我将通过以下 4 个部分来构建一个模型来预测少数好莱坞明星的电影评分。

• 第一部分：模型概览
• 第二部分：观看魔法秀（权重初始化和训练）
• 第三部分：魔法揭秘（梯度下降、导数）。我将逐步讲解机器学习魔法背后的数学，我将使用实数作为例子代入批量梯度下降的公式（不会使用“宏”或者Excel求解器之类的东西隐藏细节）。
• 第四部分：模型评估和可视化

推荐系统简介

电影推荐系统可以简化为两大类：协同过滤（询问密友）和基于内容的过滤（标签匹配）

协同过滤

协同过滤基于类似行为进行推荐。

如果Ross和Rachel过去喜欢类似的东西，那么我们将Rachel喜欢而Ross没看过的电影向Ross推荐。你可以将他们看成是“协同”过滤网络货架上的噪音的“品味分身”。如果两个用户的评分有强相关性，那么我们就认定这两个用户“相似”。评分可以是隐式的，也可以是显式的：

• 隐式（Binging）—— 整个周末，Ross和Rachel都沉溺于老剧《老友记》。尽管他们没人点赞，但我们相当确定他们喜欢《老友记》（以及他们可能有点自恋）。
• 显式（喜欢）—— Ross和Rachel都点了赞。

协同过滤有两种：近邻方法和潜因子模型（矩阵分解的一种形式）。本文将聚焦一种称为 SVD++的潜因子模型。

基于内容的过滤

基于你过去喜欢的内容的明确标签（类型、演员，等等），Netflix向你推荐具有类似标签的新内容。

100 万美元的赢家

当数据集足够大时，协同过滤（CF）是电影推荐器中的不二之选。

虽然这两个大类之间有无数的混合和变化，但出人意料的是，当CF模型足够好时，加上元数据并没有帮助。这是为什么呢？人会说谎，行动不会。让数据自己说话。人们所说的他们喜欢的东西（用户偏好、调查等）与他们的行为之间存在很大差距。最好让人们的观看行为自己说话。窍门：想要改善Netflix推荐？访问 /WiViewingActivity清理你的观看记录，移除你不喜欢的项。）

2009年，Netflix奖励了一队研究人员一百万美元，这个团队开发了一个算法，将Netflix的预测精确度提升了10%. 尽管获胜算法实际上是超过100种算法的集成，SVD++（一种协同过滤算法）是其中最关键的算法之一，贡献了大多数收益，目前仍在生产环境中使用。

我们将创建的SVD++模型（奇异值分解逼近）和Simon Funk的博客文章中提到差不多。这篇不出名的文章是2006年Simon在Netflix竞赛开始时写的，首次提出了SVD++模型。在SVD++模型成功之后，几乎所有的Netflix竞赛参加者都用它。

SVD++ 关键思想

• “奇异值”（电影评分）可以“分解”或由一组隐藏的潜在因素（用户偏好和电影特征）决定，这些潜在因素直观地代表了类型、演员等。
• 潜在因素可以使用梯度下降和已知的电影评分迭代学习。
• 用户/电影偏见会影响某人的评分，并且也会被学习。

简单，但功能强大。让我们深入挖掘。

第一部分：模型概览

数据

博客文章模型使用 30 个虚构评分（5 个用户 x 6 部电影）来简化教程。要在我们进行过程中跟随并试验模型，您可以在 此处下载电子表格（Excel 或 Google 表格） 。

拆分数据——训练集和测试集

我们将使用25项评价来训练模型，剩下5项评价测试模型的精确度。

我们的目标是创建一个在25项已知评价（训练数据）上表现良好的系统，并希望它在5项隐藏（但已知）评价（测试数据）上做出良好的预测。

如果我们有更多数据，我们本可以将数据分为3组——训练集（约70%）、验证集（约20%）、测试集（约10%）。

评价预测公式

评价预测是用户/电影特征的矩阵乘法（“点积”）加上用户偏置，再加上电影偏置。

公式为：

$$\hat{r}_{i,j}=((u_1 m_1)+(u_2 m_2)+(u_3 m_3)+u_{bias}+m_{bias})$$

其中：

• $\hat{r}_{i,j}$表示用户i对电影j的预测评价
• $u_1$、$u_2$、$u_3$为用户潜因子
• $m_1$、$m_2$、$m_3$为电影潜因子
• $u_{bias}$为用户偏置
• $m_{bias}$为电影偏置

用户/电影特征

• 直觉上说，这些特征表示类型、演员、片长、导演、年代等因素。尽管我们并不清楚每项特征代表什么，但是当我们将其可视化后（见第四部分）我们可以凭直觉猜测它们可能代表什么。
• 出于简单性，我使用了3项特征，但实际的模型可能有50、100乃至更多特征。特征过多时，模型将“过拟合/记忆”你的训练数据，难以很好地推广到测试数据的预测上。
• 如果用户的第1项特征（让我们假定它表示“喜剧”）值较高，同时电影的“喜剧”特征的值也很高，那么电影的评价会比较高。

用户/电影偏置

用户偏置取决于评价标准的宽严程度。如果Netflix上所有的平均评分是3.5，而你的所有评分的均值是4.0，那么你的偏置是0.5. 电影偏置同理。如果《泰坦尼克号》的所有用户的评分均值为4.25，那么它的偏置是0.75（= 4.25 – 3.50）。

RMSE —— 评估预测精确度

RMSE = Root Mean Squared Error （均方根误差）

RMSE是一个数字，尝试回答以下问题“平均而言，预测评价和实际平均差了几颗星（1-5）？”

RMSE越低，意味着预测越准……

观察：

• 我们只在意绝对值差异。相比实际评分高估了1分的预测，和相比实际评分低估了1分的预测，误差相等，均为1。
• RMSE是误差同数量级的平均，而不是误差绝对值的平均。在我们上面的例子中，误差绝对值的平均是75（1 + 1 + 0.25 = 2.25，2.25 / 3 = 0.75），但RMSE是0.8292. RMSE给较大的误差更高的权重，这很有用，因为我们更不希望有较大的误差。

超参数调整

通过电子表格的下拉过滤器，可以调整模型的3个超参数。你应该测试下每种超参数，看看它们对误差的影响。

• 训练epoch数—— 1个epoch意味着整个训练集都过了一遍
• 学习率—— 控制调整权重/偏置的速度
• L2（lambda）惩罚因子—— 帮助模型预防过拟合训练数据，以更好地概括未见测试数据。

现在，让我们看一场魔法秀，看看模型是如何从随机权重开始，学习最优权重的。

第二部分：观看魔法秀（权重初始化和训练）

观看梯度下降的实际操作感觉就像您在观看 David Blaine 的魔术。

• 他到底是怎么知道我会在52张牌中选这张的呢？
• 等等，他刚刚是不是浮空了？

最后你深感敬畏，想要知道魔术是如何变的。我会分两步演示，接着揭露魔法背后的数学。

抽一张卡，随便抽一张（权重初始化）

在训练开始，用户/电影特征的权重是随机分配的，接着算法在训练中学习最佳的权重。

为了揭示这看起来有多么“疯狂”，我们可以随机猜测数字，然后让计算机学习最佳数字。下面是两种权重初始化方案的比较：

• 简单—— 用户特征我随机选择了1、0.2、0.3，剩下的特征都分配0.1.
• Kaiming He—— 更正式、更好的初始化方法，从高斯分布（“钟形曲线”）中随机抽样作为权重，高斯分布的均值为零，标准差由特征个数决定（细节见后）。

观赏魔术（查看训练误差）

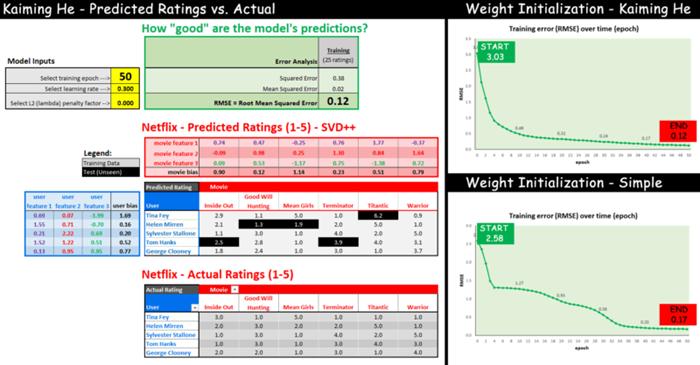
看看使用以上两种方案学习权重最佳值的效果，从开始（epoch 0）到结束（epoch 50），RMSE训练误差是如何变化的：

如你所见，两种权重初始化方法在训练结束时都会收敛到类似的“误差”（0.12 与 0.17），但“  Kaiming He”方法更快地收敛到较低的误差。

关键要点：无论我们从哪个权重开始，机器都会随着时间的推移学习到好的值！

注意：如果你想要试验其他初始化权重，可以在电子表格的“hyperparameters_and_initial_wts”表的G3-J7、N3-Q8单元格中输入你自己的值。权重取值范围为-1到1.

想要了解更多关于Kaiming He初始化的内容，请接着读下去；否则，可以直接跳到第3部分学习算法的数学。

Kaiming He权重初始化

权重 = 正态分布随机抽样，分布均值为0，标准差为 (=SquareRoot(2/# of features))

电子表格中的值由以下公式得到：=NORMINV(RAND(),0,SQRT(2/3))

$$W_l \sim \mathcal{N}(0, \sqrt{\frac{2}{n_l}}) \text{and} \mathbf{b}=0$$

第三部分：魔法揭秘

现在，是时候书呆一点，一步一步地了解梯度下降的数学了。如果你不是真想知道魔法是如何起效的，那么可以跳过这一部分，直接看第4部分。

梯度下降是在训练时使用的迭代算法，通过梯度下降更新电影特征、用户偏好的权重和偏置，以做出更好的预测。

梯度下降的一般周期为：

• 第 1 步 – 定义成本/损失函数以最小化和初始化权重
• 第 2 步 — 计算预测
• 第 3 步 – 计算梯度（相对于每个权重的成本变化）
• 第 4 步——在最小化成本的方向上更新每个权重“一点点地”（学习率）
• 第 5 步 — 重复第 2-4 步

你可以访问电子表格的“training”（训练）表，其中第11-16行是更新Tina Fey的第一项用户特征的过程。

由于数据集很小，我们将使用批量梯度下降。这意味着我们在训练时将使用整个数据集（在我们的例子中，一个用户的所有电影），而不是像随机梯度下降之类的算法一样每次迭代一个样本（在我们的例子中，一个用户的一部电影），当数据集较大时，随机梯度下降更快。

定义最小化的代价函数

我们将使用下面的公式，我们的目标是找到合适的潜因子（矩阵U、M）的值，以最小化SSE（平方误差之和）加上一个帮助模型提升概括性的L2权重惩罚项。

下面是Excel中的代价函数计算。计算过程忽略了1/2系数，因为它们仅用于梯度下降以简化计算。

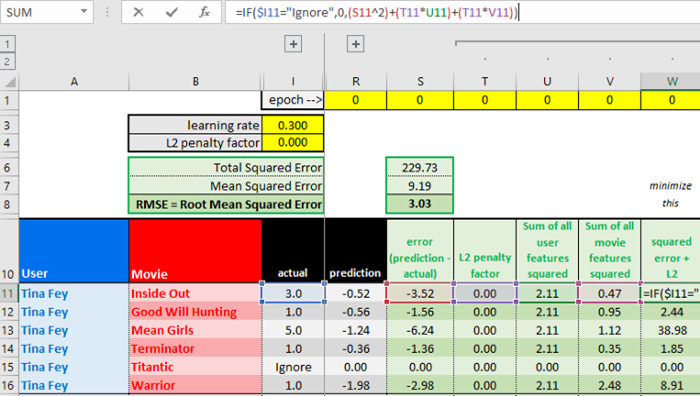
L2正则化和过拟合

我们加入了权重惩罚（L2正则化或“岭回归”）以防止潜因子值过高。这确保模型没有“过拟合”（也就是记忆）训练数据，否则模型在未见的测试电影上表现不会好。

之前，我们没有使用L2正则化惩罚（系数为0）的情况下训练模型，50个epoch后，RMSE训练误差为0.12.

但是模型在测试数据上的表现如何呢？

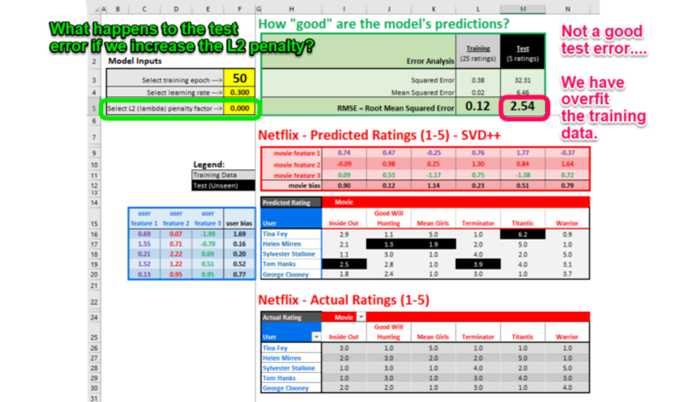
如果我们将 L2 惩罚因子从 0.000 更改为 0.300，我们的模型应该可以更好地概括未见过的测试数据：

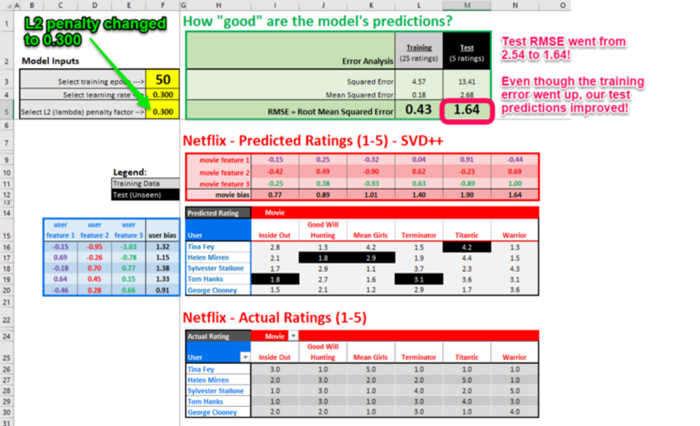
计算预测

我们将计算Tina的电影预测。我们将忽略《泰坦尼克号》，因为它在测试数据集中，不在训练数据集中。

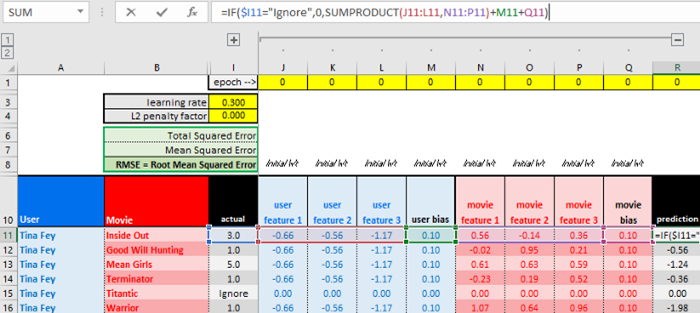
计算梯度

目标是找到误差对应于将更新的权重的梯度（“坡度”）。

得出梯度之后，稍微将权重“移动一点点”，沿着梯度的反方向“下降”，在对每个权重进行这一操作后，下一epoch的代价应该会低一些。

“移动一点点”具体移动多少，取决于学习率。在得到梯度（3.3）之后，会用到学习率。

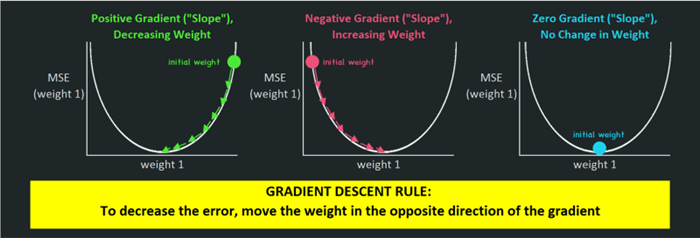
梯度下降法则：将权重往梯度的反方向移动，以减少误差

第1步：计算Tina Fey的第一个潜因子的代价梯度（$u_1$）

1.1整理代价目标函数，取代价在Tina Fey的第一个潜因子（$u_1$）上的偏导数。

$$\frac{\partial J(cost)}{\partial u_1}=\frac{1}{2} \sum_{(i, j): r(i,)=1}(\hat{r}_{i, j}-r_{i, j})^2+\frac{1}{2} \lambda(\sum_i\left\|u_i\right\|^2+\sum_j\left\|m_j\right\|^2)$$

1.2整理预测评价函数，改写为用户潜因子的平方和加上电影潜因子的平方和

$$\frac{\partial J}{\partial u_1}=\frac{1}{2} \sum(((u_1 m_1)+(u_2 m_2)+(u_3 m_3)+u_{bias }+m_{bias})-r_{i, j})^2+ \frac{1}{2} \lambda \sum(u_1^2+u_2^2+u_3^2)+\frac{1}{2} \lambda \sum (m_1^2+m_2^2+m_3^2)$$

1.3将公式每部分中的$u_1$视为常数，取$u_1$在公式每部分的代价上的偏导数。

1.3.1（Part 1 of 3）应用“链式法则”以得到偏导数。链式法则意味着我们将((外层函数的导数)*内层函数)* (内部函数的导数)

外层函数的导数：

$$\begin{gathered}=\frac{1}{2} \sum(((u_1 m_1)+(u_2 m_2)+(u_3 m_3)+u_{bias}+m_{bias})-r_{i, j})^2 \leftarrow \text { power rule} \\=2 \times \frac{1}{2}(((u_1 m_1)+(u_2 m_2)+(u_3 m_3)+u_{bias}+m_{bias})-r_{i, j})^1 \\=\text { (predicted rating }-\text { actual rating }) \\=(\text { error })\end{gathered}$$

内层函数的导数：

$$\begin{gathered}=\frac{1}{2} \sum((u_1 m_1)+(u_2 m_2)+(u_3 m_3)+u_{bias}+m_{bias})-r_{i, j} \leftarrow \text {constant rule} \\ ((u_1 m_1)+(0)+(0)+0+0)-0 \\ =m_1 \\ 1.3.1=(\text{error} x m_1)\end{gathered}$$

1.3.1（Part 2 of 3）应用“幂法则”以得到偏导数。根据幂法则，指数为2，所以将指数降1，并乘上系数1/2. $u_2$和$u_3$视作常数，变为0.

$$\begin{gathered}=\frac{1}{2} \lambda \sum(u_1^2+u_2^2+u_3^2) \\=2 \times \frac{1}{2} \times \lambda(u_1^1+0+0) \\=\lambda \times u_1 \\1.3 .2= (\lambda \times u_1)\end{gathered}$$

1.3.3 (Part 3 of 3 ) 应用“常数法则”以得到偏导数。

$$\begin{gathered}=\frac{1}{2} \lambda \sum(m_1^2+m_2^2+m_3^2) \\=0\end{gathered}$$

由于$u_1$对这些项毫无影响，结果是0。

$$1.3.3 =0$$

1.4 结合1.3.1、1.3.2、1.3.3得到代价在$u_1$上的偏导数。

$$\begin{aligned} \quad \text { Part } 1+\text { Part } 2+\text { Part } 3 \\ \frac{\partial J}{\partial u_1} &=(\text { error } x m_1)+(\lambda \times u_1)+0 \\ &=(\text { error } x m_1)+(\lambda \times u_1)\end{aligned}$$

第2步：对训练集中Tina看过的每部电影，利用前面的公式计算梯度，接着计算Tina看过的所有电影的平均梯度。

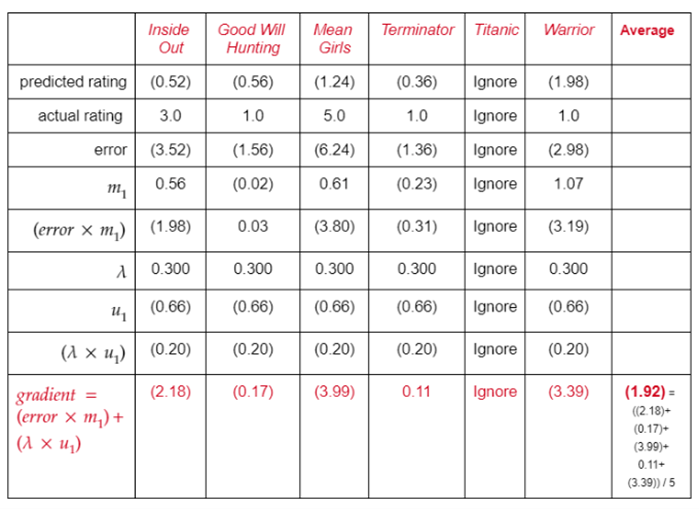
更新权重

学习Tina的旧$u_1$，学习率($\alpha$)，以及上面计算的平均梯度，更新$u_1$。我们将使用的学习率为0.3。

Gradient descent formula:

$$New \ u_1= old \ u_1-\alpha (average \ gradient)$$

$$New \ u_1=(0.66)-0.3(1.92)$$

$$New \ u_1=(0.66)+0.58$$

$$New \ u_1=(0.08)$$

“training”（训练）表的X11-X16单元格对应上面的计算过程。

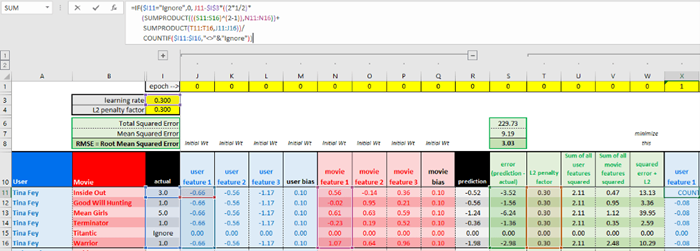
你可以看到，电影特征和用户/电影偏置以类似的方式更新。

每一个训练epoch更新所有的电影/用户特征及偏置。

第四部分：模型评估和可视化

现在我们已经训练好了模型，让我们可视化电影的2个潜因子。

如果我们的模型更复杂，包括10、20、50+潜因子，我们可以使用一种称为“ 主成分分析（PCA）”的技术提取出最重要的特征，接着将其可视化。

相反，我们的模型仅仅包括3项特征，所以我们将可视化其中的2项特征，基于学习到的特征将每部电影绘制在图像上。绘制图像之后，我们可以解释每项特征“可能代表什么”。

从直觉出发，电影特征1可能解释为悲剧与喜剧，而电影特征3可能解释为男性向与女性向。

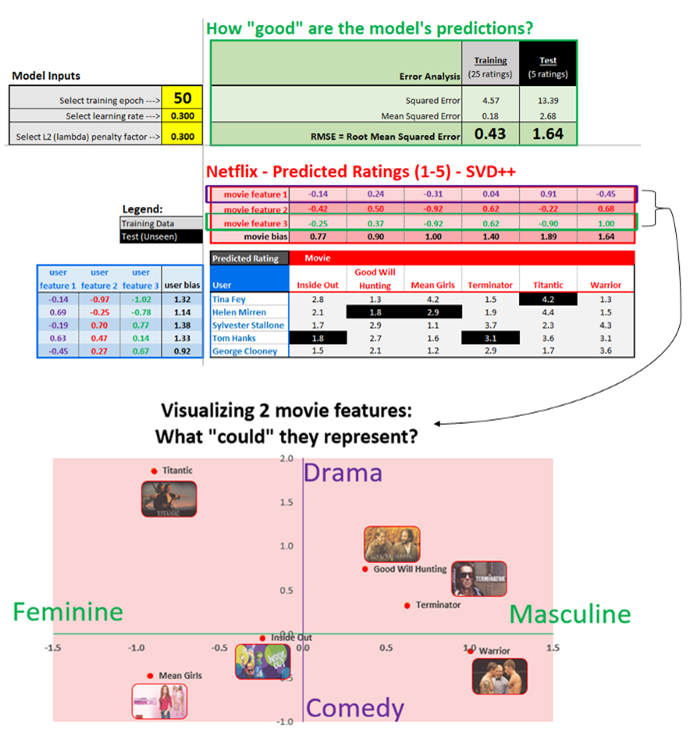
这不是完美的解释，但还算一种合理的解释。《勇士》（warrior）一般归为剧情片，而不是喜剧片。不过其他电影基本符合以上解释。

总结

电影评价由一个电影向量和一个用户向量组成。在你评价了一些电影之后（显式或隐式），推荐系统将利用群体的智慧和你的评价预测你可能喜欢的其他电影。向量（或“潜因子”）的维度取决于数据集的大小，可以通过试错法确定。

我鼓励你实际操作下电子表格，看看改变模型的超参数会带来什么改变。

参考链接：

• Netflix and Chill: Building a Recommendation System in Excel