百度百科的不靠谱说法

不妨先看看 百度百科 给出的费马原理的定义：光波在两点之间传递时，自动选取费时最少的路径。这是一种很常见的错误表述，只要看下面这个平面镜反射的例子就知道了。

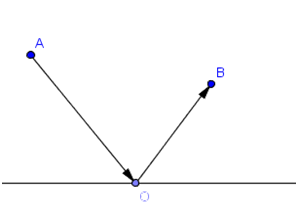
从A发出的光线，经过平面镜的反射到达B点，这条光线必然是可以真实存在的。可是这是光程最短的路径吗？显然不是，从A发出直接到达B的光线光程更短。所以使用“最小”一词是绝对错误的，费马原理其实是个局域性的原理，所有诸如最小的词均应当替换为极小。只要光程取极小值，无论是否是最小，它都是真实存在的光线。

用“极值”表述正确吗

那如果费马原理表述成：过两个定点的光总走光程极小的路径，是不是就正确了呢？其实这仍是一种错误的表述。光程取极小值只是一种常见情形，也存在其他情形。

首先举一个光程是定值的例子，如下图的椭圆形反射镜。

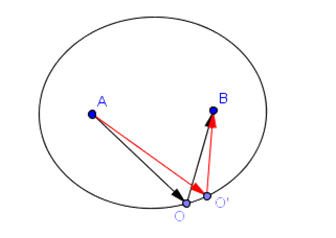
从椭圆的一个焦点A出发的光线，经过椭圆形镜子上任意一点的反射，一定会汇聚到另一个焦点B。这是因为椭圆的数学性质保证了这样光线的反射角一定等于入射角。在这个例子当中，任何一条真实光线都不是极小值了，因为不管反射点是椭圆上的哪个点，光程都是定值（是椭圆的定义：到两定点的距离之和为常值的点的轨迹）。

再举一个光程取极大值的例子，如下图：

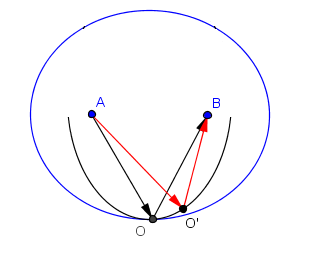
图中A、B是蓝色椭圆的两个焦点，在椭圆内任取一条黑色曲线为镜面。假设椭圆对称轴上的O点为黑色曲线和蓝色椭圆的切点。根据椭圆的性质，我们可以知道过O点的黑色光线确为真实光线。而在镜面上随意选取O’作为反射点形成的红色光线，则比黑色光线光程更短（只要记得椭圆的定义并注意到黑色曲线在椭圆内部即可知道这一点）。然而红色光线却并不满足反射角等于入射角，也就说它并非真实的光线。因此在这个例子中，光选取的路径实际上取了极大值。

什么是最正确的表述

那如果费马原理表述成：过两个定点的光总走光程为极大值、极小值或者定值的路径，是不是就正确了呢？这是物理专业课本中的表述，但仍然不够准确。仍以上图为例，说黑色光线取了极大值，其实是不准确的。因为只要本该是直线的光线稍微一弯曲，光程就会变得更长，从这个角度来讲，这又是一种极小值了。所以单说它是极大值还是极小值都不够准确。理解这种既极大又极小的函数也很简单，看看双曲抛物面的形状就可以了

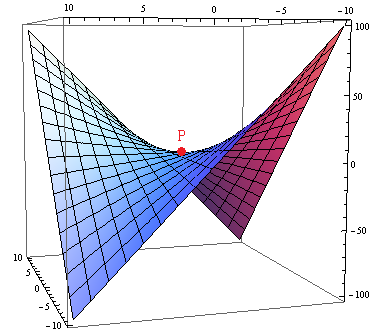
上图的P点，就既是极大值点又是极小值点（也可以说它二者都不是）。而费马原理中的光程，往往和这种情形类似。

因此如果把以上种种情形都考虑进去的话，费马原理将被叙述得很长。但其实在数学上有一种表述方法既准确又精炼，那就是：过两个定点的光总走光程的一阶变分为零的路径。

至于什么是变分，可以做如下理解：变分之于泛函，就相当于微分之于函数。而泛函则是函数的函数（以函数为自变量的特殊的函数），因为光线的路径本身是函数，而光程又是路径这个函数的函数，因此光程是泛函。所谓一阶变分为零，其实就和一阶导数为零意思相近。这种表述就自动包括了取极小值、极大值、定值、拐点这些种种情况了。

最后，为了更加严谨，突出费马原理的充分必要性，其实费马原理的最准确表述应该是：过两个定点的光走且仅走光程的一阶变分为零的路径。

费马原理最早由费马在1660年提出，阐述了光沿着所需时间为平稳的路径传播这一重要事实。但现在由于表述的不严谨，让人们对它的理解出现了很多偏差。

“我发现了一个美妙的证明，但由于空白太小而没有写下来。”——谨以此文纪念伟大的业余数学家之王——皮埃尔•德•费马。