算出过桥米线中肉片的加热时间
最近关于吃过桥米线中的猪肉可能会得旋毛虫病的问题,在网上引起了广泛讨论。这一次,死理性派就这个问题做了一次有趣的计算,从物理的角度来说说肉片的加热过程。讨论的关键在于肉片放到热汤里面之后,需要多长时间,肉片的中心才能达到灭杀旋毛虫幼虫所需的温度。
肉片在汤中的热传导模型
首先让我们来合理地简化一些条件。由于汤很多(一大碗),所以肉片的大小对于汤温的影响可以忽略不计。肉片的厚度才是更关键的因素。而肉片若非叠在一起,则两面都是和汤完全接触的,因此我们可以把肉片在汤中加热的过程看成一个一维的热传导问题。
诚然,肉片的厚度可能会不均匀,肉片在汤里面也可能有弯折。这都会对肉片中心的温度都会造成影响,但是为了得到一个初步的结论,不妨先不考虑这些次要因素。如此一来,我们就得到了一个单纯的一维热传导模型。在肉片放入汤中的时候,整个体系的温度如下图所示:
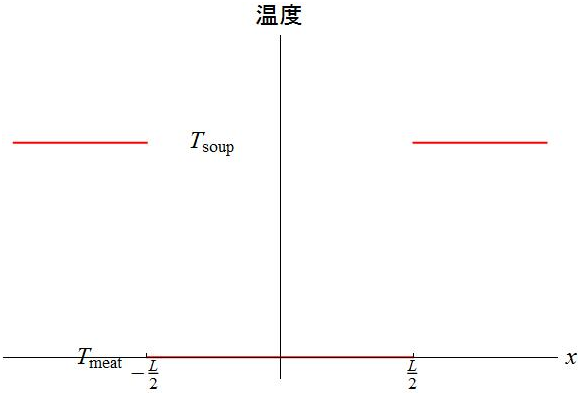
这里我们把坐标 x 的原点定在肉片的中心,设肉片的厚度为 L,则肉片即从 x = -L/2 到 L/2 的部分。可以确定出边界条件:设汤的温度恒定为 T soup 不变,肉的温度在开始时( t = 0 时) 为 T meat 。现在我们要做的,就是利用物理和数学的方法去求解这个体系里面的一维热传导方程[1]:
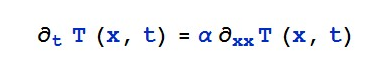
其中,α是肉片里面的热扩散系数,数值越大说明热在物体里面越容易传播,我们可以用水的热扩散系数来代替,即 α = 1.4 × 10 -7 m 2 /s[2](对于这个代替的合理性,在文末有详细的讨论)。解上面这个方程,具体的求解过程我们在这里略过不提(详细过程附件可见), 对于任意的 T soup 和 T meat 我们可以得到如下的解:
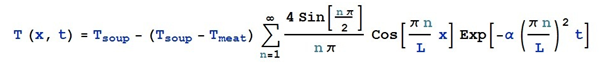
根据这个解,如果知道汤和肉片的初始温度以及肉的厚度,我们就可以给出肉内部温度随时间变化的曲线。如果以汤的最低温度 80℃,肉的初始温度是 0℃ (不妨就设肉品刚刚解冻),肉的厚度是1毫米为初始条件,那么我们可以画出当时间 t 为 0 秒, 1 秒, 2 秒, 3 秒的时候肉内部的温度的变化图:
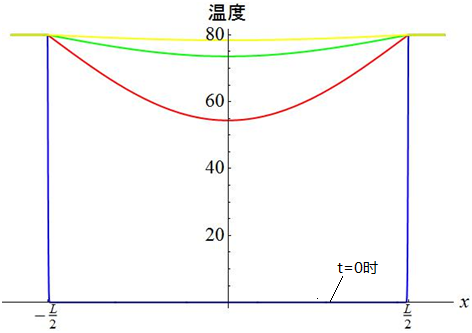
根据上图,3 秒之后肉片中心温度大约是 78℃,基本接近汤的温度了。
另一方面,我们也可以画出肉片中心的温度随时间变化的曲线,如下图所示,从左到右依次为厚度为 1 毫米、 2 毫米和 10 毫米的肉片,汤的温度是 80℃,肉片开始时是 0℃。
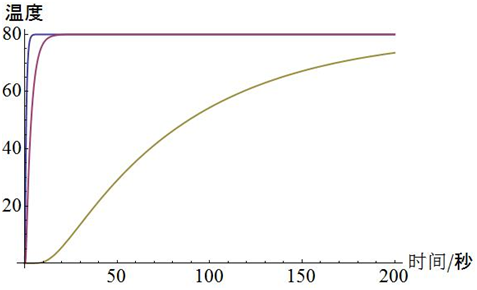
由模型可知,薄肉片更容易加热
可以看到,比较薄的肉片放到热汤几秒钟的时间就会达到和汤几乎一致的温度,而比较厚的肉片中心需要很长的时间才能够热起来,对于米线来说,汤可能早就凉了,因此较厚的肉片中心也就并不能达到较高的温度。而这个“很长的时间”可以从前面给出的解中估计出来。如果肉片的厚度是 L(毫米),则需要数个 L 2 秒的时间才能把肉片的中心加热到汤的温度。吃过小肥羊或者海底捞、涮过羊肉的读者应该在生活里面做过实验的验证了。
至此,根据上面的分析可知,比较薄的肉片(毫米厚度)在数秒之内就可以加热到汤的温度,而这个时间内汤基本不会变凉。
但如果肉片比较厚,或者互相叠放(相当于增加了肉片的厚度),那就会需要很长时间的加热,肉片中心才能够达到杀死旋毛虫的温度,而在这段时间里,汤则会因为加入其他的材料以及热量散失等原因变凉。如果肉本身带有旋毛虫的话,食用起来恐怕就会有感染的风险。所以这里也建议大家把肉片放到汤里面的时候把肉片分开一些,不要叠放在一起。
两点补充说明
实际上,为了方便建模运算,我们做了两点假设。
- 我们假设在肉片升温的过程中汤的温度不变。实际情况下,汤在把热传递给肉片时温度会降低,随着时间的变化,汤会变凉。但对于比较薄的肉片,加热时间远小于汤温度明显降低所需的时间,因此假设是合理的。而对于较厚的肉片,需要较长的加热时间,所以在实际的情况中,加热需要的时间会比我们计算的结果要更长一些。
- 我们用水的热扩散系数代替了肉片里的扩散系数。这是由于肉里面绝大部分都是水,含有的蛋白质和脂肪等有机物虽会影响肉片的传导系数,但影响程度不大。哈佛大学应用数学和应用物理系的 Michael Brenner 教授曾经在一个科普讲座里面用金枪鱼块测量了水的热扩散系数,得出了很准确的数字[3]。如果把肉片换成导热性更差的木头(其热扩散系数略大于水的一半[2]),加热时间会大约是原来的 2 倍。也就是说,即使是1mm厚的木片插到汤里面的话, 5 ~ 6 秒钟后木片中心就应该跟汤的温度基本一致了。
本文用模型揭示了这样一个事实:肉片的厚度会导致内部温度上升时间的极大延长。但因为这只是理论上的计算,而实际生活中存在很多变量,所以最后还请以相关标准为指导。死理性派提醒大家,根据《云南省旋毛虫病公共卫生应急预案(试行)》的建议,在吃过桥米线时最好能将肉片在 85℃ 的汤中浸烫 1 - 2 分钟。
参考资料:
| [1] | 维基百科: heat equation |
| [2] | (1, 2) 维基百科: Thermal diffusivity |
| [3] | Boulder Summer School 2011, Public lecture “Science and Cooking”. |
附推导过程:
