BK-Tree算法（模糊匹配）

转自： http://www.matrix67.com/blog/archives/333

除了字符串匹配、查找回文串、查找重复子串等经典问题以外，日常生活中我们还会遇到其它一些怪异的字符串问题。比如，有时我们需要知道给定的两个字 符串“有多像”，换句话说两个字符串的相似度是多少。1965年，俄国科学家VladimirLevenshtein给字符串相似度做出了一个明确的定义 叫做Levenshtein距离，我们通常叫它“编辑距离”。字符串A到B的编辑距离是指，只用插入、删除和替换三种操作，最少需要多少步可以把A变成 B。例如，从FAME到GATE需要两步（两次替换），从GAME到ACM则需要三步（删除G和E再添加C）。Levenshtein给出了编辑距离的一 般求法，就是大家都非常熟悉的经典动态规划问题。

    在自然语言处理中，这个概念非常重要，例如我们可以根据这个定义开发出一套半自动的校对系统：查找出一篇文章里所有不在字典里的单词，然后对于每个单词， 列出字典里与它的Levenshtein距离小于某个数n的单词，让用户选择正确的那一个。n通常取到2或者3，或者更好地，取该单词长度的1/4等等。 这个想法倒不错，但算法的效率成了新的难题：查字典好办，建一个Trie树即可；但怎样才能快速在字典里找出最相近的单词呢？这个问题难就难 在，Levenshtein的定义可以是单词任意位置上的操作，似乎不遍历字典是不可能完成的。现在很多软件都有拼写检查的功能，提出更正建议的速度是很 快的。它们到底是怎么做的呢？1973年，Burkhard和Keller提出的BK树有效地解决了这个问题。这个数据结构强就强在，它初步解决了一个看 似不可能的问题，而其原理非常简单。

    首先，我们观察Levenshtein距离的性质。令d(x,y)表示字符串x到y的Levenshtein距离，那么显然：

1. d(x,y) = 0 当且仅当 x=y  （Levenshtein距离为0 <==> 字符串相等）

2. d(x,y) = d(y,x)     （从x变到y的最少步数就是从y变到x的最少步数）

3. d(x,y) + d(y,z) >= d(x,z)  （从x变到z所需的步数不会超过x先变成y再变成z的步数）

    最后这一个性质叫做三角形不等式。就好像一个三角形一样，两边之和必然大于第三边。给某个集合内的元素定义一个二元的“距离函数”，如果这个距离函数同时 满足上面说的三个性质，我们就称它为“度量空间”。我们的三维空间就是一个典型的度量空间，它的距离函数就是点对的直线距离。度量空间还有很多，比如 Manhattan距离，图论中的最短路，当然还有这里提到的Levenshtein距离。就好像并查集对所有等价关系都适用一样，BK树可以用于任何一 个度量空间。

    建树的过程有些类似于Trie。首先我们随便找一个单词作为根（比如GAME）。以后插入一个单词时首先计算单词与根的Levenshtein距离：如果 这个距离值是该节点处头一次出现，建立一个新的儿子节点；否则沿着对应的边递归下去。例如，我们插入单词FAME，它与GAME的距离为1，于是新建一个 儿子，连一条标号为1的边；下一次插入GAIN，算得它与GAME的距离为2，于是放在编号为2的边下。再下次我们插入GATE，它与GAME距离为1， 于是沿着那条编号为1的边下去，递归地插入到FAME所在子树；GATE与FAME的距离为2，于是把GATE放在FAME节点下，边的编号为2。

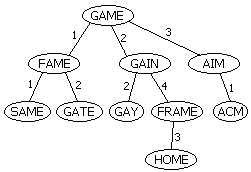
    查询操作异常方便。如果我们需要返回与错误单词距离不超过n的单词，这个错误单词与树根所对应的单词距离为d，那么接下来我们只需要递归地考虑编号在d-n到d+n范围内的边所连接的子树。由于n通常很小，因此每次与某个节点进行比较时都可以排除很多子树。

    举个例子，假如我们输入一个GAIE，程序发现它不在字典中。现在，我们想返回字典中所有与GAIE距离为1的单词。我们首先将GAIE与树根进行比较， 得到的距离d=1。由于Levenshtein距离满足三角形不等式，因此现在所有离GAME距离超过2的单词全部可以排除了。比如，以AIM为根的子树 到GAME的距离都是3，而GAME和GAIE之间的距离是1，那么AIM及其子树到GAIE的距离至少都是2。于是，现在程序只需要沿着标号范围在 1-1到1+1里的边继续走下去。我们继续计算GAIE和FAME的距离，发现它为2，于是继续沿标号在1和3之间的边前进。遍历结束后回到GAME的第 二个节点，发现GAIE和GAIN距离为1，输出GAIN并继续沿编号为1或2的边递归下去（那条编号为4的边连接的子树又被排除掉了）……

    实践表明，一次查询所遍历的节点不会超过所有节点的5%到8%，两次查询则一般不会17-25%，效率远远超过暴力枚举。适当进行缓存，减小Levenshtein距离常数n可以使算法效率更高。