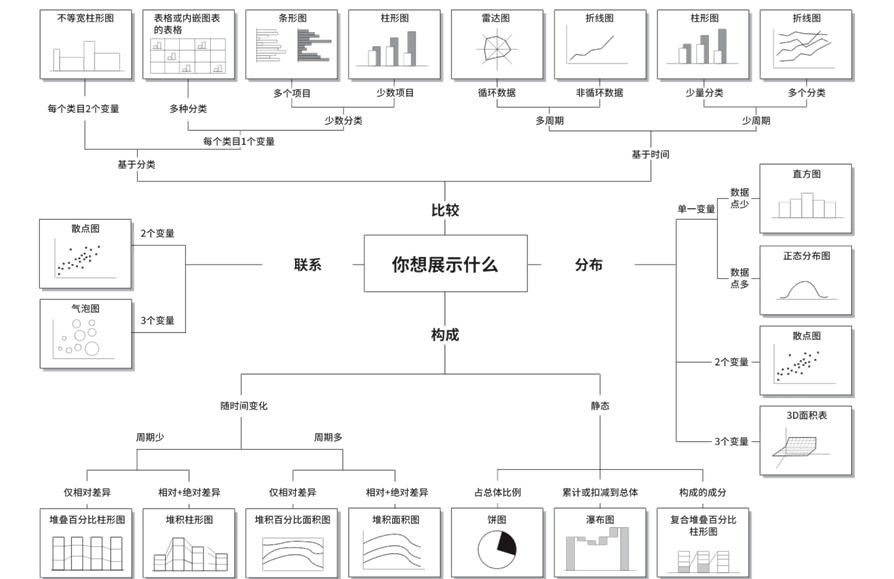
探索性数据分析详解

什么是探索性数据分析？

探索性数据分析（Exploratory Data Analysis，简称EDA） 是指对已有的数据（特别是调查或观察得来的原始数据）在尽量少的先验假定下进行探索，通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。

探索性数据分析（EDA）与传统统计分析（Classical Analysis）的区别：

• 传统的统计分析方法通常是先假设样本服从某种分布，然后把数据套入假设模型再做分析。但由于多数数据并不能满足假设的分布，因此，传统统计分析结果常常不能让人满意。
• 探索性数据分析方法注重数据的真实分布，强调数据的可视化，使分析者能一目了然看出数据中隐含的规律，从而得到启发，以此帮助分析者找到适合数据的模型。“探索性”是指分析者对待解问题的理解会随着研究的深入不断变化。

探索性数据分析除了日常的数据分析外，也是算法模型搭建过程中的必要环节。特别适合数据比较杂乱，不知所措的场景。

探索性分析用一句话概况就是：折磨数据，它会坦白任何事情。

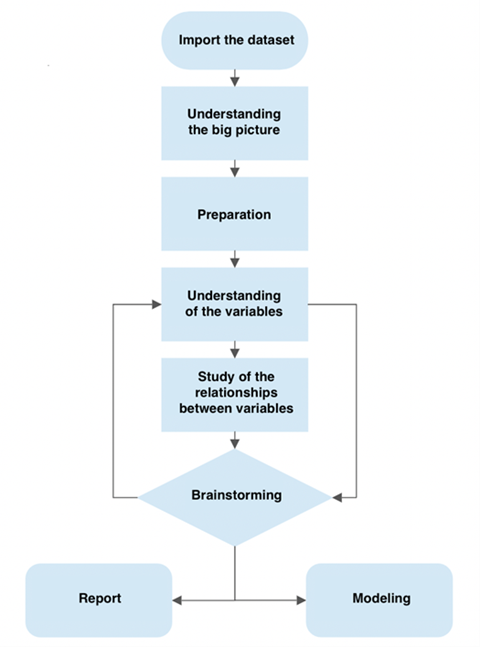
探索性数据分析的一般流程

探索性分析的一般流程：

• 数据总览
• 探索性分析每个变量
• 探索性分析变量与target标签的关系
• 探索性分析变量之间的关系

数据总览

在数据处理前首先要充分了解数据，了解数据包含以下两部分：

• 了解数据的外部信息。即数据的现实意义。可通过业务知识与流量计获取采集方式进行了解。
• 了解数据的内部信息。即数据的自身情况。可通过统计学的相关知识，如计算均值，标准差，峰度，偏度等。另外，也可以通过绘图，来深入了解数据，为创建有效特征提供思路。

对于数据总览一般可借助Pandas的一些函数对数据有些大概了解：

• describe() # 查看所有数据平均值，四分位数等信息
• info() # 查看所有数据的数据类型和非空值个数。
• shape # 查看数据行列数
• isnull().sum() # 查看数据各个特征为空值的个数

探索性分析每个变量

需要了解的内容包括：

• 变量是什么类型
• 变量是否有缺失值
• 变量是否有异常值
• 变量是否有重复值
• 变量是否均匀
• 变量是否需要转换
• …

在分析每个变量可通过描述统计量和图表进行描述。数据类型分为数值型，类别型，文本型，时间序列等。这里主要指的是数值型（定量数据）和类别型（定性数据），其中数值型又可以分为连续型和离散型。

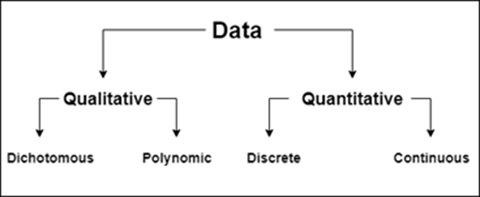
1）连续数据分析

数据分析分为两个方面，一是统计汇总，二是可视化。离散也是这样。

统计计算：

• 在统计学中，想要描述一个数据，要从三个方面进行说明：
  • 集中趋势：均值，中位数，众数。对于正太分布的数据，均值的效果比较好，而对于有偏数据，因为存在极值，所有会对均值产生影响，此时，用中位数去进行集中趋势的描述。
  • 离散程度：方差和标准差。这两个用哪个都可，不过标准差是具有实际意义的。另外，还可以用极差，平均差，四分位差，离散系数（针对多组数据离散程度的对比）。
  • 分布形状：偏度skew()，衡量数据偏斜情况。峰度kurt()，衡量数据分布的平坦度。检验数据正态性。一般可绘制P-P图，Q-Q图来进行判断。或者通过计算偏度，峰度进行判断，也有其他别的方法，但了解的较少。
• 数据转化。这步一般在特征工程中，这里提一下，通过box-cox可以将非正态数据转为正态数据。
• 游程检验。非参数统计的一种方法，判断数据是否是随机出现的。连续，离散都可以用。
• 通过describe()，可观察数据的大致情况。

可视化：

• 对连续数据可视化主要有以下几个图形：
  • 直方图。可以大致看出数据的分布情况，但会受限于bins的取值并且图形不光滑。可在直方图上再画出核密度图(KDE)，进行更详细的查看。
  • 核密度估计
  • 核密度图
  • 箱线图。反映原始数据的分布特征，还能进行多组数据的比较。可看出数据的离群点。
  • 散点图。利用索引和连续数据作散点图，直观看数据是否随机。
• 类型转换
  • 将连续型数据转为离散型数据。比如，年龄，可以将其分组为少年，青年，壮年，老年等。这种处理方式的关键是如何分组，在数据噪声处理中有过描述，介绍了人为区分，等深等宽分组，无监督算法分组，聚类等方法。
  • 关于为什么要把连续型数据转为离散型数据，大概的好处有：去噪声，易理解，算法需要。

针对连续变量常见的描述统计量：平均值，中位数，众数，最小值，最大值，四分位数，标准差等

图表：频数分布表（需进行分箱操作），直方图，箱形图（查看分布情况）

2）离散数据分析

统计计算

• 主要查看数据的结构。用众数看哪类数据出现的最多。利用value_counts()函数，查看各个类别出现的次数。

可视化

• 饼图。对于查看数据结构比较直观，所占百分比。
• 柱形图。对各类别出现次数进行可视化。可排序，这样观察数据更直观。

针对 无序型离散变量常见的描述统计量：各个变量出现的频数和占比

图表：频数分布表（绝对频数，相对频数，百分数频数），柱形图，条形图，茎叶图，饼图

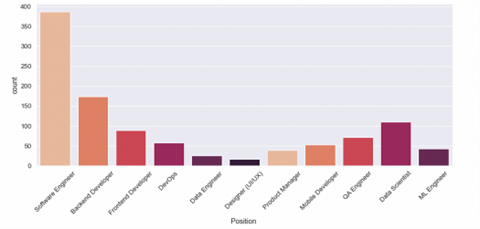
针对 有序型离散变量常见的描述统计量：各个变量出现的频数和占比

图表：频数分布表，堆积柱形图，堆积条形图（比较大小）

变量间关系分析

当对单个数据分析完后，还要看各个数据与目标特征的关系，和除目标特征外，其他数据间的关系。

• 探索性分析变量与target标签的关系
• 探索性分析变量之间的关系

1）连续型变量与连续型变量关系

统计计算：

• 协方差，可以得到两个变量间的相关性。但协方差越大，并不表明越相关。因为协方差的定义中没有考虑属性值本身大小的影响。
• 相关系数考虑了属性值本身大小的影响，因此是一个更合适的统计量。取值在[-1,1]上，-1表示负相关，即变换相反，1表示正相关，0则表示不相关。相关系数是序数型的，只能比较相关程度大小(绝对值比较),并不能做四则运算。而相关系数一般常用的有三种：
  • Pearson相关系数：这个比较常用，主要用于正态的连续型数据间的比较。但在使用时，限制的条件比较多，对于偏态数据，效果不是很好。
  • Spearman相关系数：相比于Pearson，这个的限制条件比较少，不受异常值影响。可以应用在多种场合。但若对正太正态数据使用，则效果一般。
  • Kendall相关系数：限制条件同Spearman。一般用在分类数据的相关性上。
  • 注：Pearson和协方差，主要看数据间的关系是不是线性的，如不是线性，但有其他联系，这两个系数是判断不出来的。比如指数函数这种。而Spearman和Kendall则可以进行一定的判断，主要是单调增函数。

可视化

• 散点图。可看出两个特征间的关系大致是什么样的。如果要具体探究数据间的关系，需要进行一定的计算。
• 相关性热力图。如果是一个数据与另一个时间序列进行搭配，则这个图可以很好地看出变化趋势。

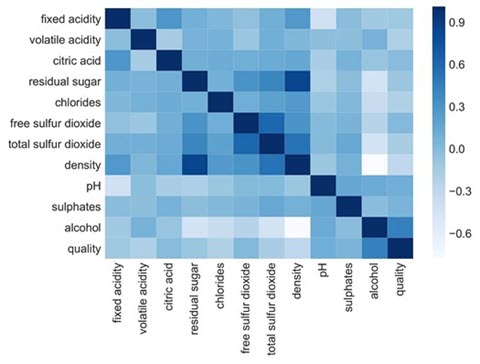
对于连续变量与连续变量之间的关系，可以通过散点图进行查看。对于多个连续变量，可使用散点图矩阵，相关系数矩阵，热图。

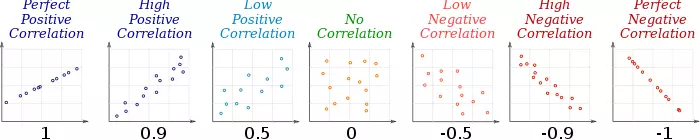
量化指标：皮尔逊相关系数（线性关系），互信息（非线性关系）

2）离散变量和离散变量关系

对于离散变量与离散变量之间的关系，可以通过交叉分组表（crosstab），复合柱形图，堆积柱形图，饼图进行查看。对于多个离散变量，可以使用网状图，通过各个要素之间是否有线条，以及线条的粗线来显示是否有关系以及关系的强弱。

量化指标：卡方独立性检验—>Cramer’s φ (Phi) or Cramer’s V

3）离散变量和连续变量关系

对于离散变量和连续变量之间的关系，可以使用直方图，箱线图，小提琴图进行查看，将离散变量在图形中用不同的颜色显示，来直观地观察变量之间的关系。

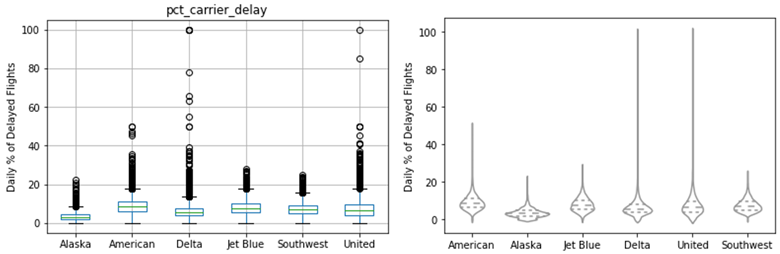
量化指标：独立样本t检验中的t统计量和相应的p值（两个变量），单因素方差分析中的η²（三个变量及以上）

4） 其他

检查数据的正态性：直方图，箱线图，Q-Q图（Quantile-Quantile Plot ）

• 直方图，箱线图：看图形是否对称
• Q-Q图：比较数据的分位数与某个理论分布的分位数是否匹配

探索性数据分析的的产出

根据EDA我们可以得出以下结论：

• 变量是否需要筛选、替换和清洗
• 变量是否需要转换
• 变量之间是否需要交叉
• 变量是否需要采样

探索性数据分析的辅助工具

• DataPrep
• Pandas Profiling
• Sweetviz
• AutoViz
• Klib
• Dabl
• SpeedML

参考链接：

• Exploratory Data Analysis in Python — A Step-by-Step Process
• Advanced exploratory data analysis (EDA) with Python
• 10 automated EDA libraries in one place | by Satyam Kumar | Geek Culture | Medium

其他参考：