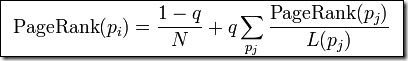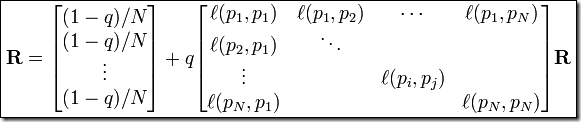Google矩阵

文章系本人原创，转载请保持完整性并注明出自 《四火的唠叨》

使用一款搜索引擎，我们希望搜索结果能够拥有最佳的排序，Google为它最核心的排序算法PageRank申请了专利。在PageRank以前，排序大多依靠对搜索关键字和目标页的匹配度来进行的，这种排序方式弊端明显，尤其对于善于堆砌关键字舞弊的页面，很容易就跳到了搜索结果的首页。Larry Page和Sergey Brin开始着手解决这个问题，Google排序的继承来自于互联网上网页之间的链接关系。一张网页被其它网页引用的次数越多，可以简单地认为这样的网页越受欢迎，当然在结果列表中应该越靠前。

前面提到了目标网页被引用网页的“数量”，另一条重要的判定PageRank级别的依据则是“质量”。换言之，质量高的网页所引用的网页，质量往往也比较高，所以质量高的网页投票所占权重理应更高。

在用户访问某一张网页时，假设他有q的概率去点击网页上的链接，并且点击该网页每条链接的概率都是相等的。如果该网页有n条链接的话，那么点击每条链接的概率就是1/n。

在表现网页之间链接关系时，Google使用了矩阵。假设互联网上共有N个页面，那么我们可以写出一个N×N的矩阵，其中的元素p _ij，如果存在从页i被页j指向的链接（为什么使用“被指向”而非“指向”，前文已经解释了），那么p _ij就大于0，反之就等于0。同时，每一列元素的取值都除以链接数n（前文提到了），使得各列矢量总和成为1，行矢量则表示了各个状态之间的迁移概率，这个最大特征值为1的矩阵就成为了PageRank矩阵。

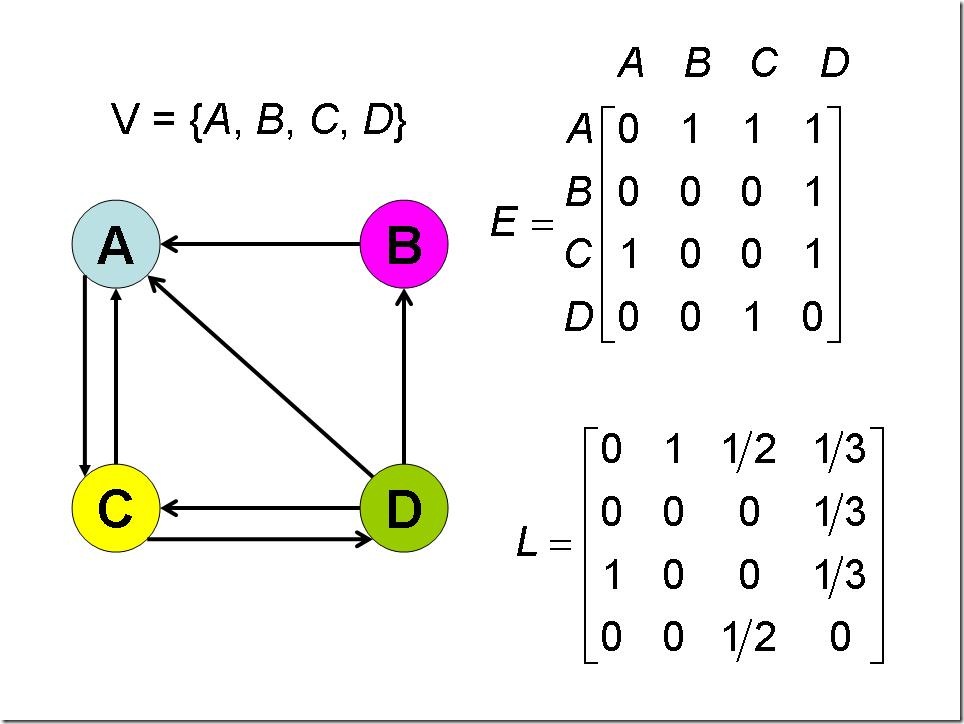
现在给出N为4的一个例子（共有A、B、C、D四张网页）帮助说明这个矩阵（这个例子来自于 这篇文章）：

可以看到矩阵L的几个非零元素的取值：

• p ₁₃=1; 表示被A指向的只有C
• p ₁₂=1; 表示被B指向的只有A
• p ₁₃=p ₄₃=1/2; 表示被C指向的有A和D
• p ₁₄=p ₂₄=p ₃₄=1/3; 表示被D指向的有A、B、C

于是，对于A来说，它的PageRank取值就可以表示为：

PR(A) = PR(B)/1 + PR(C)/2 + PR(D)/3

但这是在用户百分之百点击网页链接的情况下发生的，实际上，只有p概率的用户会点击网页链接，剩下(1-p)概率的用户会跳到无关的页面上去，而访问的页面恰好是4这个页面中A的概率只有(1-p)/4（p正是前文提到的“阻尼系数”（damping factor），Google取p等于0.85），所以：

PR(A) = (1-p)/4 + p(PR(B)/1 + PR(C)/2 + PR(D)/3)

推广到一般公式（p _i表示第i张网页，L(p _j)表示从p _i链出网页的数量）：

有了PageRank(p _i)的概念以后，PageRank矩阵就可以用一个特征向量来表示：

由上述两个公式，可以得到（其中l(p _i,p _j)就是前文提到过的p _{i j}）：

以上未特殊注明的公式截图来自于维基百科。

截止到2010年，Google索引的网页总数已经超过5000亿，也就是说，Google必须解这个阶数的特征向量，这个过程我不得而知，但这是不是真的就是MapReduce之类的由来呢？

文章系本人原创，转载请保持完整性并注明出自 《四火的唠叨》

• 从“Google地图八位版”看国内的抄袭