趣题：能否在等边三角形点阵中画一个正方形？
- 刚子 - Matrix67: My Blog 这是一个非常有趣的问题：能否在一个无限大的等边三角形点阵中选取四个点，使得这四个点恰好构成一个正方形. 这个问题有一个非常简单巧妙的解法，你能想到吗. 为了证明这一点，首先注意到，如果选定三角形点阵中任意两个不同的点，则以这两个点为顶点作等边三角形，所得的第三个顶点也一定在点阵中. 这是因为，以任意一点为中心，将整个平面旋转 60 度，新的点阵与原来的点阵仍然是重合的.
趣题：能否在等边三角形点阵中画一个正方形？
标签：
趣题
Brain
Storm
几何
证明
| 发表时间：2011-08-08 21:58 | 作者：Matrix67 刚子
出处：http://www.matrix67.com/blog
这是一个非常有趣的问题：能否在一个无限大的等边三角形点阵中选取四个点，使得这四个点恰好构成一个正方形？这个问题有一个非常简单巧妙的解法，你能想到吗？
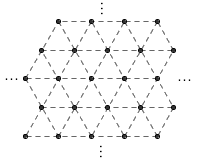
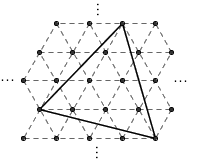
答案：不可能。为了证明这一点，首先注意到，如果选定三角形点阵中任意两个不同的点，则以这两个点为顶点作等边三角形，所得的第三个顶点也一定在点阵中。这是因为，以任意一点为中心，将整个平面旋转 60 度，新的点阵与原来的点阵仍然是重合的。等边三角形的第三个顶点，其实可以看作是已知两点中的其中一点绕另一点旋转 60 度所得的，自然也就还在点阵中了。
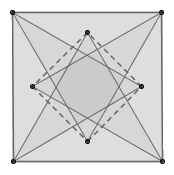
下面，假设点阵中存在正方形，则我们一定能找到一个最小的正方形。以正方形的每条边为边，向内作等边三角形，所得的第三个顶点也仍然在点阵上。然而，这四个新的顶点将会构成一个更小的正方形，于是产生矛盾。所以，我们永远无法在等边三角形点阵中作出一个正方形来。
题目来源：http://www.cut-the-knot.org/Curriculum/Geometry/DavidRadcliffe.shtml
大家有什么其他的证明方法吗？
相关 [趣题 三角形 点阵] 推荐：
CSS quiz: 带边 border 的三角形
- - 幸福收藏夹在 twitter 上发了一条推，给一道 CSS 题给大家做. 有几位同学给了回答，@zhiyelee 同学还给出了他的 具体实现方案. 推的原文是：“CSS Quiz: 如何不用图片、兼容所有浏览器实现这样的界面. 晚上博客公布答案 twitpic.com/981xba”. 如 @zhiyelee 同学的方案所示，原理可以分解为：.
经典证明：等边三角形内一点到各顶点的距离长可构成一个三角形
- Andy - Matrix67: My Blog 这是初中平面几何的一个经典问题：等边三角形 ABC 内有任意一点 P，求证 PA 、 PB 、 PC 的长度一定能构成一个三角形. 这里给出两种证明方法. 传统的证明方法是，把 △CPA 绕着点 C 逆时针旋转 60 度，从而旋转后的 CA 将会和 CB 重合，同时 P 点落在了 P' 的位置.
终于搞懂了CSS实现三角形图标的原理
- - ITeye博客网页中经常有一种三角形的图标，鼠标点一下会弹出一个下拉菜单之类的（之前淘宝也有，不过现在改版好像没有了）. 之前以为是个png图标背景，后来在bootstrap中看到有一个图标样式叫做caret的用来实现这种效果. 没想到用CSS也能实现这个效果. .caret {
display: inline-block;
width: 0;
height: 0;
margin-left: 2px;
vertical-align: middle;
border-top: 4px solid;
border-right: 4px solid transparent;
border-left: 4px solid transparent;
}.
趣题：不用相似怎么办？
- flycondor - Matrix67: My Blog 我老早就写过一个经典的小学几何题. 如果你还没看过这个问题，你一定要去看看. 一个小学奥数老师曾经告诉我，当年带领学生参加这次竞赛时，领队老师们都没有想到这个问题的“小学生解法”，以至于开始质疑这道题是否超纲了. 看到答案后，老师们大为折服——这个问题确实有一个无需任何几何知识的妙解. 今天，同样的事情发生了.
44个精彩的物理趣题
- Henry - Matrix67: My Blog 这个 Blog 几乎一直在讲数学趣题，却很少提到物理趣题. 其实，我个人觉得，物理也是相当好玩的（我是化学不好才选的文科）. 隐约记得初中搞物理竞赛时，曾见过大量让人大呼过瘾的好题. 前几天看到了一个绝好的网站，里面有相当多的物理题目，让我激动了好一阵子. 我搜集整理了里面的一些好题，加上了我自己的一些补充，在这里和大家分享.
趣题：不动点与线性代数
- sdyy1990 - Matrix67: My Blog 假设 X 、 Y 是两个有限集合，f:X→Y 和 g:Y→X 是两个函数. 求证：复合函数 g∘f 和 f∘g 拥有相同数量的不动点（也就是说 g(f(x)) = x 和 f(g(y)) = y 的解的个数相同）. 下面先提供一个“正常”的解法. 观察函数 g∘f 的不动点，可以看出它有以下两个性质：首先，如果某个 x 是 g∘f 的不动点，即 x = g(f(x)) ，那么 f(x) = f(g(f(x)))，这就说明 f(x) 是 f∘g 的一个不动点；另外，如果 x1 和 x2 是 X 中两个不同的不动点，则函数 f 不可能把它们映射到 Y 中的同一个元素，否则 g 没办法把它分别还原成 x1 和 x2.
趣题：随机折断的木棒
- Wang - FeedzShare来自: Matrix67: My Blog - FeedzShare . 发布时间:2011年02月06日, 已有 3 人推荐. 随机在中间选取一点，把这根木棒折断. 那么，短的那一截木棒平均有多长. 随机在中间选取一点，把这根木棒折断. 那么，长的那一截木棒平均有多长. 随机在中间选取一点，把这根木棒折断.
趣题：不用相似怎么办？
- 法法 - Matrix67: My Blog 我老早就写过一个经典的小学几何题. 如果你还没看过这个问题，你一定要去看看. 一个小学奥数老师曾经告诉我，当年带领学生参加这次竞赛时，领队老师们都没有想到这个问题的“小学生解法”，以至于开始质疑这道题是否超纲了. 看到答案后，老师们大为折服——这个问题确实有一个无需任何几何知识的妙解. 今天，同样的事情发生了.
趣题：舞台里的狮子
- Dajusha - Matrix67: My Blog 有一个半径为 10 米的圆形舞台，初始时舞台上的某个地方有一头狮子. 这头狮子在舞台上以折线段的方式跑了 30 千米. 求证：在整个过程中，这头狮子至少转了 2998 个弧度. 有时候，换一个角度思考，问题就会迎刃而解. 现在，让我们站在狮子的角度，用狮子的眼光来看周围的世界.