IMO2011趣题：总存在一条将会遍历所有点的直线

    下面这个精彩的问题来自于刚刚结束的 IMO 2011 中的第 2 题：

    设 S 是平面上包含至少两个点的一个有限点集，其中没有三点在同一条直线上。所谓一个“风车”是指这样一个过程：从经过 S 中单独一点 P 的一条直线 l 开始，以 P 为旋转中心顺时针旋转，直至首次遇到 S 中的另一点，记为点 Q 。接着这条直线以 Q 为新的旋转中心顺时针旋转，直到再次遇到 S 中的某一点，这样的过程无限持续下去。
    证明：可以适当选取 S 中的一点 P ，以及过 P 的一条直线 l ，使得由此产生的“风车”将 S 中的每一点都无限多次用作旋转中心。

    注意，由于两点确定的直线只有有限多条，因此直线无限旋转下去，必然会出现和以前某个时刻相同的状态，于是产生循环。另外，由于直线旋转的过程是可逆的，我们不必担心最终产生的是一个 ρ 字形的循环。因此，我们实际上只需要证明，存在这样一条初始直线，它可以碰到所有的点。

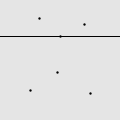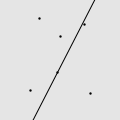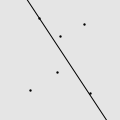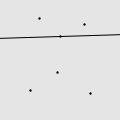
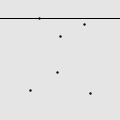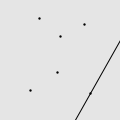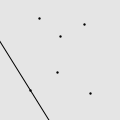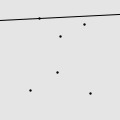
    我用 Mathematica 写了一个程序，做了一些直观的动画。如图所示的由 6 个点构成的点集，适当地选择初始直线就能遍历所有的点，但错误的选择将会导致有一些点永远也碰不到。

    IMO 2011 赛后统计资料显示，这道漂亮的问题竟然是六道题中第二难的题（第一难的题是最后一道）。 polymath blog 组织了 mini-polymath3 活动，邀请众人一同讨论这道题的解法。活动一开始，便引来各路数学高人献计献策，提出了很多有趣的思路和猜想；第 74 分钟，终于有人给出了正确的解法。果然不出所料，神题就该有神解，这道题有一个异常简单巧妙的证明方法。

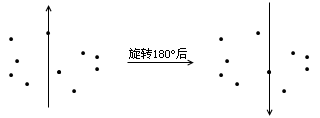
    找一条直线，这条直线两侧的点数一样多（最多相差一个）。下面我们证明，这条直线就满足要求。容易看出，在直线的旋转过程中，直线两侧的点数之差始终不变。因此，这条直线转了 180 度后，直线一定回到了初始的位置（或者它旁边一个点的位置）。但此时，原来在直线左侧的点现在全部跑到了直线右侧，原来在直线右侧的点现在全部跑到了直线左侧。这些点当然是不能瞬移到直线另一侧的，要想跑到直线的另一侧，必须要先穿过直线才行。由此可见，所有点都被直线碰到过了。